Требования к оформлению контрольной работы
В процессе изучения курса математики студент должен выполнить в каждом семестре одну контрольную работу. Контрольная работа № 3 состоит из 8 заданий (11 задач) для каждого варианта. Студент решает один из десяти вариантов. Номер варианта определяется по последней цифре номера студенческого билета или зачетной книжки (если последняя цифра 0, то необходимо решить задачи 10 варианта).
При выполнении контрольных работ нужно придерживаться следующих правил.
1. Каждую контрольную работу следует выполнять в отдельной тонкой тетради в клетку (не более 24 листов), оставляя поля для замечаний рецензента.
2. На обложке тетради необходимо указать: а) свою фамилию и инициалы; б) институт; в) номер группы; г) номер зачетной книжки; д) номер контрольной работы; е) название дисциплины (см. приложение).
Помимо общих данных на титульном листе печатается матрица учета задач.
| 1.1 | 1.2 | 1.3 | 2.1 | 2.2 | 3.1 | 3.2. | 3.3. | |||
| а | б | а | б | в | ||||||
Отметку о правильном выполнении задачи (+) ставит преподаватель.
ВНИМАНИЕ!!! При отсутствии правильно оформленного титульного листа (особенно, если помимо ФИО студента не указаны номера его группы и зачетной книжки) КОНТРОЛЬНАЯ РАБОТА НЕ ПРОВЕРЯЕТСЯ!
3. В контрольную работу должны быть включены все задачи, указанные в задании, и в строгом соответствии с номером своего варианта.
|
|
|
4. Решения задач в каждой контрольной работе следует располагать обязательно в порядке номеров, указанных в задании (см. матрицу учета задач).
5. Оформление решения каждой задачи должно обязательно включать в себя запись условия задачи в начале и ответ (отдельно выделенной строкой) в конце.
6. Решения задач должны содержать подробные пояснения и необходимые рисунки. Все решения и рисунки выполняются от руки. Использование онлайн-калькуляторов разрешается только для проверки правильности Вашего решения. В случае прямого копирования работы онлайн-калькулятора решение задачи не засчитывается.
7. После получения прорецензированной работы студент должен исправить все отмеченные рецензентом замечания и недочеты, а также выполнить все его рекомендации. Исправления нужно записывать в этой же тетради после всех решенных задач контрольной работы. Вносить исправления в тексты решения задач после рецензирования запрещается.
Незачтенную контрольную работу с последующими соответствующими исправлениями следует направить на повторную рецензию.
8. Контрольная работа в каждом семестре должна быть представлена для рецензирования не позднее, чем за 2 недели до начала экзаменационной сессии. Рецензирование контрольных работ, переданных на проверку позже указанного срока, переносится на начало следующего семестра.
|
|
|
Контрольная работа считается зачтенной при наличии всех правильно выполненных задач (на титульном листе ставится соответствующая отметка).
Прорецензированную и зачтенную контрольную работу студент должен предъявлять экзаменатору перед сдачей зачета или экзамена.
Решение нулевого варианта
Раздел 1. Числовые и степенные ряды
Задание 1.1. Пользуясь необходимым признаком сходимости числовых рядов, доказать, что 
Теоретический минимум
_____________________________________________
Выражение вида 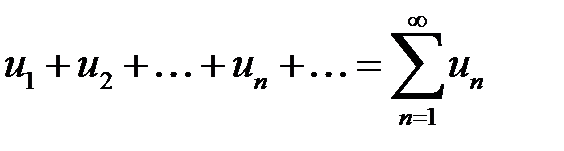 называется числовым рядом.
называется числовым рядом.
Сумма первых n слагаемых называется n-ной частичной суммой числового ряда и обозначается 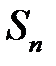 .
.
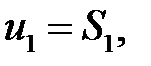
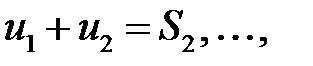

При этом  − действительные или комплексные числа, называемые членами ряда, где
− действительные или комплексные числа, называемые членами ряда, где  − общий член ряда.
− общий член ряда.
Если предел последовательности частичных сумм ряда 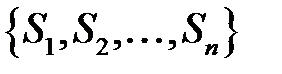 равен конечному числу
равен конечному числу 
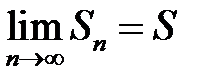 , то ряд называют сходящимся , где
, то ряд называют сходящимся , где 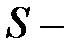 сумма ряда, если нет – то ряд расходящийся, он не имеет конечной суммы.
сумма ряда, если нет – то ряд расходящийся, он не имеет конечной суммы.
Необходимый признак сходимости числового ряда: если числовой ряд  сходится, то предел общего члена ряда равен нулю
сходится, то предел общего члена ряда равен нулю 
|
|
|
Необходимый признак сходимости не верен в обратную сторону, то есть из стремления общего члена ряда к нулю не следует его сходимость!
Для проверки сходимости знакоположительных рядов (рядов с общим членом 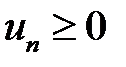 ) используют достаточные признаки сходимости:
) используют достаточные признаки сходимости:
1. Первый признак сравнения. Пусть ряды 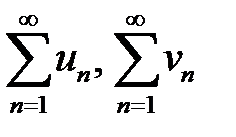 ‑ знакоположительные и
‑ знакоположительные и  Если сходится ряд с большим общим членом ряда
Если сходится ряд с большим общим членом ряда 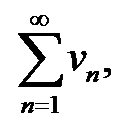 то сходится и с меньшим
то сходится и с меньшим  Если расходится ряд с меньшим общим членом ряда
Если расходится ряд с меньшим общим членом ряда  то расходится и с большим
то расходится и с большим 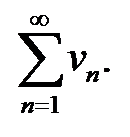
2. Второй (предельный) признак сравнения. Пусть ряды 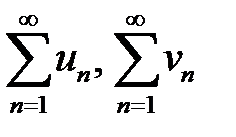 ‑ знакоположительные и
‑ знакоположительные и  если с – конечное число, отличное от нуля, то ряды сходятся и расходятся одновременно.
если с – конечное число, отличное от нуля, то ряды сходятся и расходятся одновременно.
3. Признак Даламбера. Пусть ряд 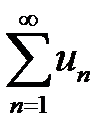 ‑ знакоположительный и
‑ знакоположительный и  ‑ конечное число. Если
‑ конечное число. Если 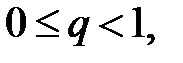 то ряд сходится; если
то ряд сходится; если  то ряд расходится; если
то ряд расходится; если 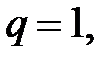 то признак Даламбера не дает ответа на вопрос о сходимости ряда.
то признак Даламбера не дает ответа на вопрос о сходимости ряда.
4. Радикальный признак Коши. Пусть ряд 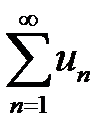 ‑ знакоположительный и
‑ знакоположительный и 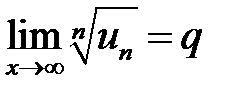 ‑ конечное число. Если
‑ конечное число. Если 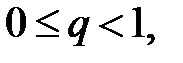 то ряд сходится; если
то ряд сходится; если  то ряд расходится; если
то ряд расходится; если 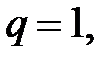 то признак Коши не дает ответа на вопрос о сходимости ряда.
то признак Коши не дает ответа на вопрос о сходимости ряда.
5. Интегральный признак Коши. Пусть члены знакоположительного ряда 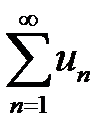 являются значениями некоторой монотонно убывающей функции на промежутке
являются значениями некоторой монотонно убывающей функции на промежутке 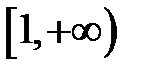 функции
функции 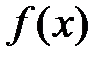 так, что
так, что 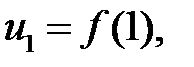
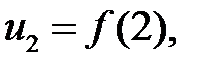 …,
…, 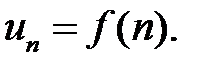 Тогда
Тогда
|
|
|
1) если 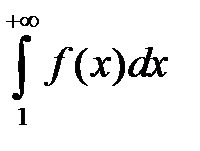 сходится, то сходится и ряд
сходится, то сходится и ряд 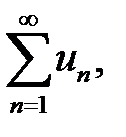
2) если 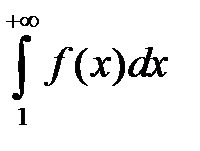 расходится, то расходится и ряд
расходится, то расходится и ряд 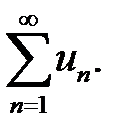
Для признаков сравнения используют ряды вида
1) 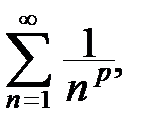 который сходится при
который сходится при  и расходится при
и расходится при 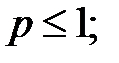
2)  который сходится при
который сходится при  и расходится при
и расходится при 
_______________________________________________________________
Решение:
Условие 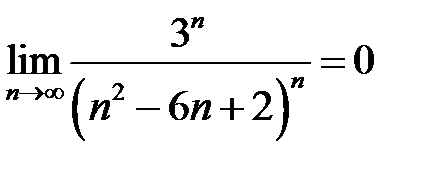 является необходимым признаком для сходимости ряда
является необходимым признаком для сходимости ряда  Для доказательства его сходимости применим радикальный признак Коши:
Для доказательства его сходимости применим радикальный признак Коши: 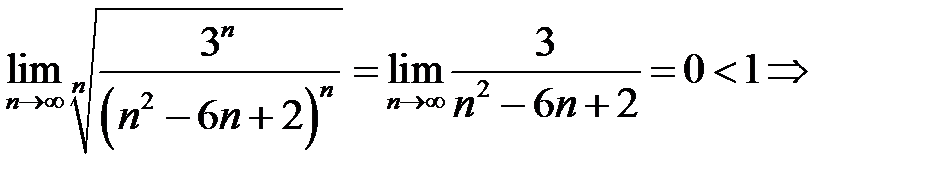 ряд сходится.
ряд сходится.
Из сходимости ряда  следует, что
следует, что 
Что и требовалось доказать.
Задание 1.2. Найти область сходимости степенного ряда 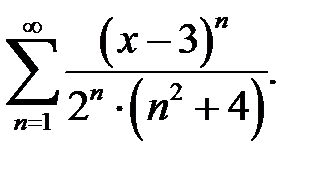
Теоретический минимум
_______________________________________________________________________________
Ряд, общим членом которого является функция, называется функциональным. Частным случаем функционального ряда является степенной ряд вида  Заменой
Заменой  ряд
ряд  можно свести к ряду
можно свести к ряду 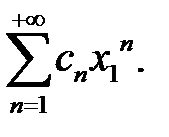
Теорема Абеля. Если степенной ряд  сходится при некотором значении
сходится при некотором значении 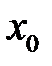 отличном от нуля, то он сходится на множестве
отличном от нуля, то он сходится на множестве 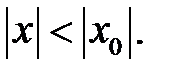
Существует такое число 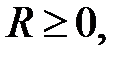 называемое радиусом сходимости ряда, что ряд
называемое радиусом сходимости ряда, что ряд  сходится при
сходится при 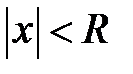 и расходится при
и расходится при 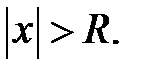
Радиус сходимости степенного ряда  можно найти по формулам:
можно найти по формулам:
 и
и 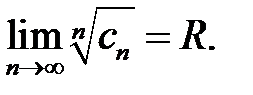
Интервал 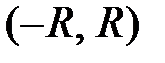 называют интервалом сходимости степенного ряда.
называют интервалом сходимости степенного ряда.
Замечание: интервал сходимости ряда 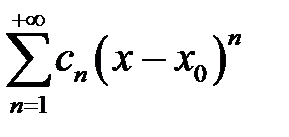 имеет вид
имеет вид 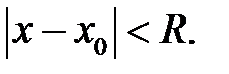
На границах интервала необходимо исследовать ряд на сходимость, подставив значения 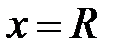 и
и 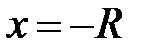 .
.
При подстановке вместо х конкретных значений степенной ряд  превращается в числовой (в общем случае ‑ знакопеременный), для которого можно определить: сходится он или нет.
превращается в числовой (в общем случае ‑ знакопеременный), для которого можно определить: сходится он или нет.
Члены знакопеременного ряда могут быть как положительными, так и отрицательными. Ряд вида 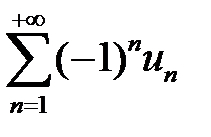 называется знакочередующимся.
называется знакочередующимся.
Если для ряда 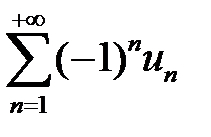 абсолютный ряд (ряд по модулю)
абсолютный ряд (ряд по модулю) 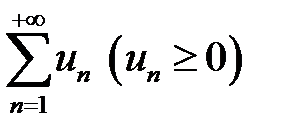 сходится, то говорят, что ряд
сходится, то говорят, что ряд 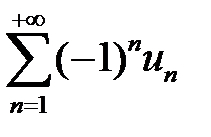 сходится абсолютно.
сходится абсолютно.
Признак Лейбница. Если для ряда 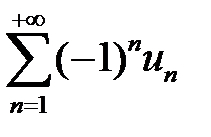 ряд
ряд 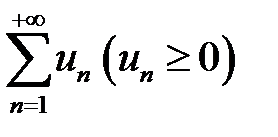 расходится, но выполняются условия:
расходится, но выполняются условия:
1)  ‑ бесконечно убывающая последовательность;
‑ бесконечно убывающая последовательность;
2) 
то ряд 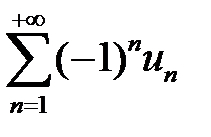 сходится условно.
сходится условно.
________________________________________________________________
Решение:
Найдем область сходимости данного степенного ряда. Для этого рассмотрим ряд по модулю 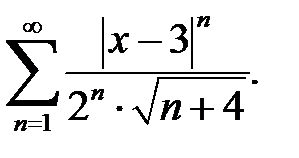
Найдем радиус сходимости ряда: 
Так как радиус сходимости ряда равен 2, то область сходимости ряда имеет вид 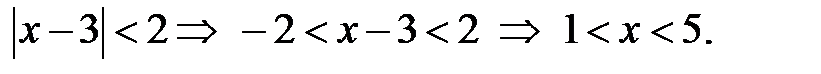
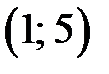 ‑ область сходимости степенного ряда,
‑ область сходимости степенного ряда, 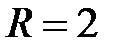 ‑ радиус сходимости.
‑ радиус сходимости.
Исследуем сходимость ряда на границах интервала сходимости. Сначала исследуем правую границу интервала.
При 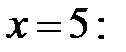
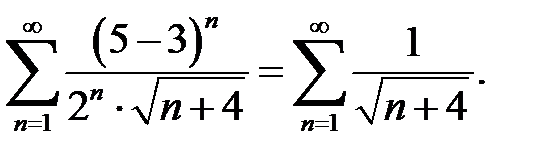
По предельному признаку сравнения для рядов 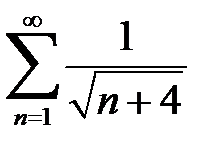 и
и 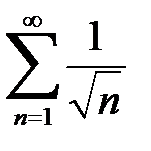 из условия
из условия 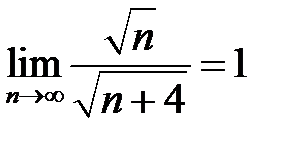 и расходимости ряда
и расходимости ряда 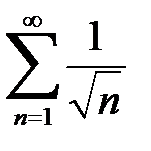 следует расходимость ряда
следует расходимость ряда 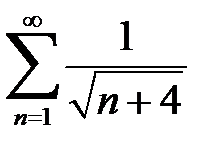 .
.
При 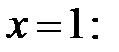

Ряд 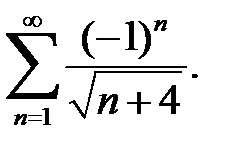 знакопеременный. Соответствующий ему ряд по модулю
знакопеременный. Соответствующий ему ряд по модулю 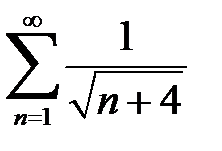 расходится, но по признаку Лейбница
расходится, но по признаку Лейбница 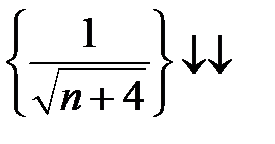 и
и 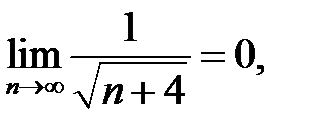 значит,
значит, 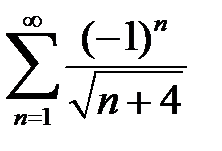 сходится условно.
сходится условно.
Таким образом, область сходимости степенного ряда ‑ 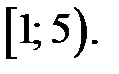 Радиус сходимости равен 2.
Радиус сходимости равен 2.
Ответ. Область сходимости данного степенного ряда ‑ 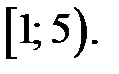
Замечание 1: если общий член степенного ряда представляет собой выражение в степени n или кратной n, то вместо признака Даламбера удобно применить радикальный признак Коши.
 ‑ условие сходимости ряда, позволяющее найти интервал и радиус сходимости степенного ряда
‑ условие сходимости ряда, позволяющее найти интервал и радиус сходимости степенного ряда 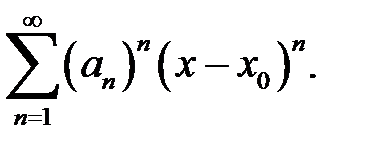
Замечание 2: Возможны случаи 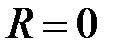 и
и 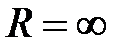 , например, для ряда
, например, для ряда  область сходимости состоит из точки
область сходимости состоит из точки 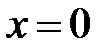 (
( 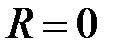 ); а для ряда
); а для ряда 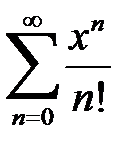 область сходимости
область сходимости  соответственно
соответственно 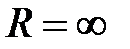 .
.
Задание 1.3.1. Вычислить 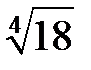 с погрешностью
с погрешностью 
Теоретический минимум
_____________________________________________________
Теорема о представлении функции степенным рядом: Пусть для 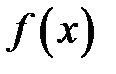 ,
, 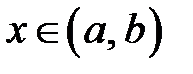 ,
, 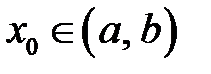 . Если
. Если
1) существуют все производные функции до n-го порядка включительно,
2) они ограничены на 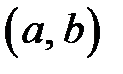 ,
,
тогда ряд Тейлора функции 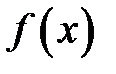 по степеням разности
по степеням разности 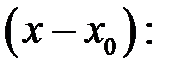
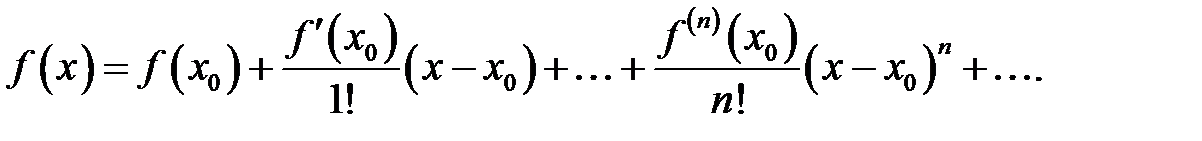
сходится к функции 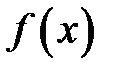 на
на 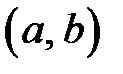 , т.е.
, т.е.

Рассмотрим разложения некоторых элементарных функций в степенные ряды:
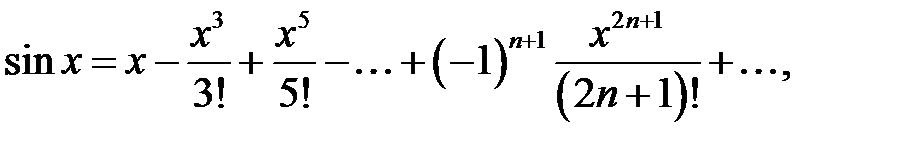
 .
.
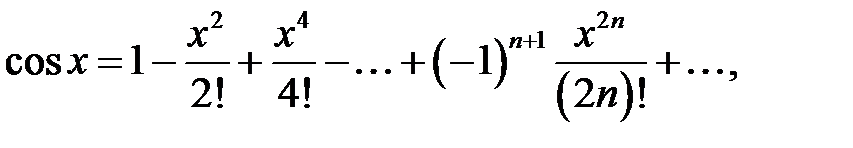
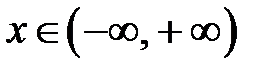 ,
,

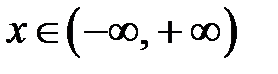 .
.
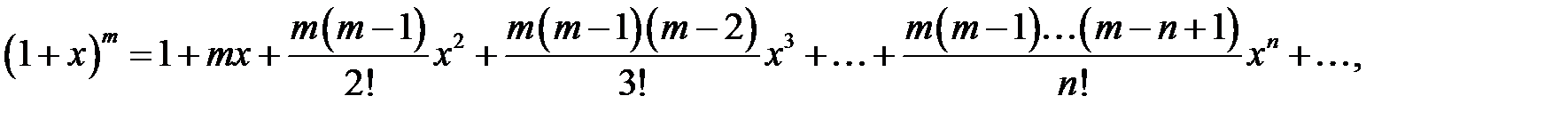 область сходимости биномиального ряда:
область сходимости биномиального ряда: 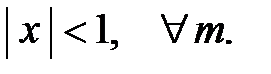
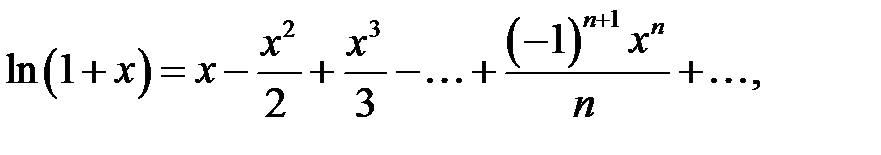
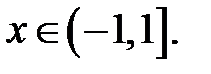
При приближенном вычислении суммы 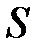 сходящихся рядов сумма ряда заменяется на его частичную сумму n слагаемых
сходящихся рядов сумма ряда заменяется на его частичную сумму n слагаемых  . Тогда возникает вопрос о погрешности вычисления – оценке суммы отбрасываемых слагаемых (это остаток ряда
. Тогда возникает вопрос о погрешности вычисления – оценке суммы отбрасываемых слагаемых (это остаток ряда 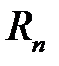 ).
).
Теорема об оценке остатка ряда. Ошибка при приближенном вычислении суммы сходящегося знакочередующегося ряда 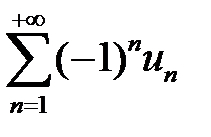 по модулю не превышает абсолютной величины первого отброшенного члена ряда:
по модулю не превышает абсолютной величины первого отброшенного члена ряда: 
Таким образом, чтобы вычислить приближенно сумму знакочередующегося ряда с заданной погрешностью, нужно:
1) найти первый член ряда по модулю не превышающий заданную погрешность;
2) отбросить при вычислении суммы ряда все его члены, начиная с найденного.
__________________________________________________
Решение:
Возьмем разложение в степенной ряд функции 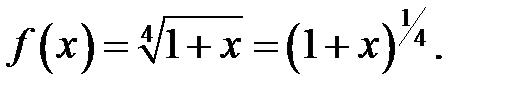
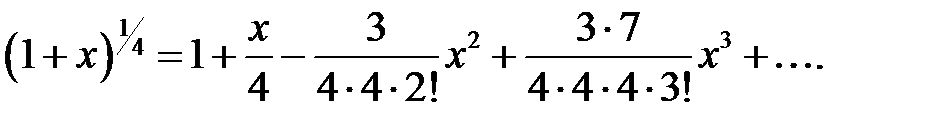
Преобразуем числовое выражение 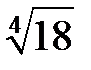 к виду, позволяющему использовать биномиальный ряд:
к виду, позволяющему использовать биномиальный ряд:
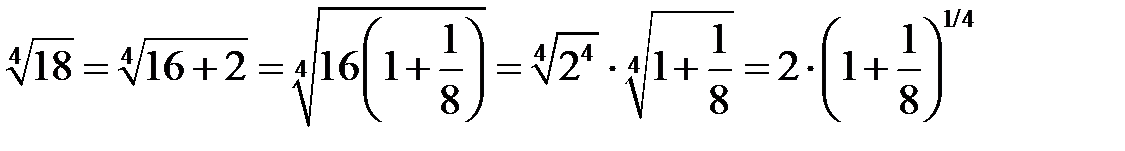 .
.
При  ,
, 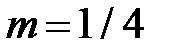 имеем
имеем 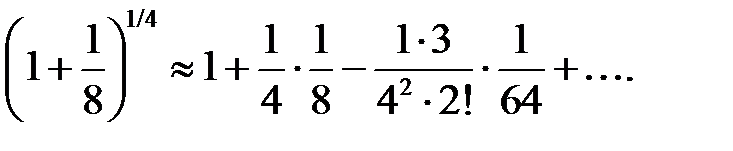
Получили знакочередующийся ряд, третье слагаемое которого 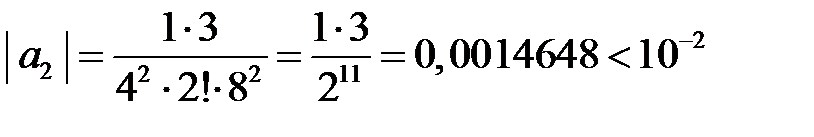 не превышает погрешности
не превышает погрешности 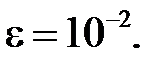 Таким образом, начиная с этого слагаемого, остаток ряда также не превышает заданной погрешности и его можно отбросить.
Таким образом, начиная с этого слагаемого, остаток ряда также не превышает заданной погрешности и его можно отбросить.
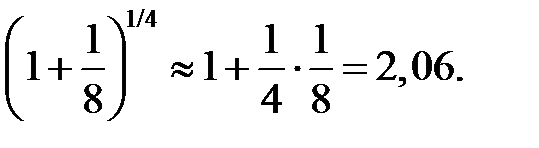
Ответ. 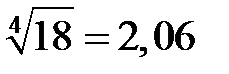 с погрешностью
с погрешностью 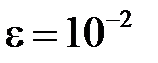 .
.
Задание 1.3.2. Вычислить приближенно значение интеграла 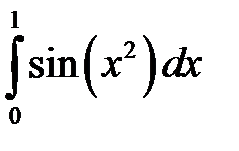 с погрешностью
с погрешностью 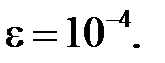
Решение. Имеем 
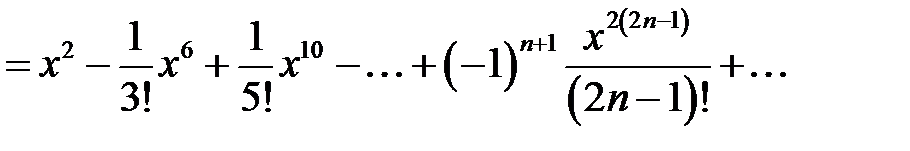 .
.
После интегрирования получаем

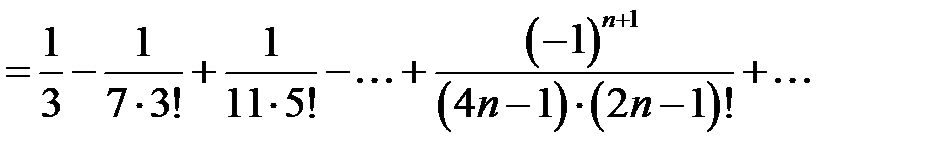 .
.
Поскольку ряд знакочередующийся, то 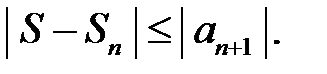 Потребуем
Потребуем 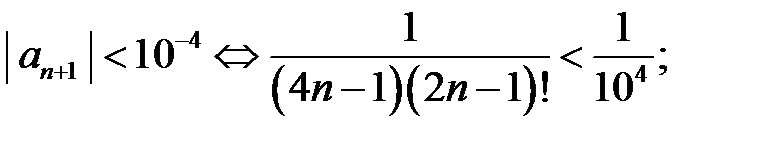 подберем
подберем 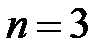 , удовлетворяющее неравенству
, удовлетворяющее неравенству 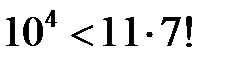 . Итак,
. Итак, 
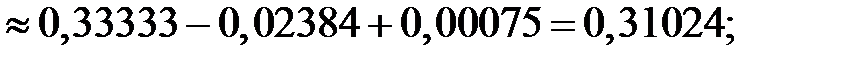 отсюда
отсюда 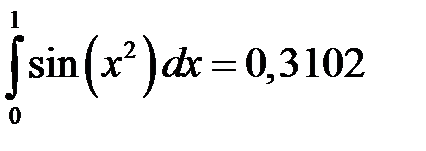 с
с 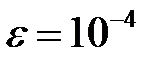 .
.
Дата добавления: 2019-09-13; просмотров: 180; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
