В каком случае функция называется
ПОНЯТИЕ ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
Теоретические сведения
Приступая к изучению функций нескольких переменных будем подробно останавливаться на функциях двух или трех переменных. Определения и выводы для функций большего числа переменных будут даваться по аналогии.
Что называется функцией двух переменных ?
Обозначим через D некоторое множество пар чисел
(х, у). На плоскости оно изобразится множеством точек с координатами х, у.
Определение. Если каждой паре чисел (х, у) из множества D по некоторому закону сопоставлено значение переменной z, то z называется функцией двух независимых переменных х, у. При этом множество D значений х и у при которых определяется функция z, называется областью определения этой функции.
Функцию двух переменных обозначают так:
z = f (x,y) (1.1)
Что называется функцией трех и более
Переменных ?
Определение функции двух переменных легко обобщить на случай трех и более переменных.
Определение. Если каждой рассматриваемой совокупности значений переменной x, y, z, …, , v, t соответствует определенное значение переменной u, то u называется функцией независимых переменных x, y, z, …, , v, t и обозначается:
u = f (x, y, z, …, , v, t).
Так же как и для функции двух переменных, можно говорить об области определения функции трех, четырех и более переменных. Так, например, для функции трех переменных областью определения является некоторая совокупность троек чисел (x, y, z). Поскольку каждая упорядоченная тройка чисел задает точку в пространстве, то область определения функции трех переменных можно представить как совокупность точек пространства.
|
|
|
Аналогично можно говорить об области определения функции четырех и более числа переменных как о совокупности упорядоченных четверок чисел (x, y, z, t) и любого числа упорядоченных чисел (x, y, z, … , v, t). Однако область определения функции четырех и большего числа переменных уже не допускает простого геометрического истолкования.
Что является графиком функции двух
Переменных ?
В уравнении (1.1.1) каждой точке М на плоскости с координатами (x, y) ставится в соответствие определенное значение переменной z. Тройка чисел (x, y, z = f (x, y)) определяет в пространстве единственную точку Р (x, y, z = f (x, y)). Очевидно (см. рис. 1), что проекцией точки Р на плоскость ХОУ является точка М (x, y).
 |
у
|
Рис. 1
Определение. Совокупность всех точек
Р (x, y, z = f (x, y)) называется графиком функции z = f (x, y).
В простейших случаях графиком функции z = f (x, y) является поверхность, проекция которой на плоскость ХОУ есть область D определения функции.
|
|
|
Уравнение (1.1.) может быть представлено в виде:
F (x, y, z) = 0. Если это уравнение является уравнением первой степени, то оно представляет собой некоторую плоскость. Поверхность, которую представляет уравнение второй степени называется поверхностью второго порядка. В разделе п.6 приведены канонические уравнения и построены изображения некоторых из них.
Что называется пределом функции двух
Переменных ?
Определение. Функция f (x, y) имеет предел в точке
М0 (x0, y0) равный числу А, если она определена в некоторой окрестности точки М0 (x0, y0), за исключением, быть может, самой этой точки и если существует предел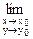 
f (x, y) = A, каким бы ни было направление движения от точки М (x, y) к точке М0 (x0, y0).
В каком случае функция называется
Непрерывной в точке ?
Определение. Функция f (x, y) непрерывна в точке
М0 (x0, y0), если выполняются три условия:
1) f (x, y) определена в некоторой окрестности и в самой точке;
2) существует предел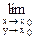 
f (x, y);
3) этот предел равен значению функции в точке
М0 (x0, y0).
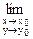f (x, y) = f (x0, y0).
Если хотя бы одно из этих условий не выполняется, то точка М0 является точкой разрыва функции.
|
|
|
Примеры решения задач
Задача 1. Выразить объем V цилиндра как функцию его высоты х и радиуса основания у.
Решение. Объем цилиндра равен V = p r2 H. В нашем случае Н = х, r = y. Получаем V = p y2 x.
Задача 2. Найти значение функции f (x, y) = xy +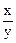 
при х = 1, у = -1 и при х = 
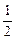, у = 3.
Решение. f (1; -1) = 1 × (-1) +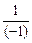 
= -1 – 1 = -2
f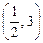 
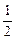= × 3 + 
= 
+ 
= 
= 
.
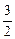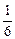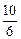Задача 3. Найти и изобразить область определения функций:
a) z = ln (x2 + y) б) z =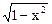 
+ 
.
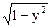Решение . а) Так как логарифмы определены только для положительных чисел, то должно удовлетворяться неравенство
х2 + у > 0 или у > -х2.
|
 |
б) Чтобы z имело действительное значение, нужно чтобы под каждым корнем было неотрицательное число, т.е. нужно рассмотреть систему неравенств:
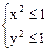Þ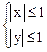 
Þ 
Þ 
Изобразим геометрически:
 |
Областью определения данной функции является совокупность точек плоскости, расположенная внутри квадрата, включая границы.
|
|
|
Задача 4. Построить график функции двух переменных:
а) z = x2, б)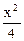 
+ 
- 
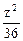= 1.
|
 |
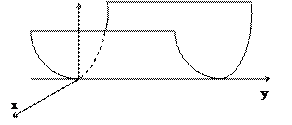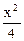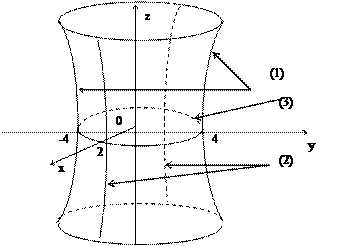
б) Поверхность: + - 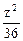= 1 задана каноническим уравнением однополостного гиперболоида с мнимой осью OZ (см. приложение 6.3).
Исследуем данную поверхность методом сечения координатными плоскостями. В сечении данной поверхности и плоскости х = 0 получим гиперболу
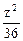- = 1. (1)
В сечении поверхности и плоскости у = 0 получим гиперболу
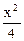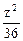- = 1. (2)
В сечении поверхности и плоскости z = 0 получим эллипс
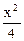+ = 1. (3)
Графиком данной функции является однополостной гиперболоид
Задача 5. Найти
.
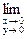
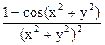Решение.
= 
= 
= 
=
= 
= 
= .
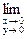
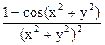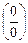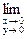
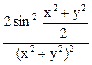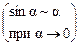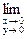
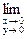
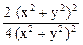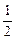Задача 6. Найти 
.
Решение. Предел не зависит от направления, по которому х и у стремятся к бесконечности. Пусть у = kx, тогда
= = 
= 
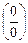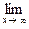
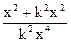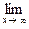
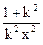= 0 при любом значении k.
Пример 7. Доказать, что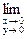 
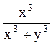не существует.
Решение. 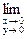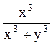= = 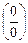(пусть у = kx) =
= 
= 
= 
.
Предел зависит от значения углового коэффициента k. Значит предел не существует.
Задача 8. Доказать, что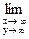 
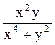не существует.
Решение.
= 
= 
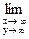
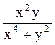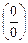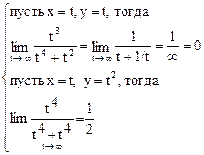
При разной скорости стремления х и у к бесконечности получаются разные ответы, а это значит, что предел не существует.
Задача 9. Указать геометрическое место точек разрыва функции
z =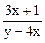 
.
Решение. Данная функция двух переменных z = 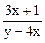не определена там, где знаменатель обращается в нуль,
у – 4х = 0 или у = 4х. Прямая у = 4х является линией разрыва данной функции.
Дата добавления: 2019-09-13; просмотров: 310; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!