Дифференциальные уравнения с разделяющими переменными
Уравнением с разделяющимися переменными называется уравнение, которое может быть записано в виде:
.
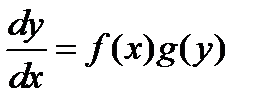Можно предложить следующую схему решения этого уравнения. Разделяем переменные, то есть уравнение переписываем в виде:
.
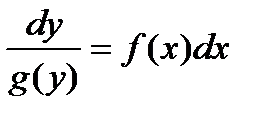Интегрируя левую и правую части этого уравнения, получаем:
,
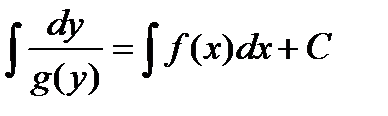где С – произвольная постоянная.
Полученное соотношение является общим интегралом исходного дифференциального уравнения.
Замечание. Если функция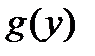 
равна нулю в точках 
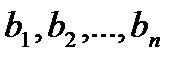, то функции 
, 
,…., 
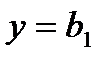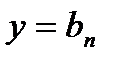являются решениями исходного уравнения. При изложенном методе такие решения могут быть потеряны, поэтому их рекомендуется выписать отдельно.
Пример. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде 
y(x,y)=C).
.
Для того, что бы убедиться, что данное уравнение действительно является уравнением с разделяющимися переменными, выразим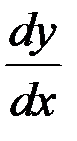 
. Имеем
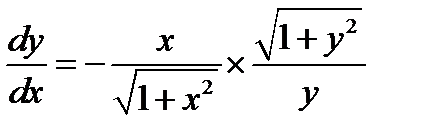
Тогда 
, 
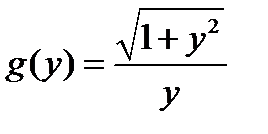. Заметим, что 
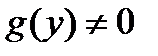. Разделяем переменные:
.
Интегрируя правую и левую части, получаем
.
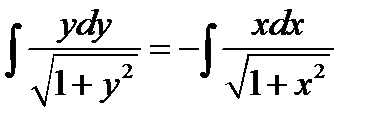Приведем схему вычисления интеграла: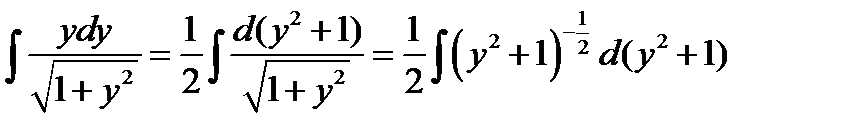 
= 
.
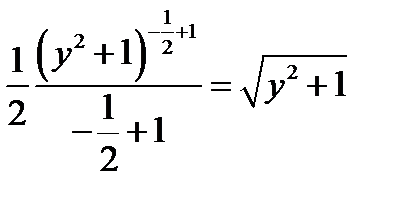После вычисления интегралов имеем: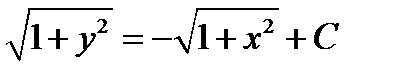 
.
Ответ: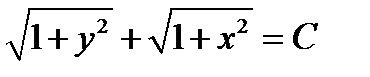 
.
Пример. Найти общий интеграл дифференциального уравнения.
.
|
|
|
Уравнение запишем в виде
.
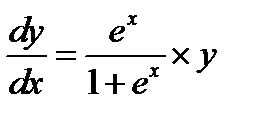Тогда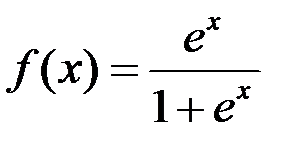 
, 
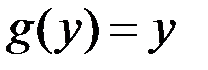. Заметим, что 
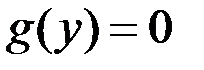при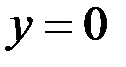 
. Следовательно, функция 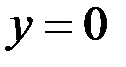является решением данного дифференциального уравнения.
В случае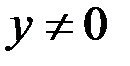 
разделяем переменные:
.
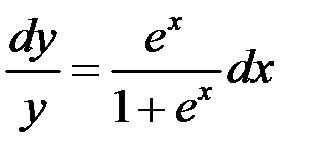Интегрируя правую и левую части, получаем
.
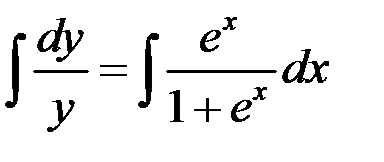Приведем схему вычисления интеграла
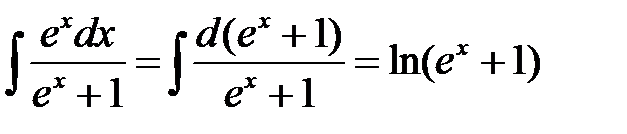
После вычисления интегралов имеем: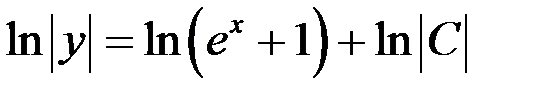 
, 
.
Потенцируя данное выражение, получаем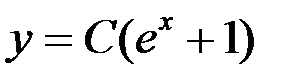 
. Отметим, что решение 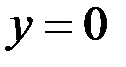содержится в полученном выражении общего решения при С=0.
Ответ: .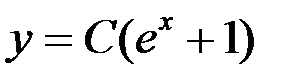
Пример. Найти общий интеграл дифференциального уравнения
.
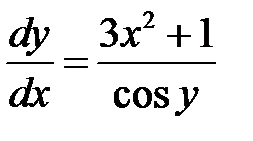Тогда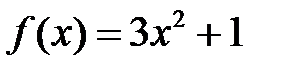 
, 
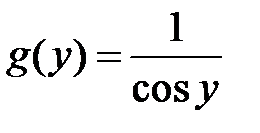. Заметим, что 
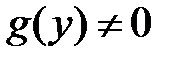. Разделяем переменные:
.
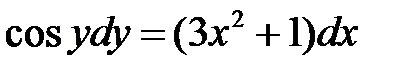Интегрируя правую и левую части, получаем
.
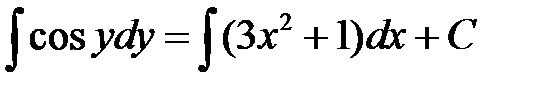После вычисления интегралов имеем: 
.
Ответ: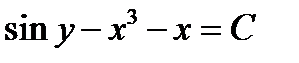 
.
Пример. Найти общий интеграл дифференциального уравнения
.
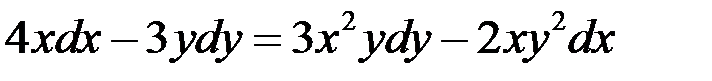Поясним, что такая запись подразумевает под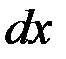 
дифференциал независимой переменной, под 
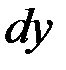- дифференциал неизвестной функции ( = 
).
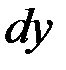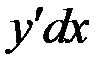Перенесем выражения, содержащие 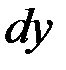в левую часть уравнения, выражения, содержащие - 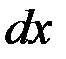в правую часть. После некоторых простых преобразований, получаем
|
|
|
.
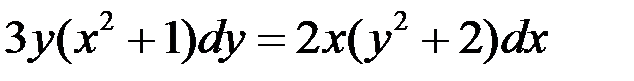Разделяем переменные
.
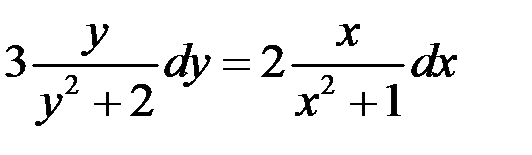Интегрируя правую и левую части, получаем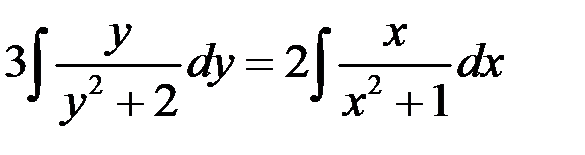 
.
Приведем схему нахождения интеграла
.
После вычисления интегралов имеем
.
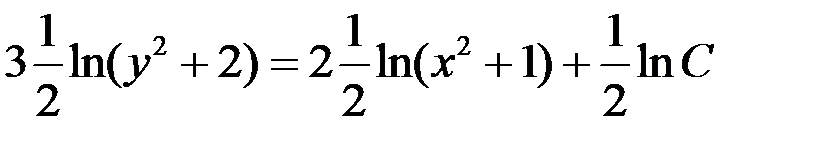Потенцируя полученное выражение, имеем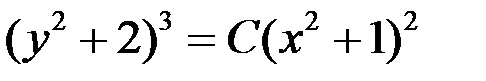 
.
Ответ: .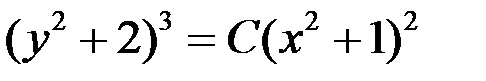
Задания для самостоятельной работы
Расчетная работа 3
1. Закончите определения:
1) Дифференциальным уравнением называется соотношение, в которое входят независимая переменная, неизвестная функция и … .
2) Наивысший порядок входящих в дифференциальное уравнение производных или дифференциалов искомой функции называется его … .
3) Дифференциальное уравнение называется уравнением первого порядка, если в него входят … . Уравнение первого порядка всегда можно представить в виде F (…)=0.
2. Подставляя функцию y = 2 sin x и ее производную в дифференциальное уравнение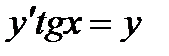 
, докажите, что она служит решением этого уравнения.
Доказательство.
1) Найдем производную функции y = 2 sin x: … .
2) Подставив эту функцию и ее производную в левую и правую части данного уравнения: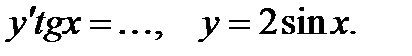 
|
|
|
3) Получим тождество: … .
3. Закончите определения:
1) Функция f ( x ) называется решением дифференциального уравнения первого порядка, если … .
2) Общим решением дифференциального уравнения первого порядка называется … .
3) Дифференциальное уравнение вида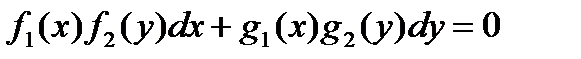 
называется … .
4. Докажите, что при любом значении C функция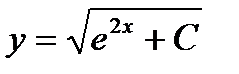 
служит решением уравнения 
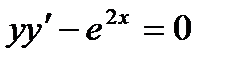. Подберите число Стак, чтобы решение удовлетворяло начальному условию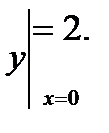 
5. Какие из нижеприведенных уравнений являются уравнениями: 1) первого порядка; 2) второго порядка:
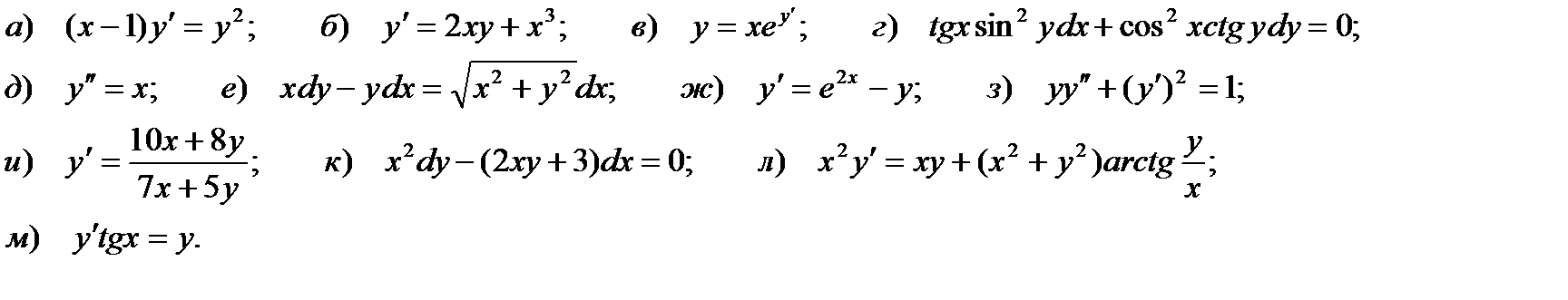
6. Проинтегрируйте уравнение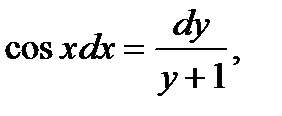 
в котором переменные разделены.
7. Решите уравнение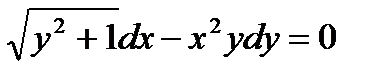 
с разделяющимися переменными. Найдите частное решение, удовлетворяющее начальному условию 
.
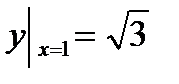Дата добавления: 2019-09-13; просмотров: 187; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!