Экстремум функции многих переменных
Точка 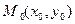 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  , если существует такая окрестность этой точки, что для всех точек
, если существует такая окрестность этой точки, что для всех точек 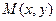 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство  (
(  ).
).
Экстремум функции носит локальный характер, поскольку речь идет о малой окрестности точки 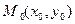 .
.
Теорема (необходимое условие экстремума функции многих переменных). Пусть точка  есть точку экстремума функции
есть точку экстремума функции 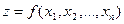 . Тогда частные производные этой функции по всем переменным в этой точке равны нулю. Иначе: в точке минимума или максимума функции многих переменных ее градиент равен нулю.
. Тогда частные производные этой функции по всем переменным в этой точке равны нулю. Иначе: в точке минимума или максимума функции многих переменных ее градиент равен нулю.
Точки, в которых выполняется необходимое условие экстремума, называются критическими или стационарными.
Теорема (достаточное условие экстремума функции двух переменных). Пусть 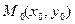 - стационарная точка функции
- стационарная точка функции  , в которой существуют ее непрерывные частные производные второго порядка. Обозначим
, в которой существуют ее непрерывные частные производные второго порядка. Обозначим 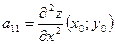 ,
,  ,
, 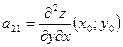 ,
, 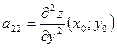 . Тогда:
. Тогда:
а) если 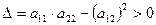 , то в точке
, то в точке 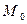 имеет место экстремум, причем при
имеет место экстремум, причем при 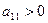 минимум, а при
минимум, а при 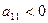 максимум;
максимум;
б) если 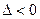 , то в точке
, то в точке 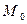 экстремума нет;
экстремума нет;
в) если 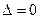 , то случай сомнительный и требуется дополнительное исследование (по определению).
, то случай сомнительный и требуется дополнительное исследование (по определению).
Условный экстремум. Метод множителей Лагранжа
Предположим, что экстремум функции многих переменных 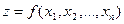 ищется не на всей области определения, а на множестве, удовлетворяющем некоторым ограничениям
ищется не на всей области определения, а на множестве, удовлетворяющем некоторым ограничениям 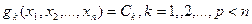 , которые называют условиями или уравнениями связи. В частности, для функции двух переменных
, которые называют условиями или уравнениями связи. В частности, для функции двух переменных  уравнение связи
уравнение связи  .
.
|
|
|
Точка 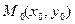 называется точкой условного максимума (минимума) функции
называется точкой условного максимума (минимума) функции  при ограничении
при ограничении  , если существует такая окрестность этой точки, что для всех точек
, если существует такая окрестность этой точки, что для всех точек 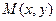 из этой окрестности, удовлетворяющих условию
из этой окрестности, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство  (
(  ).
).
Если уравнение связи  удается разрешить относительно одной из переменных, т.е. представить его в виде
удается разрешить относительно одной из переменных, т.е. представить его в виде 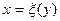 или
или  , то задача нахождения условного экстремума сводится к задаче нахождения экстремума функции одной переменной вида
, то задача нахождения условного экстремума сводится к задаче нахождения экстремума функции одной переменной вида 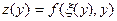 или
или 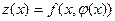 .
.
Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа. Для его реализации составляется функция Лагранжа вида 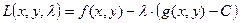 . Постоянная
. Постоянная 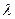 называется множителем Лагранжа.
называется множителем Лагранжа.
Теорема. Если точка 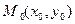 является точкой условного экстремума функции
является точкой условного экстремума функции  при ограничении
при ограничении  ,то существует значение
,то существует значение 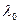 такое, что точка
такое, что точка 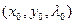 является точкой экстремума функции Лагранжа
является точкой экстремума функции Лагранжа  .
.
Тогда для нахождения условного экстремума функции  при ограничении
при ограничении  достаточно решить систему вида
достаточно решить систему вида
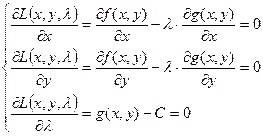 .
.
Пример. Исследовать на условный экстремум функцию 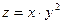 при ограничении
при ограничении 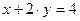 .
.
1. Сведем задачу к исследованию на безусловный экстремум функции одной переменной.
Для этого выразим из ограничения y:  и подставим в выражение для функции:
и подставим в выражение для функции:
|
|
|
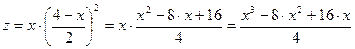 .
.
Необходимое условие экстремума функции одной переменной – равенство ее производной нулю. Тогда 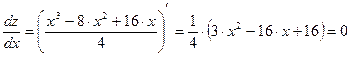 . Решая квадратное уравнение получим два корня
. Решая квадратное уравнение получим два корня 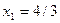 и
и 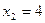 , т.е. две критические точки, в которых возможен экстремум.
, т.е. две критические точки, в которых возможен экстремум.
 Достаточное условие максимума предполагает, что знак первой производной функции меняет знак с “+” на “–“, а минимума – наоборот, с “–“ на “+“. Для рассматриваемой функции одной переменной можно предположить, что в точке
Достаточное условие максимума предполагает, что знак первой производной функции меняет знак с “+” на “–“, а минимума – наоборот, с “–“ на “+“. Для рассматриваемой функции одной переменной можно предположить, что в точке 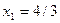 имеет место локальный максимум, а в точке
имеет место локальный максимум, а в точке 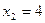 – локальный минимум. Из ограничения вычислим
– локальный минимум. Из ограничения вычислим  ,
, 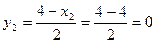 и предположим, что в точке
и предположим, что в точке 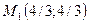 имеет место условный максимум функции
имеет место условный максимум функции 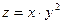 при ограничении
при ограничении 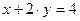 , а в точке
, а в точке 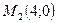 - ее локальный минимум.
- ее локальный минимум.
2. Выполним исследование функции на условный экстремум с помощью метода множителей Лагранжа. Для этого составим функцию Лагранжа 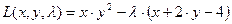 . Необходимое условие экстремума функции трех переменных – равенство нулю ее частных производных по всем переменным, т.е.
. Необходимое условие экстремума функции трех переменных – равенство нулю ее частных производных по всем переменным, т.е.
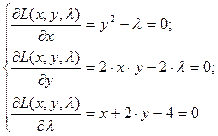 Из первых двух уравнений
Из первых двух уравнений 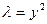 и
и 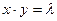 получаем
получаем  , откуда
, откуда  или
или 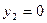 . Подстановка в первое и третье уравнения системы дает
. Подстановка в первое и третье уравнения системы дает 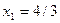 ,
, 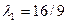 ,
, 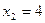 ,
, 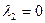 . Как и в первом случае получаем пару точек
. Как и в первом случае получаем пару точек 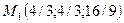 ,
, 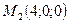 , являющихся критическими точками для функции Лагранжа.
, являющихся критическими точками для функции Лагранжа.
Проверим выполнение достаточных условий экстремума функции Лагранжа. Для этого введем понятие матрицы вторых производных функции многих переменных 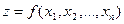 – матрицы Гессе. Она имеет вид
– матрицы Гессе. Она имеет вид
|
|
|
 .
.
Назовем 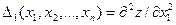 ,
, 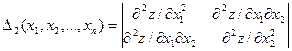 , …,
, …, 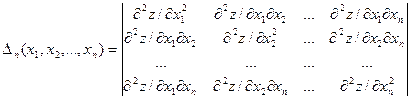 угловыми минорами матрицы Гессе. Тогда достаточное условие экстремума функции многих переменных определяет
угловыми минорами матрицы Гессе. Тогда достаточное условие экстремума функции многих переменных определяет
Теорема (критерий Сильвестра)
а) Для того чтобы стационарная точка 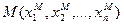 являлась точкой локального минимума функции
являлась точкой локального минимума функции 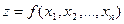 необходимо и достаточно, чтобы все угловые миноры ее матрицы Гессе, вычисленные в этой точке, были положительны, т.е.
необходимо и достаточно, чтобы все угловые миноры ее матрицы Гессе, вычисленные в этой точке, были положительны, т.е. 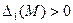 ,
, 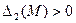 , …,
, …, 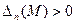 .
.
б) Для того чтобы стационарная точка 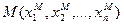 являлась точкой локального максимума функции
являлась точкой локального максимума функции 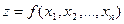 необходимо и достаточно, чтобы знаки угловых миноров ее матрицы Гессе, вычисленных в этой точке, чередовались, начиная с отрицательного, т.е.
необходимо и достаточно, чтобы знаки угловых миноров ее матрицы Гессе, вычисленных в этой точке, чередовались, начиная с отрицательного, т.е.  ,
, 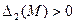 ,
,  , …
, …
Применим критерий Сильвестра для выяснения наличия и характера экстремума функции Лагранжа в рассматриваемой задаче. Для этого вычислим вторые производные функции Лагранжа по всем переменным:  ;
; 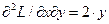 ;
; 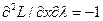 ;
; 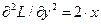 ;
; 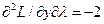 ;
; 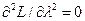 . Тогда матрица Гессе имеет вид
. Тогда матрица Гессе имеет вид
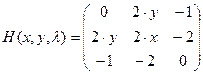 . Поскольку в нашем случае для обеих стационарных точек
. Поскольку в нашем случае для обеих стационарных точек 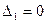 , то имеем сомнительный случай, требующий дополнительного исследования.
, то имеем сомнительный случай, требующий дополнительного исследования.
а) Точка 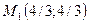
| x | y | z | ||
| 1,333133333 | 1,333433333 | 2,37037033 | ||
| 1,333233333
| 1,333383333 | 2,37037036 | ||
| 1,333333333 | 1,333333333 | 2,37037037 | ||
| 1,333433333 | 1,333283333 | 2,37037036 | ||
| 1,333533333 | 1,333233333 | 2,37037033 |
Расчеты, проведенные в окрестностях точки  показали, что функция
показали, что функция 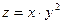 при ограничении
при ограничении 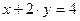 принимает значения, меньшие, чем значение функции в критической точке. Это позволяет утверджать, что в рассматриваемой точке имеет место локальный условный максимум функции
принимает значения, меньшие, чем значение функции в критической точке. Это позволяет утверджать, что в рассматриваемой точке имеет место локальный условный максимум функции 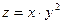 при ограничении
при ограничении 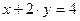 .
.
б) Точка 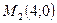
| x | y | z |
| 3,99980000 | 0,00010000 | 0,00000004 |
| 3,99990000 | 0,00005000 | 0,00000001 |
| 4,00000000 | 0,00000000 | 0,00000000 |
| 4,00010000 | -0,00005000 | 0,00000001 |
| 4,00020000 | -0,00010000 | 0,00000004 |
Расчеты, проведенные в окрестностях точки  показали, что функция
показали, что функция 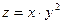 при ограничении
при ограничении 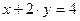 принимает значения, большие, чем значение функции в критической точке. Это позволяет утверджать, что в рассматриваемой точке имеет место локальный условный минимум функции
принимает значения, большие, чем значение функции в критической точке. Это позволяет утверджать, что в рассматриваемой точке имеет место локальный условный минимум функции 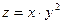 при ограничении
при ограничении 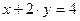 .
.
Ответ. функция 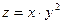 при ограничении
при ограничении 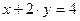 достигает локального условного максимума в точке
достигает локального условного максимума в точке 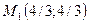 и локального условного минимума в точке
и локального условного минимума в точке 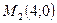 .
.
Двойные интегралы
В отличие от случая функции одной переменной, в случае двух и более переменных понятие первообразной и неопределенного интеграла ввести не удается.
Понятие определенного интеграла вводится на основании двумерного аналога интегральной суммы. Рассмотрим множество D на плоскости Oxy (рисунок 2) и построим покрывающее это множество решетку. Занумеруем клетки решетки двойными индексами 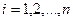 по горизонтали слева направо,
по горизонтали слева направо, 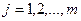 по вертикали снизу вверх. Обозначим
по вертикали снизу вверх. Обозначим  и
и  размеры клетки
размеры клетки  .
.
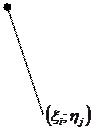 
| По мере уменьшения |
| Рисунок 2. Область интегрирования D |
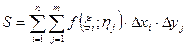 . Функция
. Функция 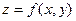 называется интегрируемой на множестве D, если существует конечный предел ее интегральной суммы на этом множестве при стремлении
называется интегрируемой на множестве D, если существует конечный предел ее интегральной суммы на этом множестве при стремлении 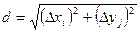 к нулю. Такой предел называют двойным интегралом функции
к нулю. Такой предел называют двойным интегралом функции 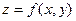 на множестве D. Таким образом,
на множестве D. Таким образом,
 .
.
Величина I не должна зависеть ни от способа разбиения D на ячейки, ни от выбора в каждой из них точки 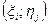 . С геометрической точки зрения
. С геометрической точки зрения 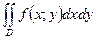 равен объему прямого цилиндрического тела с основанием D и ограниченного сверху поверхностью
равен объему прямого цилиндрического тела с основанием D и ограниченного сверху поверхностью 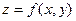 .
.
Множество D плоскости Oxy называют элементарным относительно оси Ox, если его граница может быть представлена в виде графиков двух непрерывных на отрезке [a;b] функций 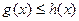 и отрезков прямых
и отрезков прямых  и
и 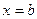 . Тогда двойной интеграл от функции
. Тогда двойной интеграл от функции 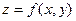 на множестве D может быть представлен в виде повторного интеграла как
на множестве D может быть представлен в виде повторного интеграла как
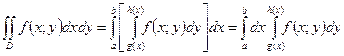 .
.
Дата добавления: 2019-09-13; просмотров: 365; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

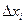 и
и  S(D), где S(Dклет) – площадь подмножества множества D, покрытого целыми клетками
S(D), где S(Dклет) – площадь подмножества множества D, покрытого целыми клетками 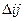 , S(D) – площадь множества D. В каждой клетке
, S(D) – площадь множества D. В каждой клетке