Производная по направлению. Градиент
Функции многих переменных
Пусть имеется n переменных величин 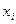 , i=1,2, …, n, и каждому набору их значений
, i=1,2, …, n, и каждому набору их значений 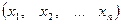 из некоторого множества X соответствует одно конкретное значение переменной величины z. Тогда говорят, что задана функция n переменных
из некоторого множества X соответствует одно конкретное значение переменной величины z. Тогда говорят, что задана функция n переменных 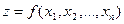 . Переменные
. Переменные 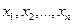 называют независимыми переменными или аргументами, z – зависимой переменной или функцией, а f определяет закон соответствия. Множество X называется областью определения функции и является подмножеством n-мерного пространства.
называют независимыми переменными или аргументами, z – зависимой переменной или функцией, а f определяет закон соответствия. Множество X называется областью определения функции и является подмножеством n-мерного пространства.
Замечание. Всякая функция многих переменных становится функцией меньшего числа переменных, если часть переменных зафиксировать.
Наиболее распространенным является задание функции многих переменных аналитически, т.е. явным уравнением 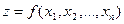 или неявным уравнением
или неявным уравнением  .
.
Частным случаем функции многих переменных является функция двух переменных, заданная явно в виде  или неявно –
или неявно – 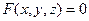 . Альтернативная форма задания – графически.
. Альтернативная форма задания – графически.
Графиком функции двух переменных 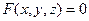 называется множество точек трехмерного пространства
называется множество точек трехмерного пространства 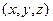 , обращающих уравнение
, обращающих уравнение 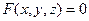 в верное равенство. Он представляет собой поверхность в пространстве
в верное равенство. Он представляет собой поверхность в пространстве 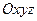 .
.
Замечание. Формально график можно задать и для функции n переменных 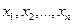 . В этом случае он называется гиперповерхностью в (n+1)-мерном пространстве.
. В этом случае он называется гиперповерхностью в (n+1)-мерном пространстве.
Линией уровня (изокривой) функции  называется множество точек плоскости
называется множество точек плоскости 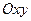 , для которых данная функция имеет одно и то же значение, т.е.
, для которых данная функция имеет одно и то же значение, т.е. 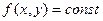 .
.
|
|
|
Окрестностью точки 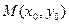 на плоскости называется круг, содержащий эту точку.
на плоскости называется круг, содержащий эту точку.
Число A называют пределом функции  в точке
в точке 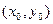 (или при
(или при 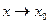 и
и 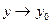 ), если для любого сколь угодно малого числа
), если для любого сколь угодно малого числа  найдется положительное число
найдется положительное число 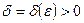 такое, что для всех точек
такое, что для всех точек 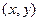 , отстоящих от
, отстоящих от 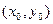 на расстояние
на расстояние 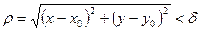 , выполняется неравенство
, выполняется неравенство  .
.
Предел обозначают как 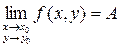 .
.
На плоскости существует бесконечно много направлений, по которым точка может стремиться к 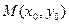 . Если зафиксировать одну из переменных и совершить предельный переход по второй, то получится два предела вида
. Если зафиксировать одну из переменных и совершить предельный переход по второй, то получится два предела вида 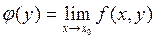 и
и 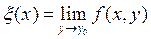 . Совершая предельный переход по второй переменной получим
. Совершая предельный переход по второй переменной получим  и
и 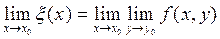 , которые называют повторными пределами функции двух переменных. В общем случае они могут не совпадать друг с другом или с пределом функции в точке
, которые называют повторными пределами функции двух переменных. В общем случае они могут не совпадать друг с другом или с пределом функции в точке 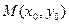 . Их равенство определяется теоремой.
. Их равенство определяется теоремой.
Теорема. Если существуют 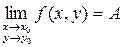 ,
, 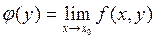 для всех y из некоторой окрестности y0 и
для всех y из некоторой окрестности y0 и 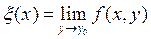 для всех x из некоторой окрестности x0, то существуют оба повторных предела функции
для всех x из некоторой окрестности x0, то существуют оба повторных предела функции  в точке
в точке 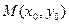 , которые совпадают с A.
, которые совпадают с A.
В общем случае пределы функции многих переменных по разным направлениям могут быть различными.
Функция  называется непрерывной в точке
называется непрерывной в точке 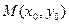 , если она определена в этой точке .имеет в ней конечный предел, и значение предела совпадает со значением функции в точке .т.е.
, если она определена в этой точке .имеет в ней конечный предел, и значение предела совпадает со значением функции в точке .т.е. 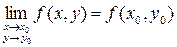 . С геометрической точки зрения это означает, что график данной функции в данной точке представляет собой сплошную нерасслаивающуюся поверхность.
. С геометрической точки зрения это означает, что график данной функции в данной точке представляет собой сплошную нерасслаивающуюся поверхность.
|
|
|
Функция  называется непрерывной на множестве M, если она непрерывна в каждой точке этого множества.
называется непрерывной на множестве M, если она непрерывна в каждой точке этого множества.
Полным приращением функции  в точке
в точке 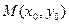 называют величину
называют величину  . Частными приращениями по соответствующим переменным будут
. Частными приращениями по соответствующим переменным будут 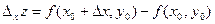 и
и 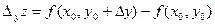 . При этом полное приращение не равно сумме частных, т.е.
. При этом полное приращение не равно сумме частных, т.е.  .
.
Частной производной функции многих переменных по одной из этих переменных называют предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю, если этот предел существует.
В случае функции двух переменных 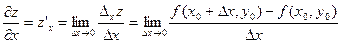 и
и 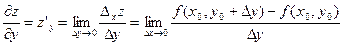 . Каждая из частных производных функции двух переменных сама является функцией двух переменных.
. Каждая из частных производных функции двух переменных сама является функцией двух переменных.
Частные производные старших порядков определяются последовательно через производные меньших порядков. Так, производные второго порядка функции  определяются следующим образом:
определяются следующим образом: 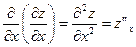 и
и 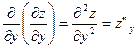 - частные производные второго порядка по x и y соответственно. Помимо частных производных второго порядка существуют смешанные производные второго порядка
- частные производные второго порядка по x и y соответственно. Помимо частных производных второго порядка существуют смешанные производные второго порядка 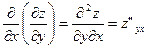 и
и 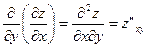 . Смешанные производные второго порядка не всегда совпадают.
. Смешанные производные второго порядка не всегда совпадают.
|
|
|
Теорема (достаточное условие равенства смешанных производных второго порядка функции двух переменных). Пусть в некоторой окрестности точки 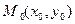 существуют частные производные функции
существуют частные производные функции 
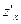 ,
, 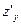 ,
, 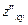 и
и  , причем
, причем 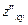 и
и  непрерывны в точке
непрерывны в точке 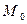 . Тогда
. Тогда  .
.
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 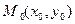 , если ее полное приращение в этой точке допускает представление в виде
, если ее полное приращение в этой точке допускает представление в виде  , где
, где 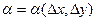 и
и 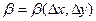 - бесконечно малые величины при
- бесконечно малые величины при  .
.
Дифференциалом функции двух переменных  называют линейную относительно
называют линейную относительно 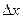 и
и 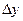 часть ее полного приращения, т.е.
часть ее полного приращения, т.е. 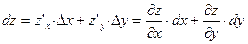 .
.
Теорема (достаточное условие дифференцируемости функции многих переменных). Если в некоторой окрестности точки 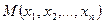 существуют частные производные первого порядка функции
существуют частные производные первого порядка функции 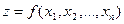 по всем переменным, которые являются непрерывными в точке M, то функция z дифференцируема в этой точке.
по всем переменным, которые являются непрерывными в точке M, то функция z дифференцируема в этой точке.
Производная по направлению. Градиент
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 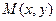 , l – некоторое направление, заданное единичным вектором
, l – некоторое направление, заданное единичным вектором 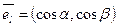 , где
, где  и
и 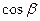 – направляющие косинусы, т.е. косинусы углов, образованных вектором
– направляющие косинусы, т.е. косинусы углов, образованных вектором 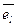 с осями координат.
с осями координат.
При перемещении в направлении l из точки 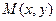 в точку
в точку 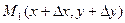 функция
функция  получает приращение
получает приращение 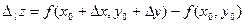 , называемое приращением функции z в данном направлении l.
, называемое приращением функции z в данном направлении l.
|
|
|
Производной 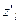 по направлению l функции
по направлению l функции  называется предел отношения приращения функции в этом направлении
называется предел отношения приращения функции в этом направлении 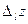 к величине перемещения
к величине перемещения 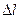 при стремлении последнего к нулю, т.е.
при стремлении последнего к нулю, т.е. 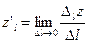 . Она характеризует скорость изменения функции в направлении l.
. Она характеризует скорость изменения функции в направлении l.
Для вычисления производной по направлению используется формула
 .
.
Градиентом функции  называется вектор, координатами которого являются частные производные функции, т.е.
называется вектор, координатами которого являются частные производные функции, т.е. 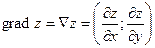 .
.
Градиент функции z в точке M0 показывает направление максимальной скорости изменения этой функции в этой точке. Кроме того, вектор градиента в точке (если он отличен от нулевого вектора) перпендикулярен линии уровня функции z, проходящей через эту точку.
Дата добавления: 2019-09-13; просмотров: 97; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
