Ряды Фурье. Ортогональная система функций. Тригонометрический ряд Фурье
Рядом Фурье для периодической с периодом T=2π функции y=f(x), определённой на интервале [-π;π], называется тригонометрический ряд:
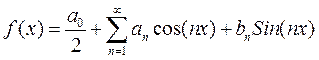
Коэффициенты 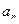 ,
, 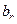 ,
, 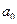 находятся по формулам Фурье:
находятся по формулам Фурье:
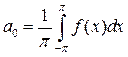
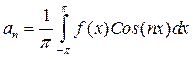
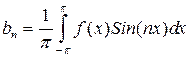

Нахождение коэффициентов для триг - го ряда Фурье (теорему док).
Теорема: Если функция  определена и непрерывна на
определена и непрерывна на 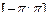 и разлагается в тригонометрический ряд
и разлагается в тригонометрический ряд 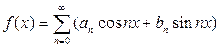 (*), который можно почленно интегрировать, то это разложение единственное.
(*), который можно почленно интегрировать, то это разложение единственное.
Доказательство:
Умножим обе части (*) на 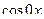 , проинтегрируем на
, проинтегрируем на 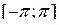
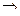
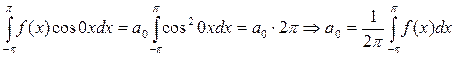 . Аналогично умножим (*) на
. Аналогично умножим (*) на 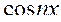 и проинтегрируем.
и проинтегрируем. 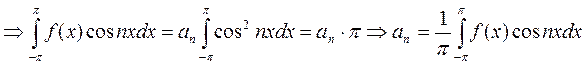 .
.
Умножим (*) на 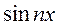 и проинтегрируем на
и проинтегрируем на 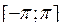
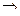
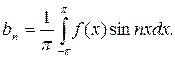 Коэффициенты равенства (*) определяются единственным образом
Коэффициенты равенства (*) определяются единственным образом 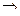 такое разложение единственное
такое разложение единственное 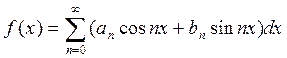 ,
, 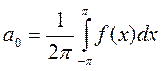 ,
, 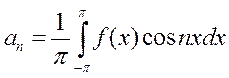 ,
, 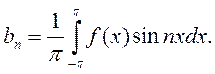 Ч.т.д.
Ч.т.д.
Теорема Дирихле(без док.)
Пусть ограниченная функция 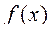 удовлетворяет на
удовлетворяет на  условиям:
условиям:
1) интервал  можно разбить на конечное число интервалов, в которых функция – непрерывная и монотонная.
можно разбить на конечное число интервалов, в которых функция – непрерывная и монотонная.
2) если xo т. разрыва функции 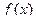 , то
, то  пределы
пределы  ,
, 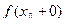 . Т.е точка x0 – т.разрыва 1 рода.
. Т.е точка x0 – т.разрыва 1 рода.
Тогда ряд Фурье функции 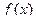 сходится и имеет место равенство
сходится и имеет место равенство 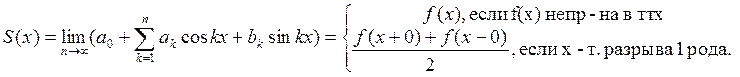
Замечание. Если представить функцию,  периодически продолженную на всю ось Ox c периодом
периодически продолженную на всю ось Ox c периодом 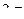 , то утверждение теоремы будет справедливо
, то утверждение теоремы будет справедливо 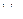 .
.
Тригонометрический ряд Фурье на произвольном интервале (- l , l ).
Пусть f(x) периодическая с периодом  ,
, 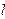 ≠
≠  .. Разложим функцию в ряд Фурье. Для этого сделаем замену
.. Разложим функцию в ряд Фурье. Для этого сделаем замену 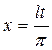 . Тогда f(
. Тогда f( 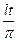 ) – периодическая функция от переменной t с периодом 2
) – периодическая функция от переменной t с периодом 2  , её можно разложить на x
, её можно разложить на x 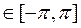 .
.
|
|
|
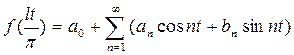 , где
, где 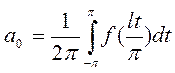 ,
, 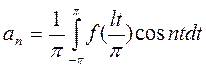 ,
, 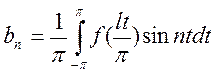 ,
, 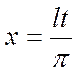
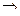
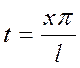 ,
, 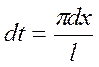 , тогда
, тогда
 ,
, 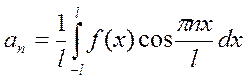 ,
, 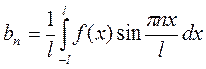
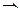
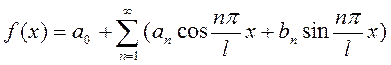 .
.
Дата добавления: 2019-09-13; просмотров: 191; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
