Теорема об интегрировании методом подстановки (доказать)
Пусть f(x) – непрерывная на [a,b], ф-ия x=φ(t) – непрерывно дифференцируема на [t1,t2], причем φ: [t1,t2] → [a,b] и φ(t1)=a φ(t2)=b тогда

Док-во: Пусть F(x) первообразная для f(x) на [a,b], тогда по формуле Ньютона-Лейбница
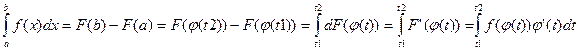
Приложения определенного интеграла: вычисление площади плоской фигуры (вывод формулы в полярной системе), длины дуги (вывод формулы в ДСК), объема тела вращения относительно Ox (вывод формулы)
 Площадь в полярной:
Площадь в полярной:
За базовую фигуру в полярной системе принимается криволинейный сектор, ограниченный ρ=ρ(φ), φ=α φ=β. Предполагаем, что ρ=ρ(φ) – непрерывна на [α,β]. Для вычисления площади примем алгоритм составления интегральной суммы к последующим предельным переходом к определенному интегралу.
1. Разобьем отрезок [α,β] на n элементарных отрезков α= φ0< φ1< φ2<… < φn= β
Δ φk = φk-1- φk
2. На каждом из отрезков [φk-1- φk] k=1,n выбираем произвольную точку Θk и найдем ρk=ρ(Θk) k=1,n
Каждый криволинейный сектор заменим на круговой сектор с радиусом ρk
3. Площадь кругового сектора Sk= 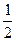 ρ2(Θk)Δ φk
ρ2(Θk)Δ φk
S= 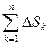 =
= 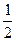 ρ2(Θk)Δ φk
ρ2(Θk)Δ φk
4. За точное значение SOAB примем интегральную сумму при λ= 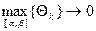
S= 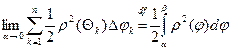
 Длина дуги в ДСК:
Длина дуги в ДСК:
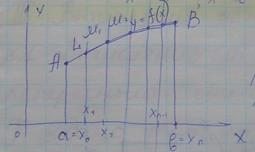
Пусть ф-ия y=f(x) определена и непрерывна на [a,b] и кривая L – график этой ф-ии. Требуется найти длину плоской кривой L, заключенной между вертикальными кривыми x = a, x = b
1. Рассмотрим произвольное разбиение [a,b] точками x0=a, x1, x2,…, xn=b на n частей. Через точку xk, k=1,n проведем вертикальные линии параллельные Oy до пересечения с кривой L. Дуга AB разбивается на n частей. Соединим соседние точки отрезками и получим ломанную, вписанную в дугу AB.
|
|
|
2. ln = 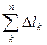 l ≈ ln - ломаная
l ≈ ln - ломаная
3. Mk-1Mk – длина стягивающей хорды. Т.к. Mk-1 (xk-1; f(xk-1)), Mk (xk; f(xk))
Δl = | Mk-1 + Mk| = 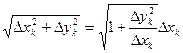 по теореме Лагранжа
по теореме Лагранжа
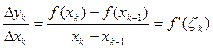 ξk
ξk  [xk-1, xk]
[xk-1, xk] 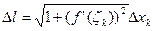
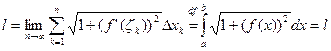
Вычисление объема тела вращения: Рассмотрим тело, образованное вращением вокруг оси Ox криволинейной трапеции aABb ограниченной кривой y=f(x), осью Ox и x = a, y = b
1. Рассмотрим произвольное разбиение [a,b] x0 = a < x1< x2<… < xn = b
обозначим Δxk = xk-xk-1 
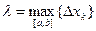
2. Пересекаем тело вращения плоскостями перпендикулярными Ox и получи круги, радиусы которых равны |yk|=|f(xk)| На каждом [xk-1- xk] выберем произвольным образом ξk S(ξk)= πf2(ξk) (S=πR2)
3. Предположим на любом частном отрезке ф-ия S=S(x) совпадает с S(ξk). Тогда объем частичного цилиндра: ΔVk = S(ξk)Δxk = πf2(ξk)Δxk 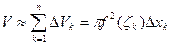
4. 
Понятие несобственного интеграла I рода.
Несобственным интегралом с бесконечным верхним пределом интегрирования (I рода) от непрерывной ф-ии y=f(x) на промежутке [a, ∞) называется предел интеграла.
I(b)= 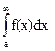 =
= 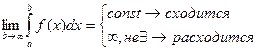
10. Признаки сходимости. Первый признак сравнения(теорему доказать). Второй (предельный) признак сравнения(без док.)
|
|
|
Признаки сходимости:
Если функция f(x)>=0 на [a, +∞),то для сходимости несобственного интеграла 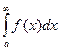 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 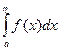 , a<=η<+∞ было ограниченно т.о. существует A>0 |
, a<=η<+∞ было ограниченно т.о. существует A>0 |  η
η  [a, +∞)
[a, +∞) 
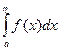 <=A
<=A
Первый признак сравнения:
Теорема1:
Путь заданы две функции f(x) и g(x), неотрицательные на [a,+∞) и 0<=f(x)<=g(x)  x
x 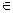 [a,+∞).
[a,+∞).
Тогда 1) если 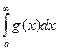 –сходится, то
–сходится, то 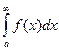 тоже сходится.
тоже сходится.
2)если 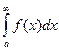 - расходится, то
- расходится, то 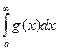 - расходится.
- расходится.
Доказательство:
1) 

 [a,+∞) т.к. 0<=f(x)<=g(x) имеем интеграл
[a,+∞) т.к. 0<=f(x)<=g(x) имеем интеграл  <=
<= 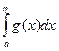 ,
,
Если 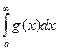 - сходится, то по Лемме
- сходится, то по Лемме 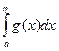 -ограничена.
-ограничена. 
 -ограниченные по Лемме.
-ограниченные по Лемме.
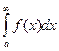 - сходится
- сходится
2) Если 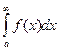 расходится, то по п.1) интеграл
расходится, то по п.1) интеграл 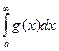 не может сходится
не может сходится 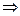
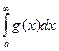 - расходится.
- расходится.
Теорема2:Предельный признак сравнения.
Пусть f(x) и g(x) неотрицательная на [a,+ 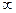 ), y(x)
), y(x) 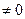
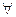 x
x  [a,+
[a,+  ) и пусть существует конечный предел отношения
) и пусть существует конечный предел отношения 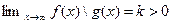 , в этом случае
, в этом случае 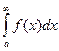 и
и 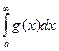 сходятся и расходятся одновременно. Ряд g(x) называется функцией сравнения.
сходятся и расходятся одновременно. Ряд g(x) называется функцией сравнения.
11. Понятие несобственного интеграла
Пусть f(x) определена на [a,b) и неограниченна в левосторонней окрестности точки (в точке разрыва 2 рода). Т.е.  .
.
Будем считать, что f(x) интегрируема на [a,b-  ],
], 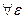 >0: I=I(
>0: I=I(  )=
)= 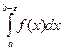 зависщий от переменного верхнего предела.
зависщий от переменного верхнего предела.
|
|
|
Df: Несобственный интеграл от функции f(x), непрерывный на промежутке [a,b) и имеющий разрыв 2 рода в т 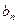
 или несобственный интеграл 2 рода называется предел интеграла I(
или несобственный интеграл 2 рода называется предел интеграла I(  ):
):
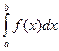


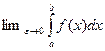 ,
, 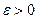
Аналогично звучит df если f(x) имеет ∞ в точке а.
12. Признаки сравнения (без док.)
Терема3:
Пусть в левой(правой) окрестности точки b (точки а) определены неотрицательные функции f(x) и g(x), причем 0<=f(x)<=g(x).
Тогда 1) из сходимости н.и. 2 рода 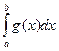
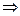
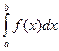 - сходится
- сходится
2)из расходимости н.и. 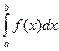
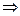 расходится
расходится 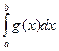
Теорема4:(Предельный признак сравнения)
Пусть f(x) и g(x) неотрицательные, и g(x)  0 на промежутке [a,b), а в точке b функция терпит
0 на промежутке [a,b), а в точке b функция терпит 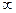 разрыв 2 рода, и если существует
разрыв 2 рода, и если существует  , то
, то
1) если 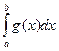 сходится, 0<=k<=+∞, то
сходится, 0<=k<=+∞, то 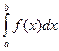 - сходится.
- сходится.
2) Если 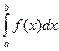 расходится, 0<=k<=+∞, то
расходится, 0<=k<=+∞, то 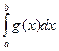 - расходится
- расходится
13. Теорема об абсолютной сходимости несобственного интеграла (доказать)
Теорема: Если несобственный интеграл абсолютно сходится, то он и сходится.
Доказательство:
Пусть несобственный интеграл  сходится.
сходится.
Рассмотрим 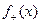 = {f(x), если f(x)>=0
= {f(x), если f(x)>=0
{0, если f(x)<0
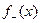 = {0, если f(x)>0
= {0, если f(x)>0
{f(x), если f(x)<=0
f(x)= 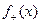 =
= 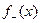
14. Основные топологические понятия: замкнутая и открытая область, расстояние между точками, связная и несвязная область и т.д.(×)
|
|
|
Определение: Множество всех упорядоченных наборов (x1,x2,…,xn) действительных чисел x1,x2,…,xn – называется n-мерным арифметическим точечным пространством и обозначается R. А его элементы называются точками пространства R.
Числа x1,x2,…,xn – называются координатами токи (x1,x2,…,xn). Обозначают прописными буквами латинского алфавита M(x1,x2,…,xn)
Расстоянием ρ(M’,M’’) между двумя точками M’(x1,x2,…,xn) и M’’(x1’,x2’,…,xn’) n- мерного пространства называется число:
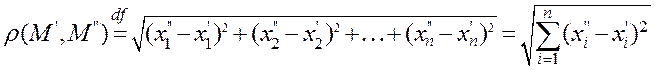
Геометрическое место точек P, координаты которого удовлетворяют z=f(x,y) называется графиком функции 2-х переменных.
1) ε - окрестность т. 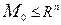 называется множество точек, отстоящих от точки M0 на расстояние меньше чем ε
называется множество точек, отстоящих от точки M0 на расстояние меньше чем ε 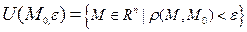
Проколотая окрестность. ε -окрестность т. M0.
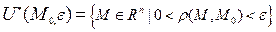
2)  Точка
Точка 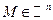 называется внутренней точкой множества
называется внутренней точкой множества 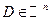 , если она принадлежит множеству D вместе с некоторой своей окрестностью.
, если она принадлежит множеству D вместе с некоторой своей окрестностью.
3)  Точка
Точка 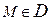 называется граничной точкой множества D, если в любой её окрестности найдутся точки принадлежащие D, и не принадлежащие D.
называется граничной точкой множества D, если в любой её окрестности найдутся точки принадлежащие D, и не принадлежащие D.
Совокупность всех граничных точек называется границей множества D.
4) 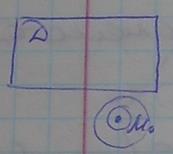 Точка
Точка  называется внешней точкой множества
называется внешней точкой множества 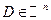 , если E существует окрестность т. M0 в которой нет точек множества D.
, если E существует окрестность т. M0 в которой нет точек множества D.
5) Множество D точек пространства  называется открытым, если все его точки – внутренние.
называется открытым, если все его точки – внутренние.
6) Точка  называется предельной точкой множества D, если существует последовательность т.
называется предельной точкой множества D, если существует последовательность т. 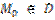 такая, что
такая, что 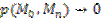 (Mn сходится к т. M0)
(Mn сходится к т. M0)
7) Множество D называется замкнутым, если оно содержит все граничные точки.
8) Множество D называется связным, если любые две точки M и B можно соединить ломаной, целиком лежащей в этом множестве.
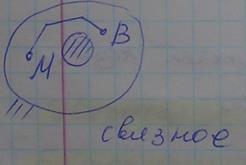

9) Открытое связное множество называется областью
10) Множество D – называется ограниченным, если все его точки содержатся в некотором n-мерном шаре, т. е. 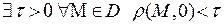
15) Понятие функции нескольких переменных. Область определения, область значений, график, линии (поверхности) уровня.(×)
ФНП: Пусть множество 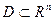 (произвольное подмножество
(произвольное подмножество  -мерного пространства). Если правило
-мерного пространства). Если правило  каждой точке
каждой точке  ставит в соответствие некоторое определенное действительное число
ставит в соответствие некоторое определенное действительное число  , то говорят, что на множестве
, то говорят, что на множестве 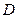 задана числовая функция или отображение
задана числовая функция или отображение  от
от  переменных:
переменных:
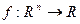 или
или 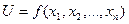 ; где
; где 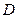 -область определения,
-область определения,  -аргументы, независимые переменные,
-аргументы, независимые переменные, 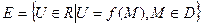 - множество значений.
- множество значений.
График функции: Графиком функции нескольких переменных называется множество 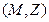 , где
, где  . Если
. Если 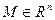 ,
,  , то
, то 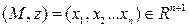
Область определения, область значений: Если каждой паре (x,y) из множества D по некоторому закону поставлено в соответствие значение переменной z из множества E, то переменную z будем называть функцией двух переменных и обозначать: z=f(x,y). Множество D называется областью определения, а множество E – областью значений функции.
Область определения: Совокупность пар (x,y) значений x и y, при которых определяется функция z=f(x,y) называется областью определения этой функции.
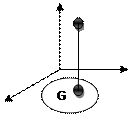 Пусть z=f(x,y) , D(f)=G – область
Пусть z=f(x,y) , D(f)=G – область 
P P(x,y,z)=P(x,y,f(x,y))
Поверхность (или линия) уровня: Поверхность (линия), в точках которой поле принимает постоянные значения, называется поверхностью (линией) уровня скалярного поля.
Семейство поверхностей (линий) уровня может быть задано уравнением U=C, C-const
Если  , n=2 – линия уровня
, n=2 – линия уровня
n=3 – поверхность уровня
16. Понятие предела ФНП. Свойства пределов ФНП
Понятие предела функции нескольких переменных аналогично понятию пре дела функции одной переменной.
Определение по Коши: Число A называется пределом функции U = f ( M ) в т. M 0 , если 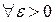 существует
существует 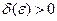 такое, что для точки M удовлетворяет условию:
такое, что для точки M удовлетворяет условию:
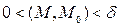 выполняется неравенство
выполняется неравенство 
Обозначается: 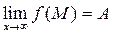
Краткая символическая запись:  Смысл данного определения состоит в том, что значение функции f ( x , y) как угодно мало отличается от A в точках достаточно малой окрестности точки M0 .В частности, для функции двух переменных f ( x , y )
Смысл данного определения состоит в том, что значение функции f ( x , y) как угодно мало отличается от A в точках достаточно малой окрестности точки M0 .В частности, для функции двух переменных f ( x , y )
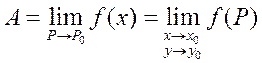
Свойства пределов ФНП
1) Если P0(x0,y0) не является бесконечно "удаленной точкой, то U ( P 0, δ )

2) Если P0(∞,∞ ) - бесконечно удаленная точка, то под окрестностью U ( P 0 , δ)
понимается мн-во точек, удовлетворяющих неравенству 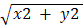 > δ Описать самостоятельно окрестность U ( P0,δ) точки P0 (x0,∞).
> δ Описать самостоятельно окрестность U ( P0,δ) точки P0 (x0,∞).
3) Предел функции нескольких переменных существует, если его значение не зависит от способа стремления точки P к точке P0. Поэтому, если значение предела хотя бы при одном способе стремления P к P 0 отличается от других, предел не существует.
4) Как и для функции одной переменной, для функции нескольких переменных вводится понятие бесконечно малых и бесконечно больших величин. Согласно определению, величина f ( P ) называется бесконечно малой (бесконечно большой) при стремлении P к P0, если

В последнем случае неравенство (1) в определении предела заменяется |f(P)| > ε
Пусть заданы две функции 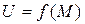 и
и 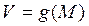 определены на
определены на  и пусть
и пусть 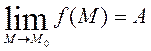 и
и  , тогда
, тогда
1) 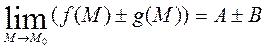
2) 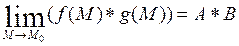
3)  , В≠0
, В≠0
17) Непрерывность ФНП
Пусть U=f(M) определена D и в предельной т. M0
Функции U=f(M) называется непрерывной в точке Mo, если выполняются условия:
1) U=f(M) определена в т.M0 и некоторой ее окрестности
2) 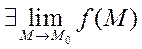
3) 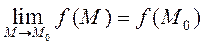
18) Свойства ФНП, непрерывной в точке (без док.) (×)
Функции нескольких переменных на замкнутых множествах обладают свойствами аналогичными свойствам функций одной переменной на отрезке.
Свойства непрерывных функций.
1. Сумма, разность и произведение двух непрерывных функций является непрерывной функцией.
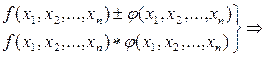 (сумма, разность, произведение непрерывных функций есть непрерывные функции)
(сумма, разность, произведение непрерывных функций есть непрерывные функции)
2. 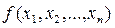 ,
, 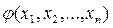 ,
, 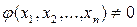
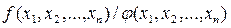 -(частное непрерывная функция есть непрерывная фу-я если
-(частное непрерывная функция есть непрерывная фу-я если 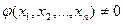 )
)
3. 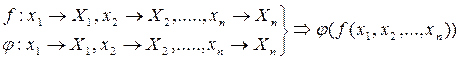 -непрерывная функция
-непрерывная функция
4. Основные функции нескольких переменных являются непрерывными всюду на своей области определения.
5. Все функции нескольких переменных являются непрерывными в своей области определения.
19. Теорема о непрерывности элементарных ФНП в области определения (без доказательства). Свойства ФНП, непрерывной на множестве (без док.) (×)
Теорема.
Если f(x1, x2, x3…) непрерывна в ограниченной замкнутой области G, то она в этой области:
1. Ограничена, т.е. 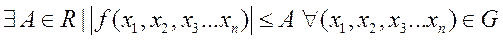
2. Принимает на G наибольшее и наименьшее значение, т.е. 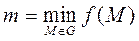
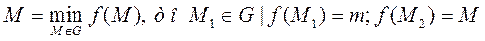
3. Принимает на G любое промежуточное значение между m и M, т.е. если

Определение элементарных функций нескольких переменных строятся как суперпозиция элементарных функций одной переменной с помощью конечного числа арифметических операций и композиции (возведение в степень).
Теорема о непрерывности элементарных функций.
Любая элементарная функция нескольких переменных непрерывна на области своего определения.
Свойства непрерывных функций на множестве.
1. Сумма, разность и произведение двух непрерывных функций на множестве является непрерывная функция.
2. Частное непрерывных функций на множестве есть непрерывная функция (если функция, стоящая в знаменателе не обращается в ноль на этом множестве).
3. Основные функции нескольких переменных являются непрерывными всюду на своей области определения.
4. Все элементарные функции нескольких переменных непрерывны в своей области определения.
Дата добавления: 2019-09-13; просмотров: 764; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
