Производные тригонометрических функций.

 

1) .

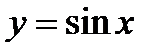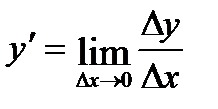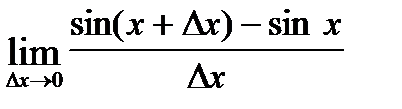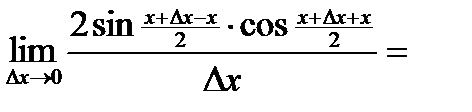
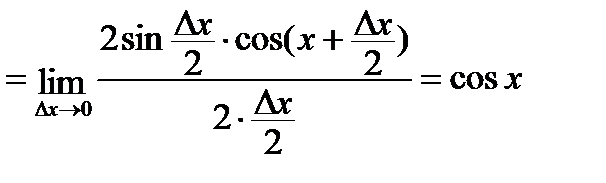= = . Þ .

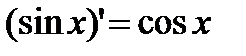2) .

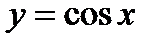Доказывается аналогично первому: .

3) .

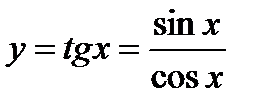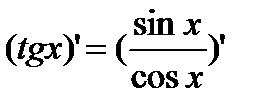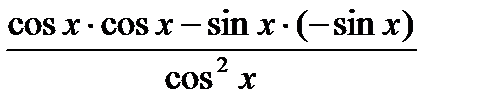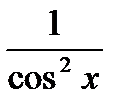 =  =  Þ .

4) y=ctg x. .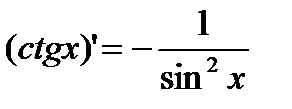

 

Производные обратных тригонометрических функций.

1) y=arcsin x. .

2) y=arccos x. .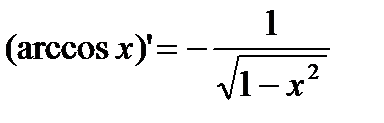

3) y=arctg x. .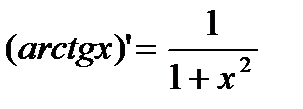

4) y=arcctg x. .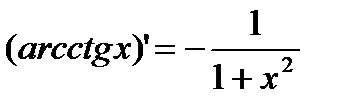

 

Производные логарифмической и показательной функций.

 

1. .

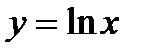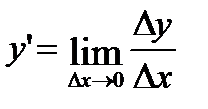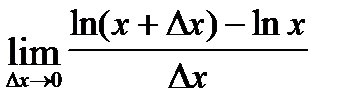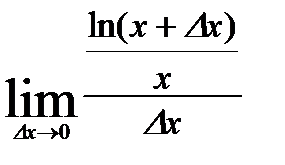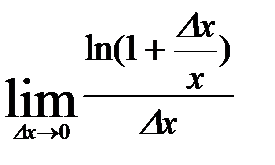 =  =  =  = следствие из второго замечательного предела =  =  

´= .

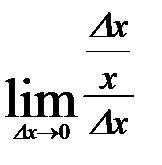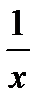
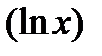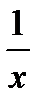2. 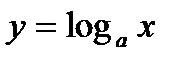.  y= .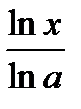

 =  = .

.

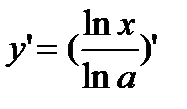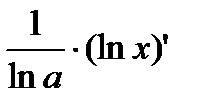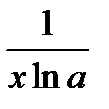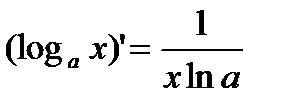3. .

 =  =  =  =

=  = .

.

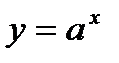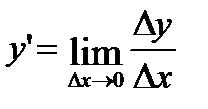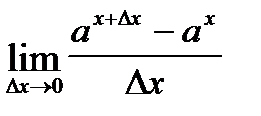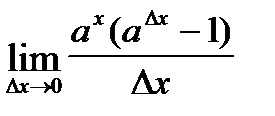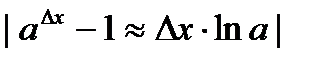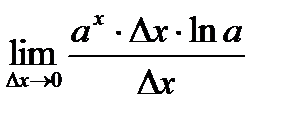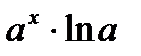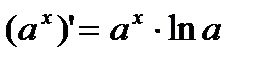4. y=е^x.

.

.

 

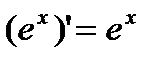Производная сложной функции.

Теорема. Пусть функция 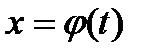 имеет производную в точке t₀, а функция  имеет производную в точке . Тогда производная сложной функции 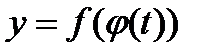 в точке t₀ будет равна:

.

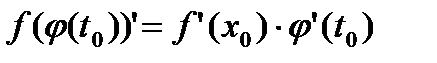Пример: ,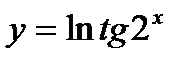

 

Производная обратной функции.

 

Теорема. Пусть функция  монотонна на интервале (a,b) (возрастает или убывает) и имеет производную в каждой точке этого интервала. Если в точке x₀ 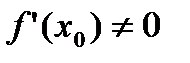, то обратная функция  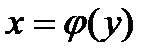также имеет производную в соответствующей точке y₀, причем

.

 

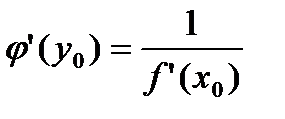Логарифмическое дифференцирование.

Производная степенной функции.

 

Пусть функция .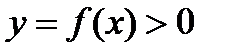

Прологарифмируем эту функцию по основанию e: .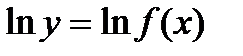

Возьмем производную левой и правой части равенства, считая y функцией от x: .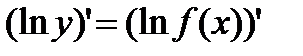

Þ производная правой части: .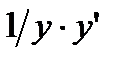

Выразим отсюда y¢.

Описанный прием называется логарифмическим дифференцированием.

.

; ; ; ;

 

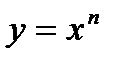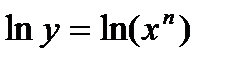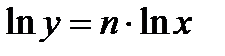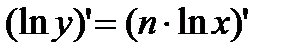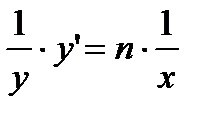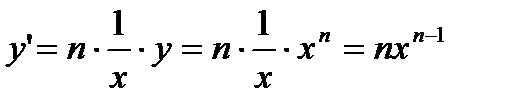
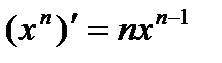
Производная неявной функции.

 

Уравнение F(x,y)=0 задает y, как неявную функцию от x.

Пример:  (  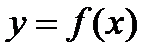– явное задание функции).

Чтобы продифференцировать функцию, заданную неявно, нужно взять производную левой и правой части уравнения, считая y функцией от x. Затем выразить из этого уравнения y¢.

Пример: ; ; 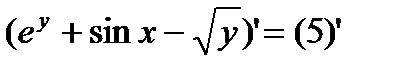; ; 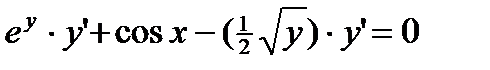 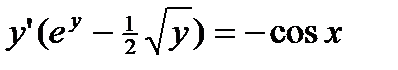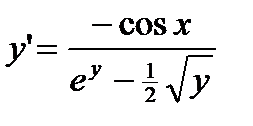– производная.

 

Производная функции, заданной параметрически.

 

Функция задана параметрически, если зависимость y от x осуществляется с помощью параметра t: 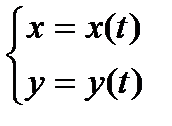, где tÎT.

Пример: 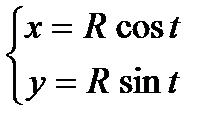 — параметрическое уравнение окружности с центром C(0,0) и радиусом R.

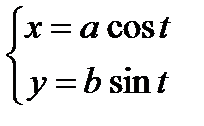              — параметрическое уравнение эллипса, где a и b большая и малая полуоси.

Вычисление производных функции, заданной параметрически:

Чтобы получить явную зависимость y от x, нужно из системы исключить параметр t. Для этого предполагаем, что для функции 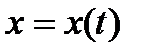 на промежутке t существует обратная функция 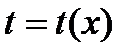. Тогда  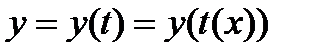– сложная функция. Продифференцируем: .

; .

 

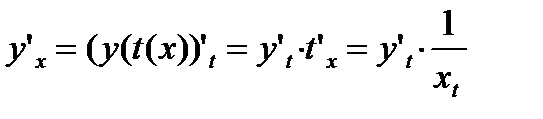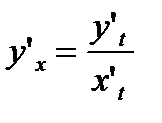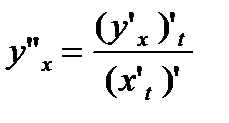Дифференциал, его геометрический смысл, правила вычисления.

 

Дифференциал функции.

Пусть функция 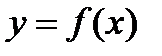 определена в точке x₀ и ее окрестности. Дадим x₀ приращение Dx, тогда функция получает приращение Dy: 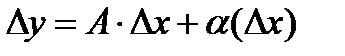, где А - число, a(Dx) - б/м более высокого порядка малости чем Dx. Выражение A×Dx называют главной частью приращения Dy.

Определение: Дифференциалом функции 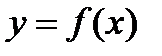 называют главную часть ее приращения, линейную относительность Dx.

Обозначают: dy или df, dy=df=A·Dx, где Dx ® 0.

Определение: Функция, имеющая дифференциал в точке x₀, называется дифференцируемой в этой точке.

Теорема: Для того чтобы функция 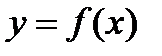 была дифференцируема в точке x₀ необходимо и достаточно, чтобы она имела в точке x₀ конечную производную.

Дифференциал 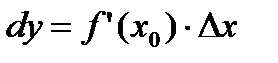, где Dx – приращение аргумента и обозначается dx, тогда окончательно дифференциал:

.

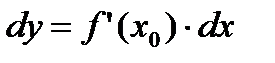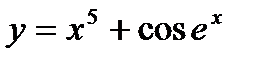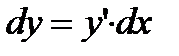Пример:  Þ  Þ .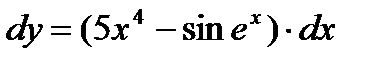

---

Дата добавления: 2019-09-13; просмотров: 245; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!