Признаки монотонности функции.
Пусть функция 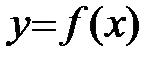 определена и непрерывна на промежутке (a;b).
определена и непрерывна на промежутке (a;b).
Определение: Функция 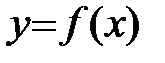 называется неубывающей (невозрастающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется
называется неубывающей (невозрастающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется 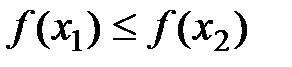 (
(  ).
).
Определение: Функция 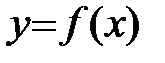 называется возрастающей (убывающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется
называется возрастающей (убывающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется 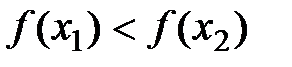 (
( 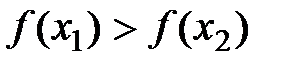 ).
).
Теорема 1.
Для того чтобы функция 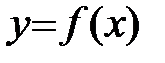 , дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е.
, дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е.  , и достаточно, чтобы
, и достаточно, чтобы  .
.
Доказательство:
Необходимость.
Пусть f(x) возрастает на (a;b). Тогда для любых 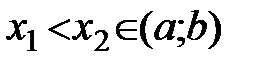 выполняется
выполняется 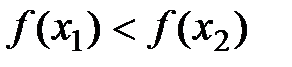 .
.
Þ 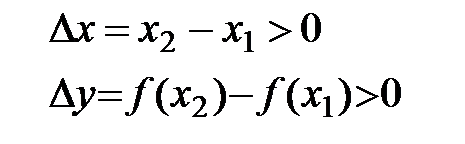 Þ
Þ 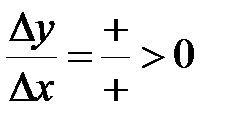 .
.
По определению производной: 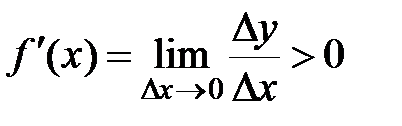 .
.
Достаточность.
Пусть  на (a;b). f(x) дифференцируема на (a;b). Выберем на этом промежутке 2 точки х1; х2.
на (a;b). f(x) дифференцируема на (a;b). Выберем на этом промежутке 2 точки х1; х2.
Тогда на (х1; х2) выполняется условие теоремы Лагранжа:
существует точка с Î(х1; х2) такая, что  .
.
Þ 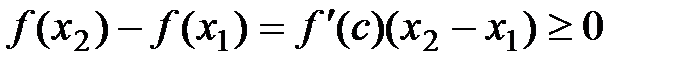 (т.к.
(т.к. 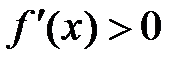 ).
).
Þ  . Þ
. Þ 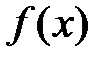 возрастает на (a;b).
возрастает на (a;b).
Ч.т.д.
Теорема 2.
Для того чтобы функция 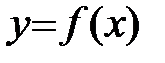 , дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке
, дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке  и достаточно, чтобы
и достаточно, чтобы 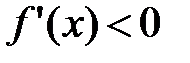 .
.
Доказательство проводится аналогично.
Пример: Найти интервалы возрастания и убывания функции 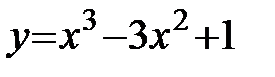 .
.
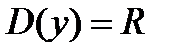 .
.

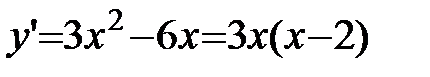 .
.
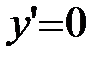 Þ
Þ 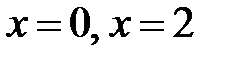 .
.
 Экстремум функции.
Экстремум функции.
Пусть функция 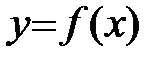 определена в окрестности точки x0.
определена в окрестности точки x0.
Определение: Точка x0 называется точкой строгого локального максимума, если существует такая ее окрестность точки, в которой выполняется неравенство 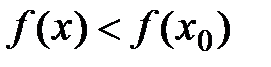 .
.
|
|
|
x0 — max.
Определение: Точка x0 называется точкой строгого локального минимума, если существует такая ее окрестность точки, в которой выполняется неравенство 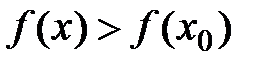 .
.
x0 — min.
Точки локального максимума и минимума называются точками экстремума.
Необходимое условие экстремума дифференцируемой функции.
Если функция  , дифференцируемая в точке x0, имеет в этой точке экстремум, то производная
, дифференцируемая в точке x0, имеет в этой точке экстремум, то производная 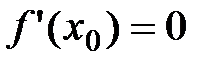 .
.
Доказательство:
Пусть для определенности точка x0 — max.
Тогда по определению существует такая ее окрестность  , в которой выполняется неравенство
, в которой выполняется неравенство 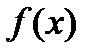 <
<  .
.
Т.о. на интервале  в точке x0 функция принимает наибольшее значение
в точке x0 функция принимает наибольшее значение 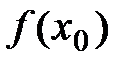 .
.
Тогда по теореме Ферма: 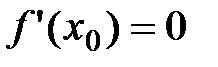 .
.
Аналогично доказывается для минимума функции.
Ч.т.д.
Однако, возможна ситуация, когда функция  будет иметь экстремум в точке x0 в том случае, когда производная
будет иметь экстремум в точке x0 в том случае, когда производная  не существует.
не существует.
Точки, в которых производная 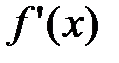 либо равна 0, либо не существует, называются критическими точками производной.
либо равна 0, либо не существует, называются критическими точками производной.
Замечание 1: Обратное утверждение не верно. Не всякая функция, производная которой в точке равна нулю или не существует, имеет в этой точке экстремум.
Замечание 2. Функция имеет экстремум только в критических точках.
Достаточное условие экстремума.
|
|
|
Пусть функция определена в критической точке x0 и дифференцируема в некоторой окрестности этой точки, за исключением, может быть, самой x0. Если «при переходе» через точку x0 слева направо производная меняет знак с плюса на минус, то x0 – точка максимума; с минуса на плюс – точка минимума.

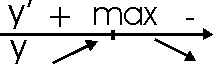
Доказательство:
Пусть производная меняет знак с «+» на «-».
Тогда слева от х0, т.е. на (х0-δ,х0) 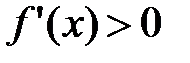 .
.
| y |
| x |
| 0 |
| x0 |
| f(x0) |
| x0+d |
| x0-d |
 возрастает.
возрастает.
Справа от х0, т.е. на (х0, х0+δ)  .
.
Þ справа от х0 функция  убывает.
убывает.
Т.о. в окрестности точки х0 выполняется
неравенство 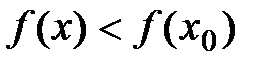 .
.
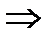 х0 – точка локального максимума.
х0 – точка локального максимума.
Аналогично доказывается для минимума.
Ч.т.д.
Пример: Исследовать функцию на монотонность и найти точки экстремума.
а) 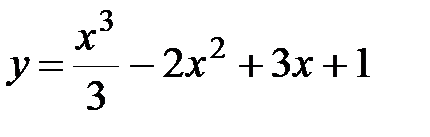 .
.
1. Область определения функции D(y)=R.
2. 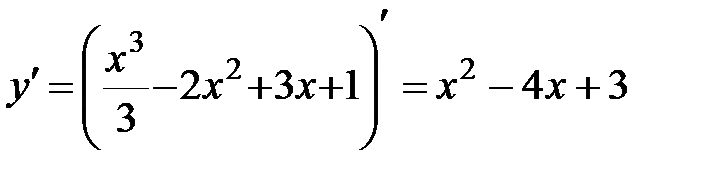 .
.
Критические точки:  .
.  Þ
Þ 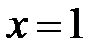 ,
, 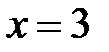 .
.
| x | (-∞;1) | x=1 | (1;3) | x=3 | (3;+∞) |
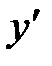
| + | 0 | – | 0 | + |
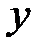
| возрастает | max

| убывает | min y(3)=1 | возрастает |
б)  .
.
1. Область определения функции D(y): x¹-1.
2. 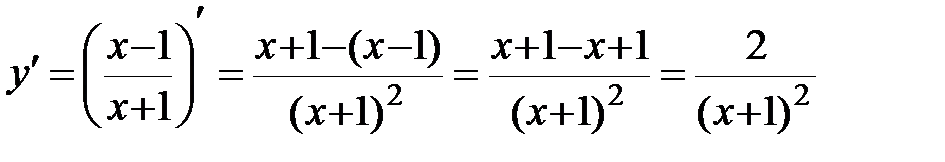 ;
;
 .
.
Критические точки:  , т.е. числитель равен нулю Þ нет точек;
, т.е. числитель равен нулю Þ нет точек;
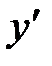 – не существует, т.е. знаменатель равен нулю Þ
– не существует, т.е. знаменатель равен нулю Þ 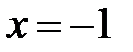 .
.
| x | (-∞;-1) | x=-1 | (-1;+∞) |
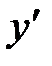
| + | не существует | + |

| возрастает | не существует | возрастает |
Точек экстремума нет.
|
|
|
Дата добавления: 2019-09-13; просмотров: 254; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
