Тригонометрические подстановки.
Интегралы 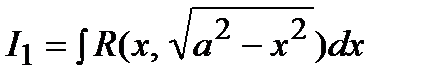 ,
, 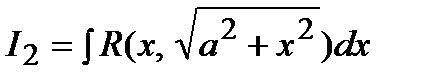 ,
, 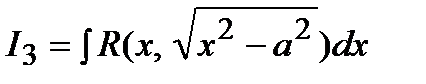 приводятся к интегралам от рациональных функций относительно
приводятся к интегралам от рациональных функций относительно 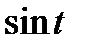 и
и 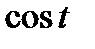 с помощью следующих тригонометрических подстановок:
с помощью следующих тригонометрических подстановок:
для интеграла  :
: 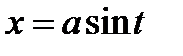 ;
;
для интеграла 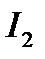 :
: 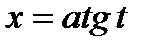 ;
;
для интеграла 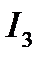 :
: 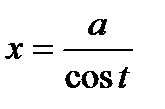 .
.
Пример.  .
.
Решение. Это интеграл второго типа. Поэтому применим подстановку 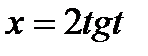 .
.
Тогда 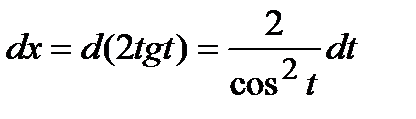 .
.
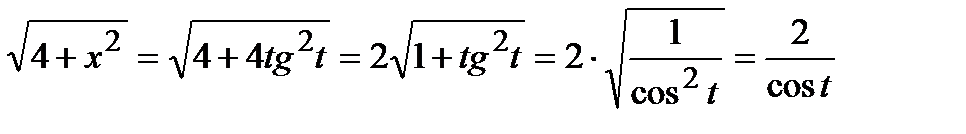 .
.
Следовательно,
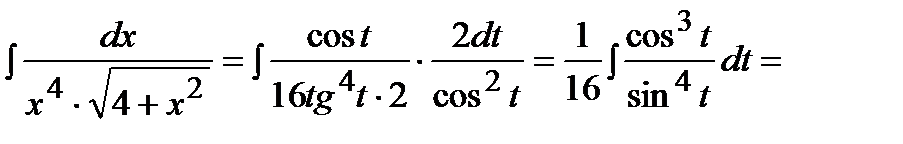
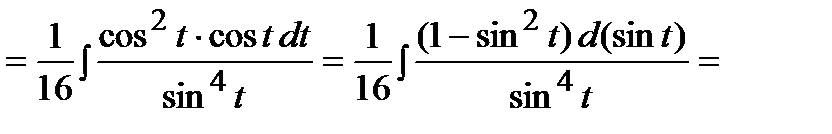
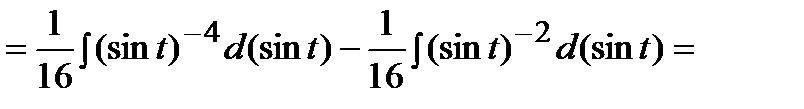
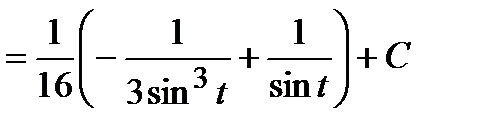 , где
, где 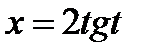 .
.
Пример . 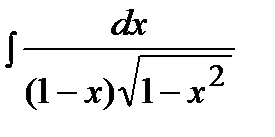 .
.
Решение. Этот интеграл первого типа и поэтому применим подстановку  .
.
Тогда 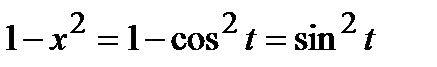 ,
, 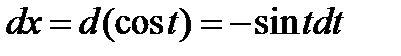 .
.
Следовательно,
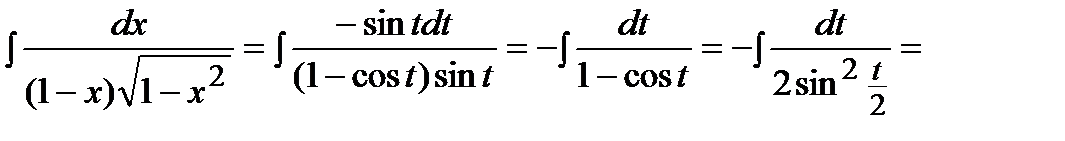
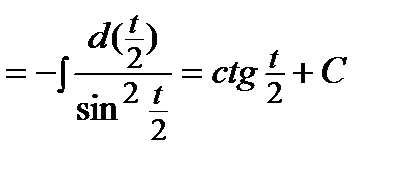 , где
, где 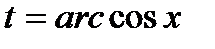 .
.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Если 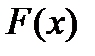 — некоторая первообразная функции
— некоторая первообразная функции 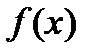 , непрерывной на отрезке
, непрерывной на отрезке  , то определенный интеграл вычисляется по формуле Ньютона – Лейбница:
, то определенный интеграл вычисляется по формуле Ньютона – Лейбница:
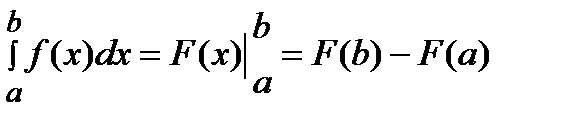 .
.
Пример. 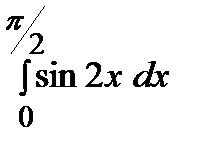 .
.
Решение.
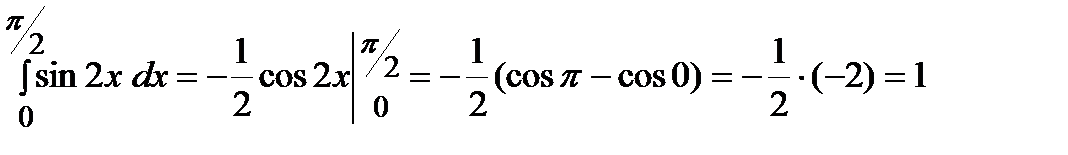 .
.
Задание 8. Замена переменной.
Пусть выполняются следующие условия:
1) функция 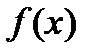 непрерывна на отрезке
непрерывна на отрезке  ;
;
2) функция 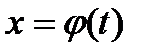 непрерывна вместе со своей производной
непрерывна вместе со своей производной 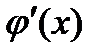 на отрезке
на отрезке 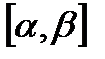 ;
;
3) 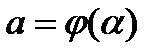 ,
, 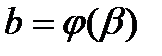 ;
;
4) функция 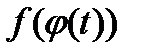 определена и непрерывна на отрезке
определена и непрерывна на отрезке 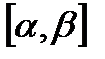 .
.
Тогда 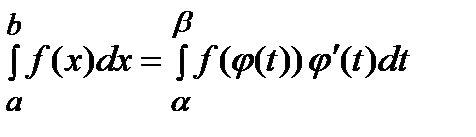 .
.
Пример. 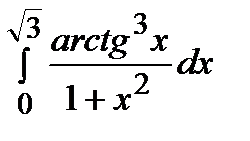 .
.
Решение.
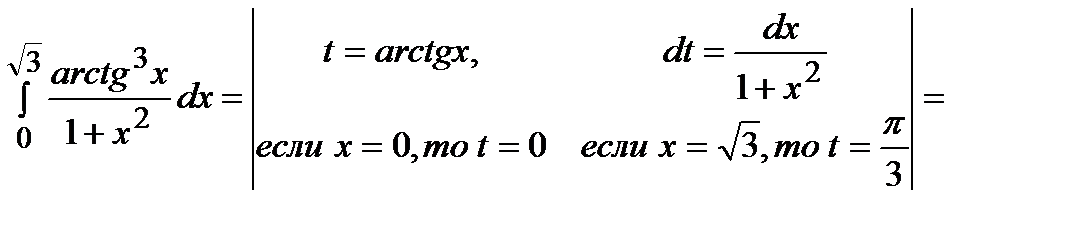
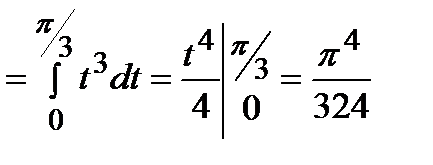 .
.
Задание 9. Интегрирование по частям.
Определенный интеграл по частям вычисляется по формуле:
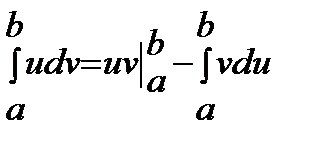 ,
,
где 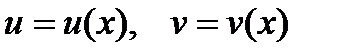 — непрерывно дифференцируемые функции на отрезке
— непрерывно дифференцируемые функции на отрезке 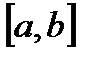 . Случаи, в которых следует применять интегрирование по частям, такие же, как в неопределенном интеграле.
. Случаи, в которых следует применять интегрирование по частям, такие же, как в неопределенном интеграле.
Пример. 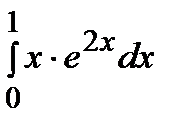 .
.
Решение.
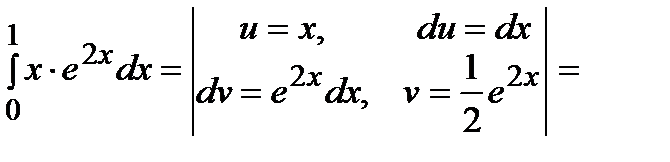
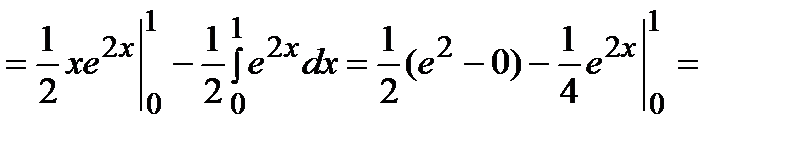
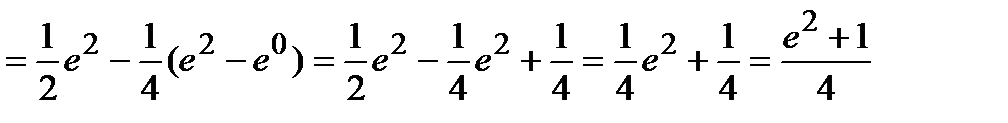 .
.
Задание 10. Вычисление площади плоской фигуры, ограниченной линиями, заданными в декартовых координатах.
В декартовой системе координат элементарной фигурой является криволинейная трапеция (рис.1), ограниченная линиями  ,
, 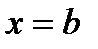 ,
, 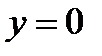 ,
, 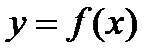 , площадь которой вычисляется по формуле:
, площадь которой вычисляется по формуле:
|
|
|
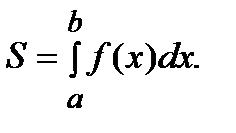
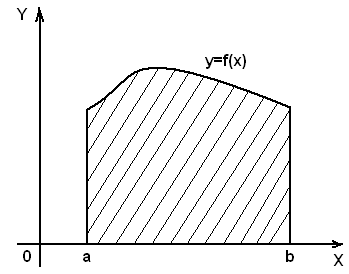
Рис.1
Площадь фигуры (рис.2) вычисляется по формуле:
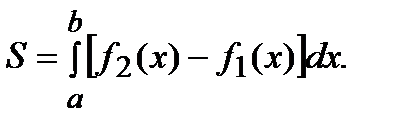

Рис.2
Пример. Найти площадь фигуры, ограниченной линиями 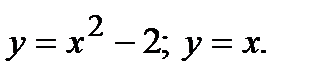
Решение. Построим чертеж к задаче (рис. 3).
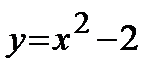 — это парабола (ветви направлены вверх, вершина находится в точке с координатами (0;-2));
— это парабола (ветви направлены вверх, вершина находится в точке с координатами (0;-2));
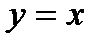 — прямая, проходящая через начало координат.
— прямая, проходящая через начало координат.
Найдем точки пересечения кривых. Для этого решим систему уравнений:  .
.
Отсюда 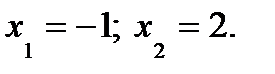
Площадь фигуры вычислим по формуле:
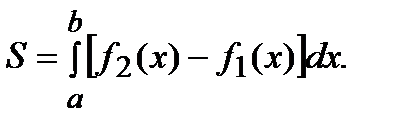
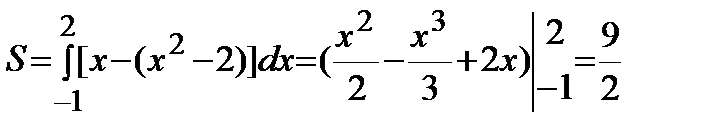 (кв.ед.).
(кв.ед.).
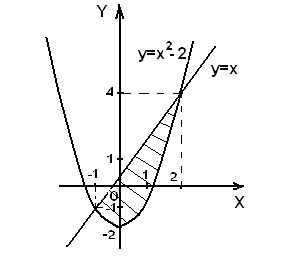
Рис. 3
Задание 11. Вычисление площади плоской фигуры, ограниченной линиями, заданными параметрическими уравнениями.
Если фигура ограничена кривой, заданной параметрическими уравнениями, то площадь вычисляется по формуле:

Пример. Вычислить площадь эллипса, заданного параметрическими уравнениями: 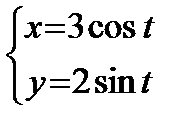 .
.
Решение. Дан эллипс с полуосями: большая — 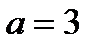 , малая —
, малая — 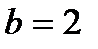 . Сделаем чертеж к задаче (рис.4).
. Сделаем чертеж к задаче (рис.4).
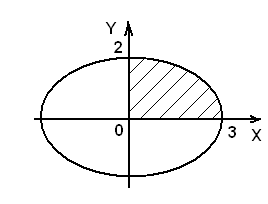
Рис. 4
В силу симметричности фигуры вычислим 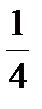 площади. Найдем пределы интегрирования:
площади. Найдем пределы интегрирования:
так как 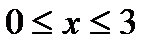 , то
, то  ;
;
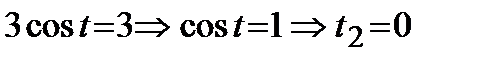 .
.
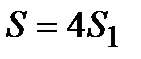 .
.
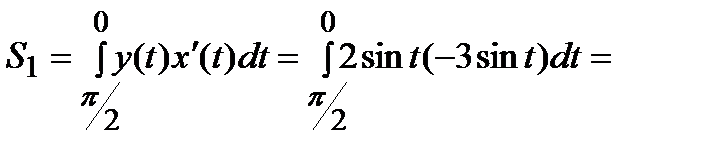
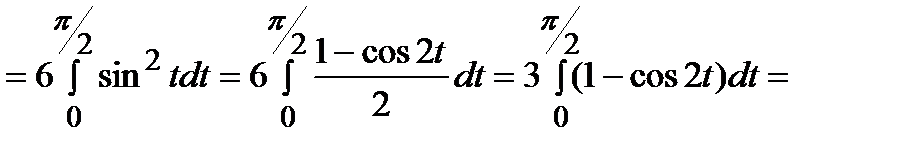
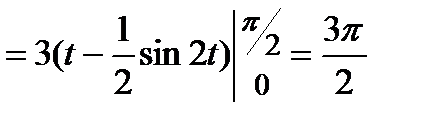 .
.
Следовательно, площадь 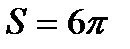 (кв.ед.).
(кв.ед.).
Задание 12. Вычисление площади плоской фигуры, ограниченной линиями, заданными в полярных координатах.
|
|
|
В полярной системе координат элементарной фигурой является криволинейный сектор (рис.5), площадь которого вычисляется по формуле:
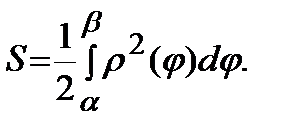
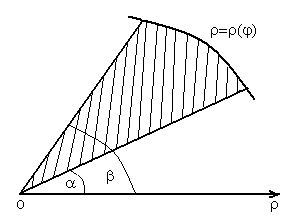
Рис. 5
Пример. Найти площадь фигуры, ограниченной линией 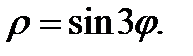
Решение. Так как 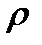 определяет расстояние до соответствующей точки, то
определяет расстояние до соответствующей точки, то  . Следовательно, область определения функции определяется неравенством
. Следовательно, область определения функции определяется неравенством 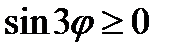 . Общее решение этого неравенства имеет вид:
. Общее решение этого неравенства имеет вид:
 где
где 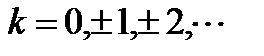 .
.
Отсюда 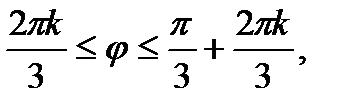
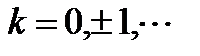 . Так как в полярной системе координат выполняются ограничения на область изменения
. Так как в полярной системе координат выполняются ограничения на область изменения 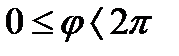 , то область допустимых значений функции
, то область допустимых значений функции 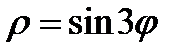 в полярной системе координат состоит из трех промежутков, описывающихся соответствующими неравенствами:
в полярной системе координат состоит из трех промежутков, описывающихся соответствующими неравенствами:
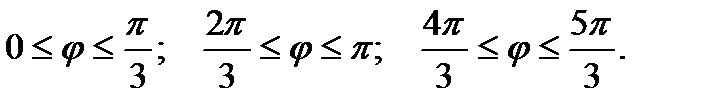
Выбрав несколько значений  из указанных промежутков, построим график функции (рис. 6).
из указанных промежутков, построим график функции (рис. 6).
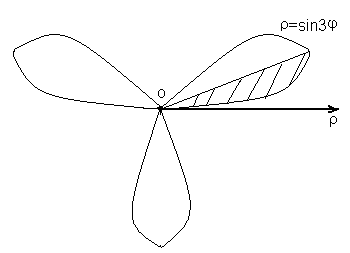
Рис.6
В силу симметричности фигуры вычислим 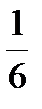 площади, где полярный угол
площади, где полярный угол 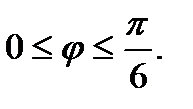
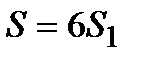 .
.

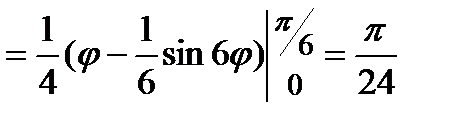 .
.
Следовательно, площадь всей фигуры 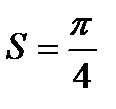 (кв.ед.).
(кв.ед.).
Дата добавления: 2019-09-13; просмотров: 185; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
