Векторы и линейные операции над ними
В геометрии вектором называют направленный отрезок 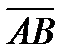 с начальной А и конечной В точками, который можно перемещать параллельно самому себе. Длиной (или модулем)
с начальной А и конечной В точками, который можно перемещать параллельно самому себе. Длиной (или модулем)  вектора
вектора 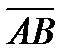 называется число, равное длине отрезка АВ, изображающего вектор.
называется число, равное длине отрезка АВ, изображающего вектор.
Векторы, параллельные одной прямой, называются коллинеарными (рис.1).

Рис.1
Векторы, параллельные одной плоскости, называются компланарными (рис.2).

Рис.2
Если вектор  изображается направленным отрезком
изображается направленным отрезком 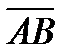 , то вектор, изображаемый направленным отрезком
, то вектор, изображаемый направленным отрезком  , называется вектором, противоположным вектору
, называется вектором, противоположным вектору 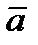 и обозначается -
и обозначается - 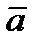 (рис.3).
(рис.3).

Рис.3
Если в прямоугольной системе координат точки А и В имеют координаты 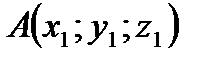 и
и 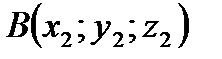 , то координаты вектора
, то координаты вектора  находятся как разности соответствующих координат конца В и начала А этого вектора, т.е.
находятся как разности соответствующих координат конца В и начала А этого вектора, т.е.
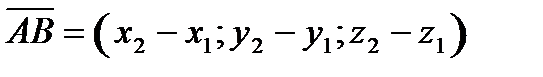 ,
,
а модуль его определяется как расстояние между двумя точками:
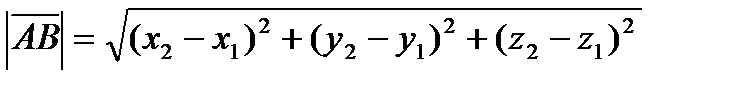 .
.
Для векторов вводятся следующие линейные операции: сложения и умножения на число. Если векторы заданы своими координатами  и
и 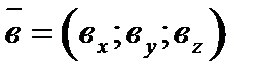 , то:
, то:
1) при сложении двух векторов их соответствующие координаты складываются: 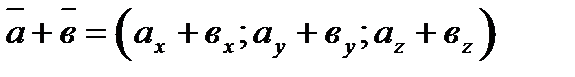 ;
;
2) при умножении вектора  на число
на число 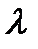 его координаты умножаются на это число:
его координаты умножаются на это число: 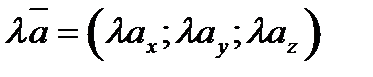 .
.
Скалярное, векторное и смешанное произведения векторов
Скалярным произведением 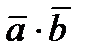 двух ненулевых векторов
двух ненулевых векторов 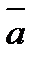 и
и 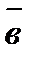 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними:  , где
, где 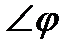 - угол между векторами
- угол между векторами 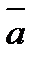 и
и 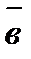 (рис.4).
(рис.4).
|
|
|

Рис.4
Пусть заданы два вектора в координатной форме 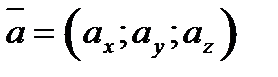 и
и 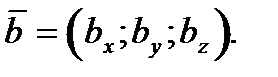
Скалярное произведение двух ненулевых векторов в координатной форме равно сумме произведений соответствующих координат этих векторов:  .
.
Косинус угла между векторами вычисляется по формуле: 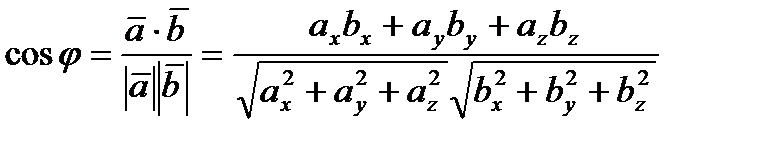 .
.
Условием перпендикулярности ненулевых векторов 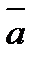 и
и 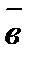 является равенство нулю их скалярного произведения:
является равенство нулю их скалярного произведения:
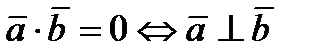 .
.
Векторным произведением двух векторов 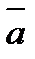 и
и 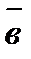 называется вектор
называется вектор  , который:
, который:
1) имеет модуль, численно равный площади параллелограмма, построенного на векторах 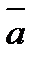 и
и 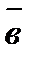 :
: 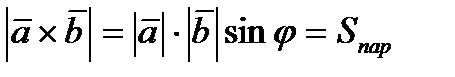 ;
;
2) перпендикулярен к плоскости этого параллелограмма;
3) направлен в такую сторону, с которой кратчайший поворот от 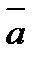 к
к 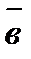 рассматривается совершающимся против часовой стрелки (такое расположение векторов
рассматривается совершающимся против часовой стрелки (такое расположение векторов  ,
, 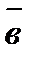 и
и  называется правой тройкой векторов) (рис.5).
называется правой тройкой векторов) (рис.5).

Рис.5
Векторное произведение ненулевых векторов 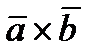 вычисляется через координаты данных векторов
вычисляется через координаты данных векторов 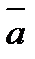 и
и 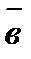
следующим образом: 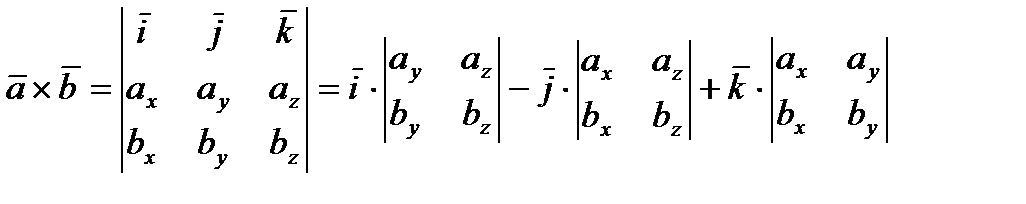
Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е. 

 ½½
½½  .
.
|
|
|
Смешанное произведение трех векторов  ,
,  и
и  , которое обозначается
, которое обозначается 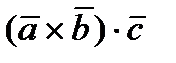 или
или  , есть скаляр, абсолютная величина которого равна объему параллелепипеда, построенного на векторах
, есть скаляр, абсолютная величина которого равна объему параллелепипеда, построенного на векторах  ,
,  и
и  , как на ребрах.
, как на ребрах.
Смешанное произведение трех векторов вычисляется в координатной форме по формуле:
 .
.
Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности:  .
.
Задача. Определить внутренние углы 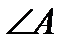 и
и 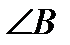 треугольника
треугольника 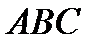 c вершинами в точках
c вершинами в точках 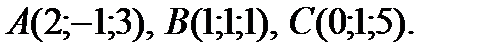
Решение . Внутренний угол 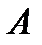 - это угол между векторами
- это угол между векторами 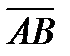 и
и 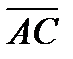 , который вычисляется через скалярное произведение векторов по формуле:
, который вычисляется через скалярное произведение векторов по формуле: 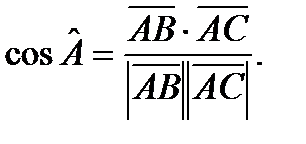
Координаты векторов:  .
.

Отсюда, 
Аналогично, находя предварительно 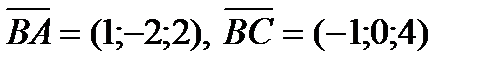 , получим
, получим
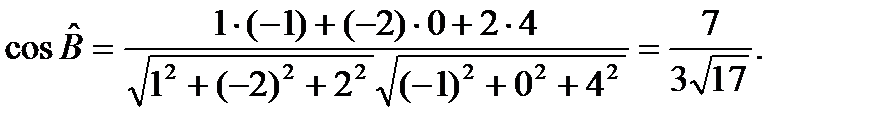
Отсюда 
Задача. Вычислить площадь треугольника с вершинами в точках  и высоту
и высоту 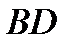 (рис.6).
(рис.6).
Решение .
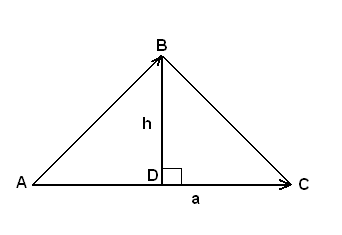
Рис.6
Найдем координаты векторов 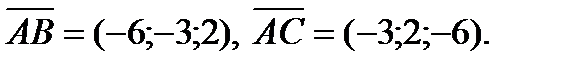 Площадь треугольника вычисляется через векторное произведение векторов по формуле:
Площадь треугольника вычисляется через векторное произведение векторов по формуле: 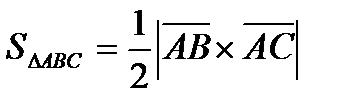 .
.
Векторное произведение
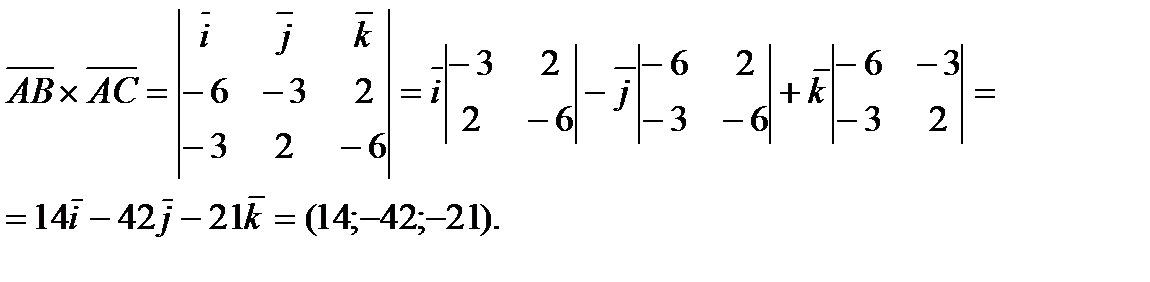
Тогда  .
.
С другой стороны 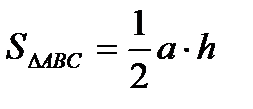 , отсюда высота
, отсюда высота 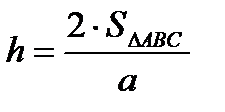 .
.
Так как  ,
,
то высота 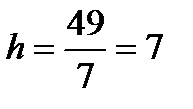 .
.
|
|
|
Задача. Вычислить объем пирамиды с вершинами в точках 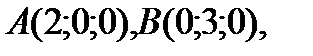
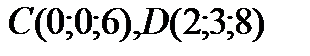 и высоту, опущенную из точки
и высоту, опущенную из точки 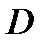 на основание
на основание 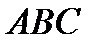 (рис.7).
(рис.7).
Решение .

Рис.7
Найдем координаты векторов 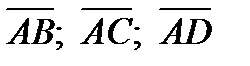 :
: 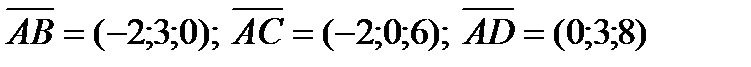 .
.
Объем пирамиды вычисляется через смешанное произведение векторов по формуле:  .
.
Смешанное произведение векторов

 .
.
Следовательно, 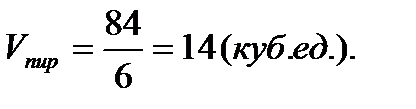
С другой стороны 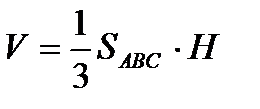 . Откуда высота пирамиды
. Откуда высота пирамиды  , где площадь треугольника
, где площадь треугольника 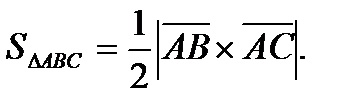
Векторное произведение
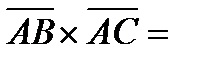
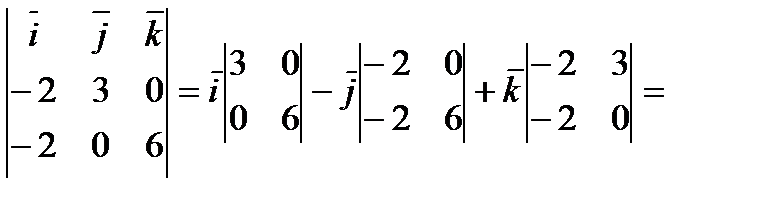
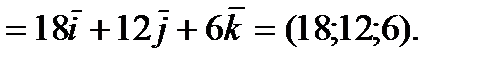
Тогда, 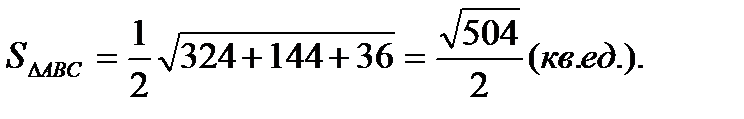
Следовательно, высота пирамиды  =
= 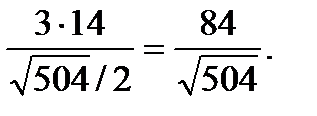
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
Уравнения плоскости 
Пусть задан вектор  , перпендикулярный к плоскости
, перпендикулярный к плоскости 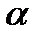 (вектор нормали) и точка
(вектор нормали) и точка 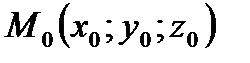 - произвольная фиксированная точка плоскости. Возьмем на плоскости
- произвольная фиксированная точка плоскости. Возьмем на плоскости  произвольную нефиксированную точку
произвольную нефиксированную точку 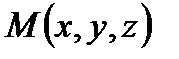 - (текущая точка) (рис.8).
- (текущая точка) (рис.8).
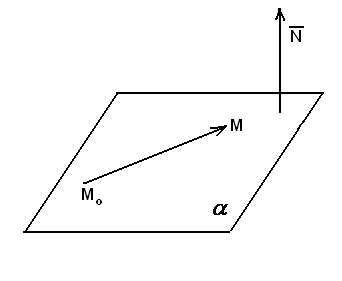
Рис.8
Вектор 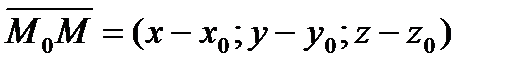 , лежащий в плоскости
, лежащий в плоскости  , перпендикулярен вектору нормали
, перпендикулярен вектору нормали  , значит их скалярное произведение
, значит их скалярное произведение 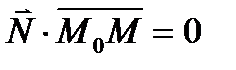 , следовательно
, следовательно
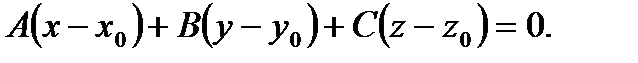
Полученное уравнение – уравнение плоскости, проходящей через точку 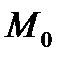 , перпендикулярно вектору
, перпендикулярно вектору 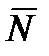 .
.
Пример. Составить уравнение плоскости, проходящей через точку 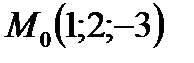 и перпендикулярно вектору
и перпендикулярно вектору 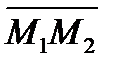 , если
, если 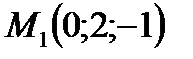 ,
, 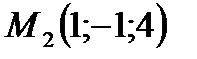 (рис.9).
(рис.9).
Решение. Пусть 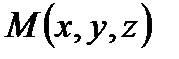 - текущая точка искомой плоскости
- текущая точка искомой плоскости 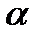 . Найдем координаты векторов
. Найдем координаты векторов
|
|
|
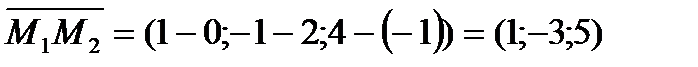
 .
.
Вектор  принадлежит плоскости
принадлежит плоскости 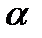 и перпендикулярен вектору
и перпендикулярен вектору  , значит их скалярное произведение
, значит их скалярное произведение 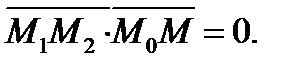
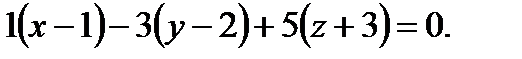
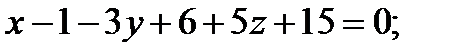
 - уравнение плоскости
- уравнение плоскости 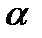 .
.
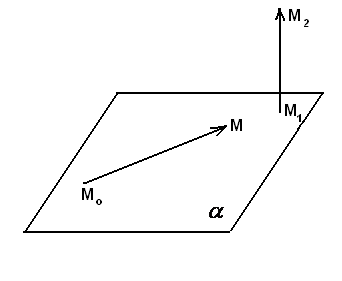
Рис.9
Рассмотрим плоскость, проходящую через три точки, не лежащие на одной прямой: 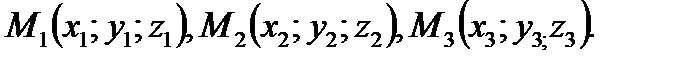 - (рис.10). Точка
- (рис.10). Точка 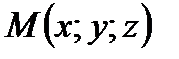 - текущая точка плоскости.
- текущая точка плоскости.

Рис.10
Три вектора:
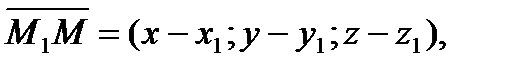 ,
, 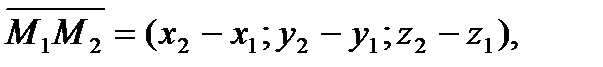
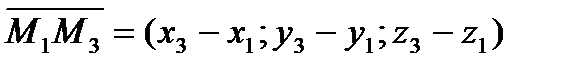
лежат в одной плоскости, значит компланарны, и их смешанное произведение равно нулю: 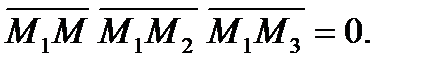
Запишем смешанное произведение в координатной форме, получим:
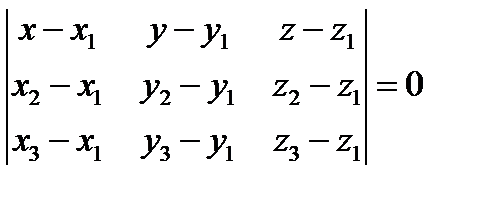 - уравнение плоскости, проходящей
- уравнение плоскости, проходящей
через три точки.
Пример. Найти уравнение плоскости, проходящей через три точки
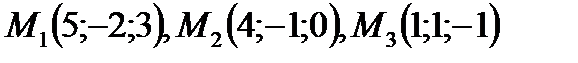 (рис.11).
(рис.11).

Рис.11
Решение. Пусть точка  - текущая точка плоскости. Найдем координаты трех компланарных векторов:
- текущая точка плоскости. Найдем координаты трех компланарных векторов: 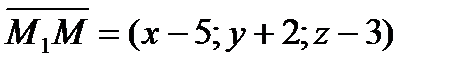 ,
, 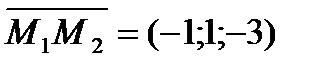 ,
, 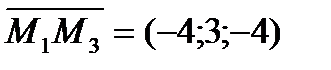 .
.
Смешанное произведение векторов равно нулю: 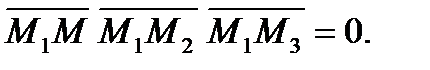
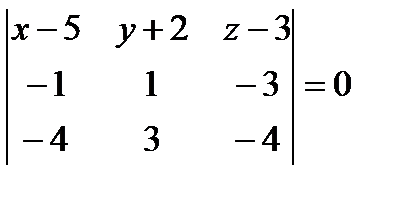
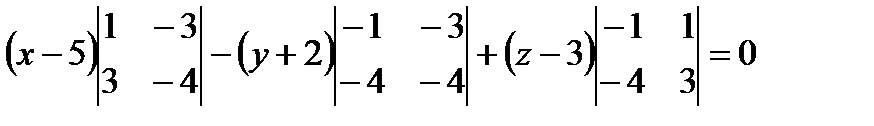
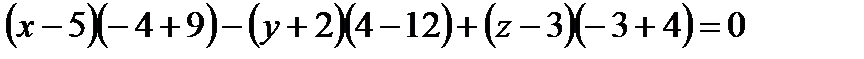
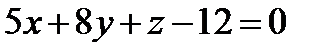 - уравнение плоскости
- уравнение плоскости 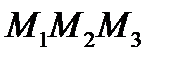 .
.
Пусть плоскость  задана общим уравнением
задана общим уравнением  .
.
Расстояние от точки  до плоскости
до плоскости  (рис12) вычисляют по формуле
(рис12) вычисляют по формуле 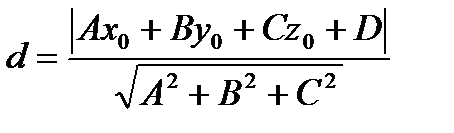 .
.

Рис.12
Пример. Найти расстояние от точки 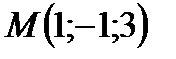 до плоскости
до плоскости 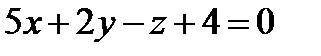 .
.
Решение. Воспользуемся формулой расстояния от точки до плоскости, получим:
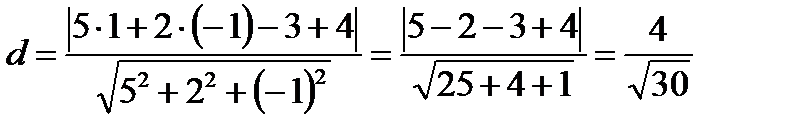 .
.
Угол между плоскостями равен углу 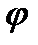 между их векторами нормалей (рис.13).
между их векторами нормалей (рис.13).
Пусть даны две плоскости:
плоскость 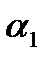 с нормалью
с нормалью 
плоскость 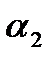 с нормалью
с нормалью 

Рис.13
Косинус угла между плоскостями вычисляется по формуле:
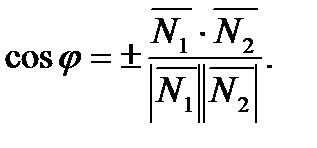
Пример. Найти угол между плоскостями
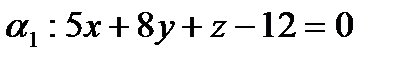 ;
;
 .
.
Решение. Векторы нормалей имеют координаты: 

 Отсюда,
Отсюда,

Уравнения прямой в пространстве
Рассмотрим в пространстве прямую a, проходящую через точку 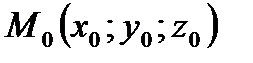 параллельно вектору
параллельно вектору 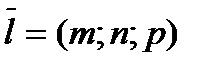 , который называется направляющим вектором прямой а (рис.14).
, который называется направляющим вектором прямой а (рис.14).
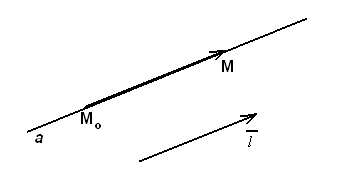
Рис.14
Пусть точка  - текущая точка прямой. Вектор
- текущая точка прямой. Вектор 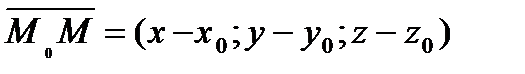 лежит на прямой и коллинеарен вектору
лежит на прямой и коллинеарен вектору  . Из условия коллинеарности двух векторов, имеем:
. Из условия коллинеарности двух векторов, имеем: 
Эти уравнения - канонические уравнения прямой в пространстве.
Если в канонических уравнениях ввести параметр t :  , получим параметрические уравнения прямой:
, получим параметрические уравнения прямой:
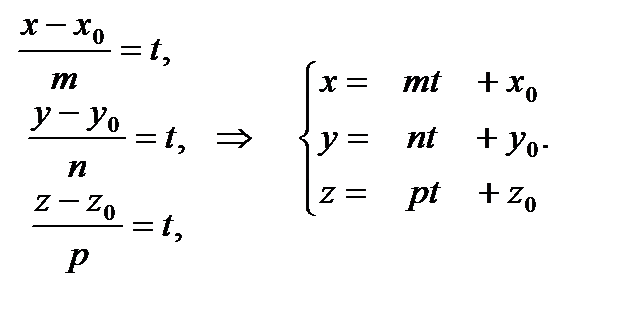
Прямую можно задать как линию пересечения двух плоскостей (рис.15):
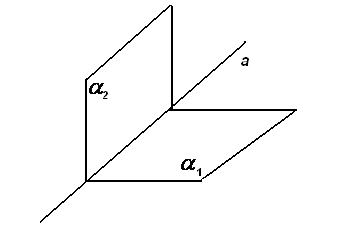
Рис.15
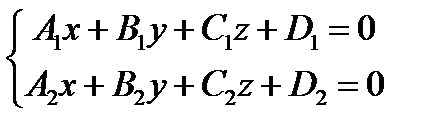 - общие уравнения прямой в пространстве.
- общие уравнения прямой в пространстве.
Уравнения прямой, проходящей через две точки  и
и 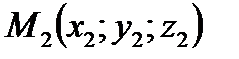 :
: 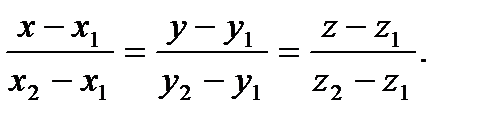
Угол между прямыми равен острому углу между их направляющими векторами (рис.16) и вычисляется по формуле:
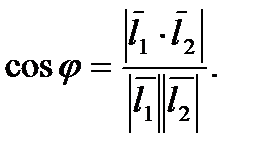
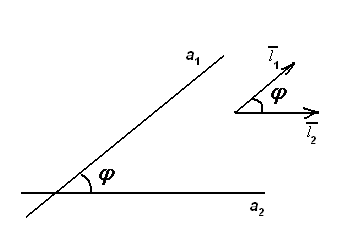
Рис.16
Пример. Прямая  задана общими уравнениями
задана общими уравнениями
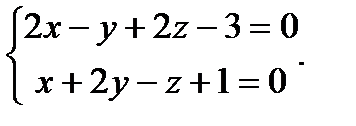
а) Написать для этой прямой канонические и параметрические уравнения;
б) Найти угол между прямой  и прямой
и прямой  ,заданной уравнениями
,заданной уравнениями

Решение.
а)Выберем одну из точек, через которую пройдет указанная прямая, заданная пересечением плоскостей. Исходная система имеет бесчисленное множество решений, одно из которых получим придавая одной из переменных конкретное значение. Пусть 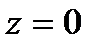 , тогда значения других неизвестных находим из системы
, тогда значения других неизвестных находим из системы 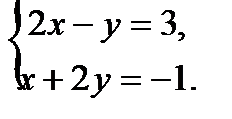
Решением этой системы является пара чисел 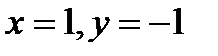 .
.
В результате получим точку 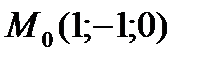 , через которую проходит искомая прямая. В качестве направляющего вектора прямой можно взять вектор
, через которую проходит искомая прямая. В качестве направляющего вектора прямой можно взять вектор 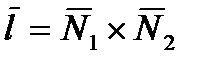 , где
, где  ,
, 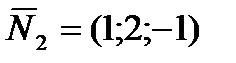 - нормальные векторы плоскостей, линией пересечения которых является прямая. Таким образом,
- нормальные векторы плоскостей, линией пересечения которых является прямая. Таким образом,
 .
.
Запишем канонические уравнения прямой  :
: 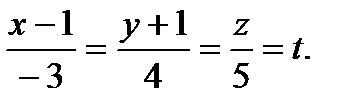
Получим из канонических параметрические уравнения прямой: 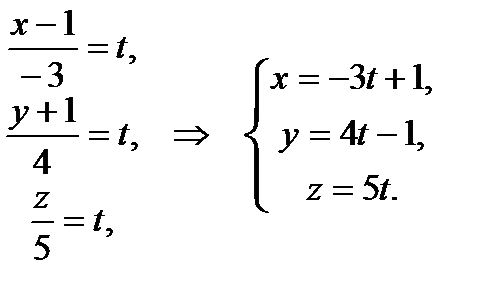
б) Направляющий вектор прямой  , направляющий вектор прямой
, направляющий вектор прямой 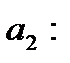
 Угол между прямыми
Угол между прямыми 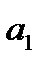 и
и 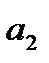 равен острому углу между их направляющими векторами:
равен острому углу между их направляющими векторами:
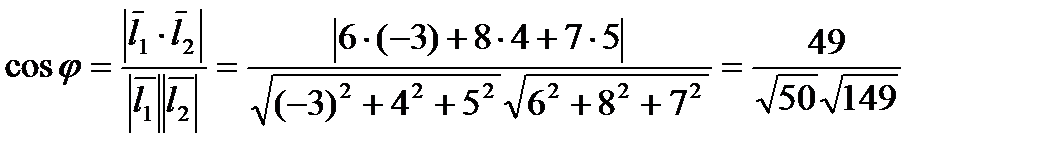
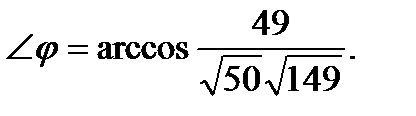
Угол между прямой и плоскостью
Пусть заданы прямая a и плоскость  (рис.17):
(рис.17):
Прямая 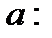
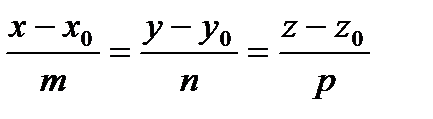 c направляющим вектором
c направляющим вектором 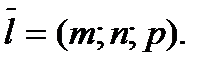
Плоскость 
 с вектором нормали
с вектором нормали 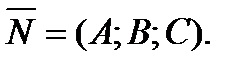
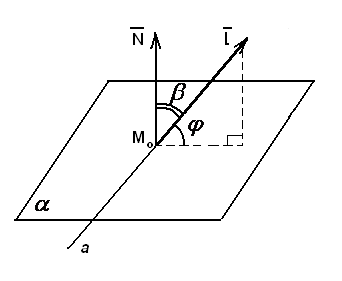
Рис.17
Угол 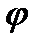 между прямой а и плоскостью
между прямой а и плоскостью 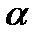 вычисляется по формуле:
вычисляется по формуле: 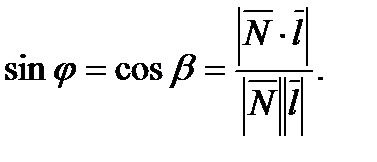
Чтобы найти точку пересечения прямой и плоскости, нужно параметрические уравнения прямой 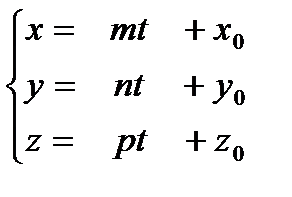 подставить в уравнение плоскости
подставить в уравнение плоскости  и найти параметр
и найти параметр 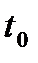 , соответствующий точке пересечения.
, соответствующий точке пересечения.
Пример. Найти а) угол между прямой и плоскостью;
б) точку пересечения прямой и плоскости.
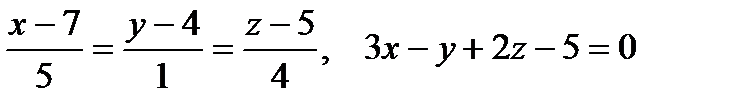 .
.
Решение. 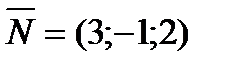 - нормаль к плоскости;
- нормаль к плоскости; 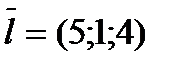 - направляющий вектор прямой.
- направляющий вектор прямой.
а) 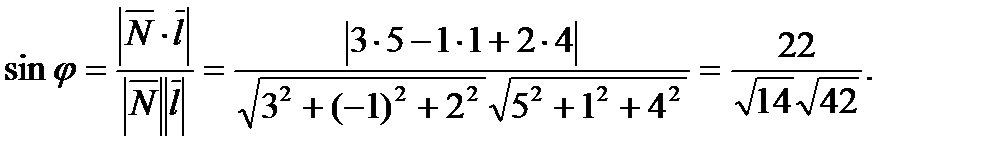
Отсюда, 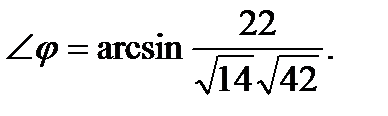
б) Подставим параметрические уравнения прямой  в уравнение плоскости
в уравнение плоскости 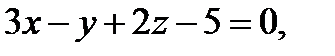
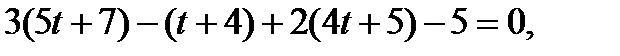
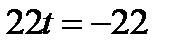 ,
,  - параметр точки пересечения прямой и плоскости.
- параметр точки пересечения прямой и плоскости.
Подставим значение параметра 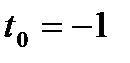 в параметрические уравнения, получим:
в параметрические уравнения, получим: 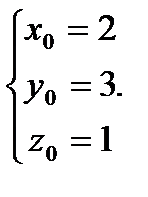 Координаты точки пересечения
Координаты точки пересечения 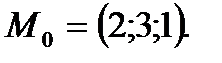
Уравнение прямой на плоскости
Каноническое уравнение прямой на плоскости:  , где
, где  - направляющий вектор прямой.
- направляющий вектор прямой.
Общее уравнение прямой на плоскости: 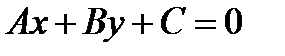 ,
,
где 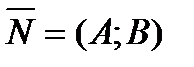 - вектор нормали прямой.
- вектор нормали прямой.
Уравнение прямой с угловым коэффициентом 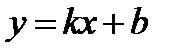 (рис.18), где
(рис.18), где  - угловой коэффициент прямой; угол
- угловой коэффициент прямой; угол 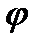 – угол между прямой и осью ОХ;
– угол между прямой и осью ОХ;
b – отрезок, отсекаемый прямой на оси OY.
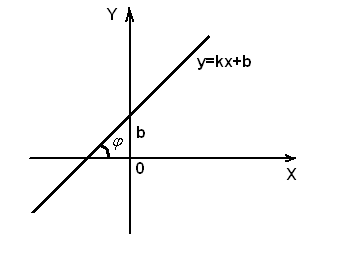
Рис.18
Уравнение прямой, проходящей через две точки  и
и 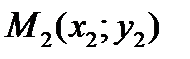 :
: 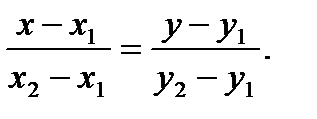
Пример Даны точки А(2;5), В(-3;1), С(5;2).
Найти:  а) уравнение медианы AD;
а) уравнение медианы AD;
б) уравнение высоты AE;
в) угол между медианой AD и высотой AE;
г) уравнение прямой, проходящей через точку С, параллельно прямой АВ (рис19).
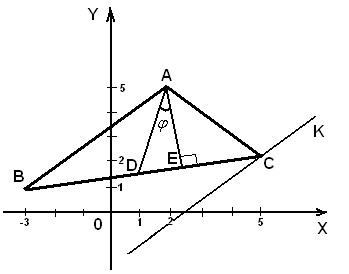
Рис.19
Решение.
а) Точка D - середина отрезка ВС, найдем ее координаты: 
Прямая AD проходит через две точки. Её уравнение имеет вид: 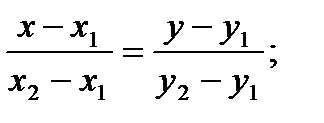
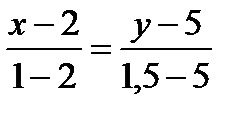 ;
;  ;
;
 - уравнение прямой AD .
- уравнение прямой AD .
б) Высота перпендикулярна ВС. Пусть точка Е имеет координаты 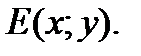 Тогда векторы
Тогда векторы 
следовательно, их скалярное произведение 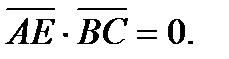
 - уравнение высоты АЕ.
- уравнение высоты АЕ.
в) Угол 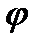 между медианой AD и высотой АЕ – это угол между их векторами нормалей
между медианой AD и высотой АЕ – это угол между их векторами нормалей 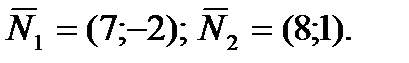
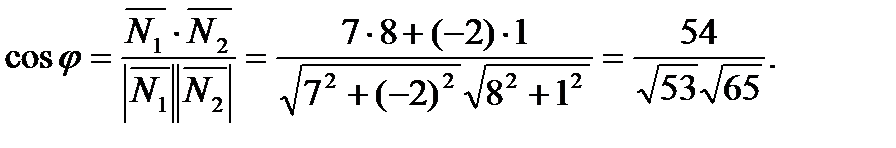
Отсюда, 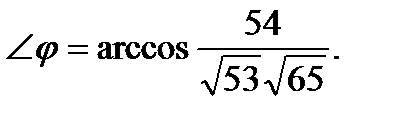
г) Прямая СК параллельна прямой АВ. Пусть точка K имеет координаты 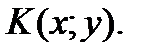 Тогда векторы
Тогда векторы 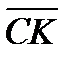 и
и  коллинеарны.
коллинеарны.
Отсюда, 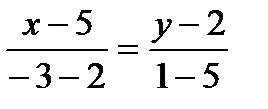 ;
; 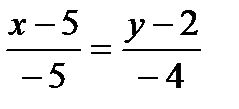 ;
; 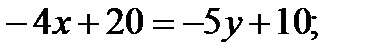
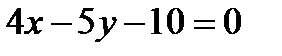 - уравнение прямой СК, параллельной АВ.
- уравнение прямой СК, параллельной АВ.
Дата добавления: 2019-09-13; просмотров: 258; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
