Лекция 6. Переходные процессы в линейных электрических цепях и методы их анализа 4 страница

⇐ ПредыдущаяСтр 20 из 35Следующая ⇒

будет

наибольшее и в начальный момент времени равное амплитуде

U Cm

установившегося

напряжения. Начальное значение свободного тока при этом будет (- U Cm R). Если

R << X C , то в начальный момент времени произойдет скачкообразное увеличение тока

в цепи, намного превосходящее амплитуду

I m . Однако такой большой ток будет

протекать незначительную часть периода, так как

R = 2p t

<< 1,

X C T

и, следовательно,

t << T . Максимальное значение напряжения u C

в переходном

процессе не превышает удвоенной амплитуды установившемся режиме.

U Cm

напряжения на ёмкости в

6.9 Переходные процессы в цепи постоянного тока при последовательном соединении резистора, индуктивной катушки и конденсатора

Рассмотрим переходные процессы в цепи, состоящей из последовательно включенных участков с сопротивлением R , индуктивностью L и ёмкостью C (рисунок 6.9). Исследуем частный, но практически важный случай переходного режима, возникающего при отключении конденсатора от источника постоянного напряжения и подключении его к ветви с активным сопротивлением R и индуктивностью L , т.е. режим разряда конденсатора в R , L – цепь (в индуктивную катушку).

На основании 2-го закона Кирхгофа запишем уравнение для напряжений в цепи после коммутации:

u R + u L + u C = 0 .

Учитывая, что

u R = Ri ,

u = L di

L dt

и i = C du C

, получим дифференциальное

уравнение 2-го порядка

D 2u du

LC C + RC C + u C = 0 . (6.50)

dt 2 dt

Разделим обе части уравнения (6.50) на произведение LC :

D 2u R du 1

C + C +

u C = 0

(6.51)

dt 2 L dt LC

и для удобства анализа введем обозначения

d = R ,

w0 =

1 , (6.52)

где d — коэффициент затухания, w0

— угловая частота незатухающих колебаний.

Из (6.51), (6.52) получим уравнение

d 2u dt 2

+ 2d

du C dt

+ w 2u = 0 . (6.53)

0 C

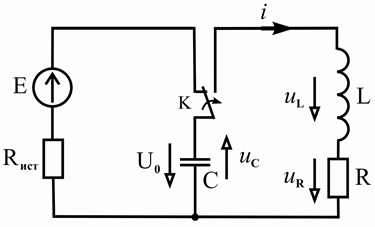
Рисунок 6.9 – Схема замещения цепи при подключении заряженного конденсатора к индуктивной катушке

Дифференциальное уравнение (6.53), описывающее переходной процесс в рассматриваемой цепи, является однородным уравнением, поэтому его общее решение

существует в форме свободной составляющей напряжения

u C = u Cсв , структура которой

однозначно определяется корнями характеристического уравнения.

Характеристическое уравнение согласно (6.53) имеет вид

l2 + 2dl + w 2 = 0 . (6.54)

В зависимости от соотношения параметров цепи (величин R , L и C ) корни характеристического уравнения (6.54) могут быть:

1) вещественными и различными, если дискриминант больше нуля, т.е. d > w0

или

R > 2r , где r = ;

2) вещественными и равными, если дискриминант равен нулю, т.е.

R = 2r ;

3) комплексно-сопряженными, если дискриминант меньше нуля, т.е.

R < 2r .

d = w0

d < w0

или или

Характер переходного процесса в данной цепи будет существенно различным в

зависимости от того, являются ли корни характеристического уравнения вещественными или комплексными.

6.9.1 Апериодический разряд конденсатора

Пусть корни характеристического уравнения (6.54) вещественные и различные:

l1 = -d +

, l2

= -d -

. (6.55)

В этом случае общее решение однородного уравнения (6.53) имеет вид

u = A e ^l1t + A e ^l2t , (6.56)

где произвольные постоянные

C 1 2

A1 и A2 определяются из начальных условий

неизменности тока в катушке и напряжения на зажимах конденсатора в момент

коммутации: i L (0- ) = i L (0+ ), u C (0- ) =u C (0+ ), т.е. из начальных условий, полученных на

основании 1-го и 2- го законов коммутации.

Из формулы (6.56) получаем выражение для силы тока в цепи:

i = C du C = C(l A e ^l1t + l A e ^l2t ). (6.57)

dt 1 1 2 2

Так как в докоммутационном режиме i(0- ) = i L (0- ) = 0

и u C (0- ) = U0 , где U0 —

первоначальное напряжение на конденсаторе ( 0 < U0 £ E ), то из (6.56) и (6.57) получим

два уравнения для определения постоянных интегрирования A1 и

A2 :

A1 + A2 = U0 и l1A1 + l2 A2 = 0 .

Совместное решение этих уравнений даст

A = -

U0l2 ,

A = U0l1

. (6.58)

1 - l

1 - l2

Подставляя (6.58) в (6.56) и (6.57), найдем формулы, определяющие напряжение на конденсаторе и ток в цепи в любой момент времени после коммутации:

u = - U0 (l e ^l1t - l e ^l2t ),

i = - ( U0

)(e ^l1t - e ^l2t ). (6.59)

C - l 2 1

L l1 - l2

Напряжение на индуктивности равно:

u = L di = - U0 (l e ^l1t - l e ^l2t ). (6.60)

L dt l - l

1 2

Анализ корней (6.55) характеристического уравнения приводит к неравенствам:

l1 < 0 и l2 < 0 .

Это означает, что каждая из найденных величин u C , i и u L

состоит из 2-х слагаемых,

затухающих по экспонентам с коэффициентами затухания

l1 и l2 . Графики изменения

величин

u C , i и u L

в переходном режиме, построенные согласно выражениям (6.59) и

(6.60), приведены на рисунке 6.10.

Из рисунка 6.10 видно, что напряжение u C

на конденсаторе монотонно

уменьшается от U0

до нуля, не меняя знака. Такой разряд конденсатора, при котором

энергия его электрического поля непрерывно убывает и не происходит процесса перезарядки, называется апериодическим разрядом.

Ток i при апериодическом разряде (см. рисунок 6.10) возрастает от нуля до некоторого максимума при t = t1 , а затем убывает, асимптотически стремясь к нулю.

Напряжение u L на индуктивности начинает свое изменение со значения

u L (0+ ) = -U0 и убывает до нуля ( t = t1 ), а затем, изменяя знак, возрастает до максимума

( t = t2 ) и далее асимптотически стремится к нулю.

В момент времени

t1 напряжение на конденсаторе u C

проходит точку перегиба,

ток i — свой максимум, а напряжение u L

на индуктивности равно нулю. Перегиб

кривой тока i и максимум u L также имеет место в один и тот же момент времени t2 .

Рисунок 6.10 – Временная диаграмма токов и напряжений в цепи при апериодическом разряде конденсатора

Из рисунка 6.10 следует, что мгновенная мощность

p C всегда отрицательна:

p C = u C i < 0

и, следовательно, конденсатор в течение всего переходного процесса

отдает свою энергию. Энергия конденсатора непрерывно расходуется на покрытие

тепловых потерь в сопротивлении цепи, но, кроме того, в интервале времени от 0 до

t1 ,

когда

p L = u L i > 0 , конденсатор расходует энергию и на создание магнитного поля, т.е.

часть энергии, запасенной в его электрическом поле, переходит в энергию магнитного поля индуктивности. От момента t1 до конца процесса тепловые потери покрываются не только за счет энергии электрического поля, но и за счет энергии магнитного поля, запас

которой создан в интервале времени от 0 до

t1 . Когда вся энергия заряженного

конденсатора превратится в тепло, процесс в цепи закончится.

6.9.2 Критический разряд конденсатора

Пусть корни характеристического уравнения (6.54) вещественные и равные:

l1 = l2 = -d . (6.61)

В этом случае общее решение однородного уравнения (6.53) имеет вид

u C = (A1 + A t )e , (6.62)

-d t

а сила тока в цепи определяется выражением

i = C du C

= C(- d A1

+ A2

- d A t )e-d t . (6.63)

Для определения произвольных постоянных A1 и A2 используем начальные

условия, согласно которым i(0- ) = i L (0- ) = 0 и u C (0- ) = U0 . Из (6.62) и (6.63) тогда

получим два следующих уравнения:

A1 = U0 и

C(- d A1 + A2 ) = 0 .

Совместное решение этих уравнений даст

A1 = U0 , A2 = d U0 . (6.64)

Подставляя (6.64) в (6.62) и (6.63), найдем формулы, определяющие напряжение на конденсаторе и ток в цепи в любой момент времени после коммутации:

u C = U0

(d t + 1)e-d t ,

i = - U0 te-d t . (6.65)

Напряжение на индуктивности равно:

u = L di = U

L dt 0

(d t -1)e-d t . (6.66)

Если построить графики изменения величин

u C , i и u L

в переходном режиме

согласно выражениям (6.65), (6.66), то они окажутся аналогичными кривым

u C , i и

u L ,

изображенным на рисунке 6.10. Все переменные будут только быстрее нарастать и быстрее убывать, чем в первом случае; конденсатор будет непрерывно разряжаться, а напряжение на нем будет монотонно убывать, не меняя своего знака. Следовательно, и в данном случае имеет место апериодический разряд. Этот предельный случай апериодического разряда называют еще критическим разрядом конденсатора.

Значение R кр = 2r , при котором наблюдается критический случай

апериодического разряда, называется критическим сопротивлением последовательного контура.

6.9.3 Колебательный разряд конденсатора

Пусть корни характеристического уравнения (6.54) комплексно-сопряженные: