Теорема, обратная теореме Виета
Если внимательно посмотреть на вторую формулировку теоремы Виета, то можно увидеть, что для корней x₁ и x₂приведенного квадратного уравнения 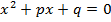 будут справедливы соотношения x₁+x₂=−p, x₁⋅x₂=q. Из этих соотношений x₁+x₂=−p, x₁⋅x₂=q следует, что x₁ и x₂ – это корни квадратного уравнения
будут справедливы соотношения x₁+x₂=−p, x₁⋅x₂=q. Из этих соотношений x₁+x₂=−p, x₁⋅x₂=q следует, что x₁ и x₂ – это корни квадратного уравнения 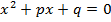 . Так приходим к утверждению, которое является обратным теореме Виета.
. Так приходим к утверждению, которое является обратным теореме Виета.
Теорема 3
Если числа x₁ и x₂ таковы, что x₁+x₂=−p и x₁⋅x₂=q, то x₁ и x₂ являются корнями приведенного квадратного уравнения 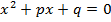 .
.
Доказательство 3
Замена коэффициентов p и q на их выражение через x₁ и x₂ позволяет преобразовать уравнение 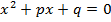 в равносильное ему
в равносильное ему 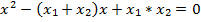 .
.
Если в полученное уравнение подставить число x₁ вместо x, то мы получим равенство 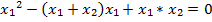 . Это равенство при любых x₁ и x₂ превращается в верное числовое равенство 0=0, так как
. Это равенство при любых x₁ и x₂ превращается в верное числовое равенство 0=0, так как 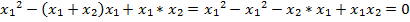 . Это значит, что x₁ – корень уравнения
. Это значит, что x₁ – корень уравнения 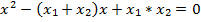 , и что x₁ также является корнем равносильного ему уравнения
, и что x₁ также является корнем равносильного ему уравнения 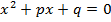 ..
..
Подстановка в уравнение 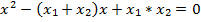 числа x₂вместо x позволяет получить равенство
числа x₂вместо x позволяет получить равенство 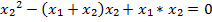 . Это равенство можно считать верным, так как
. Это равенство можно считать верным, так как 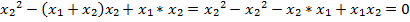 . Получается, что x₂ является корнем уравнения
. Получается, что x₂ является корнем уравнения 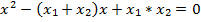 , а значит, и уравнения
, а значит, и уравнения 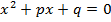 .
.
Теорема, обратная теореме Виета, доказана.
Формулы Виета
Существует ряд формул, которые применимы для осуществления действий с корнями и коэффициентами не только квадратных, но также кубических и других видов уравнений. Их называют формулами Виета.
|
|
|
Для алгебраического уравнения степени n вида  считается, что уравнение имеет n действительных корней
считается, что уравнение имеет n действительных корней 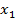 ,
, 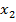 , …,
, …, 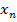 , среди которых могут быть совпадающие:
, среди которых могут быть совпадающие:
 ,
,
x₁x₂+ 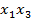 +…+
+…+ 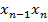 =
= 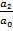 ,
,
 +
+ 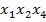 +…+
+…+  =-
=- 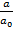 ,
,
…
 =
= 
Получить формулы Виета помогают:
- теорема о разложении многочлена на линейные множители;
- определение равных многочленов через равенство всех их соответствующих коэффициентов.
Так, многочлен 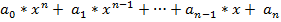 и его разложение на линейные множители вида
и его разложение на линейные множители вида 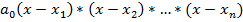 равны.
равны.
Если раскрыть скобки в последнем произведении и приравнять соответствующие коэффициенты, то получим формулы Виета. Приняв n=2, получаем формулу Виета для квадратного уравнения:  ,
, 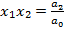 .
.
Определение 2
Формула Виета для кубического уравнения:
 ,
,
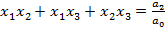 ,
,
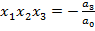 .
.
Левая часть записи формул Виета содержит так называемые элементарные симметрические многочлены.
Определение 3
Формула Виета для уравнения четвертой степени:

Практическая часть
Задание 1
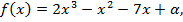

Найти 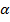
Решение
По теореме Виета для многочлена  с корнями
с корнями 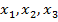 над полем комплексных чисел
над полем комплексных чисел 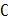 выполнены следующие соотношения:
выполнены следующие соотношения: 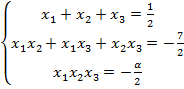
Решая систему, находим: 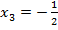 ,
, 
Подставляя эти равенства в третье уравнение системы, получим 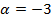
Ответ: -3
Если нам известна сумма двух корней мн-на, можно найти свободный член.
|
|
|
 ,
, 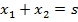
По теореме Виета выполнены рав-ва: 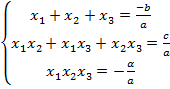
Подставляя в первое уравнение системы, получаем 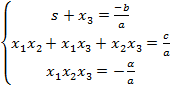
Выражая из первого уравнения системы 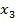 и подставляя
и подставляя 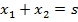 во второе уравнение системы, получаем
во второе уравнение системы, получаем 
Выражая 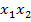 из второго уравнения системы и подставляя в третье, получаем:
из второго уравнения системы и подставляя в третье, получаем:
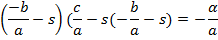
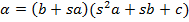
Задание 2
Найти 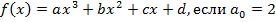
Решение
По теореме Виета для многочлена  с корнями
с корнями 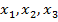 над полем комплексных чисел
над полем комплексных чисел 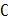 выполнены следующие соотношения:
выполнены следующие соотношения:
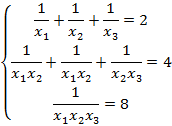
Решая систему, находим d 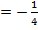 , c=
, c= 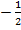 , b=-1
, b=-1
Подставляя коэффициенты, получим многочлен 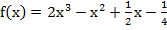
Ответ: 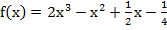
Дата добавления: 2019-07-15; просмотров: 128; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
