Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
Рассм. задачу 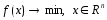 . Пусть выбрано некоторое
. Пусть выбрано некоторое 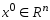 начальное приближение. И методом покоординатного спуска было получено приближение
начальное приближение. И методом покоординатного спуска было получено приближение 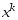 . Ч/з
. Ч/з 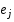 ,
, 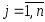 , обозначим координатные вектора
, обозначим координатные вектора 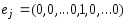 (1 наj-ом месте). Положим
(1 наj-ом месте). Положим 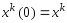 и для
и для 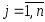
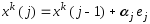 , где
, где 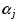 определяется из условия
определяется из условия 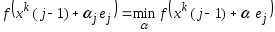 . И след. приближение
. И след. приближение 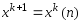 , если для некоторого
, если для некоторого 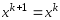 , то процесс вычисления заканчивают, А т
, то процесс вычисления заканчивают, А т 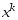 считают приближением к точке минимума.
считают приближением к точке минимума.
Данный метод хорошо подходит для задач с параллепипедными ограничениями,
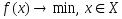 ,
,  . В этом случае при решении вспомагательной задачи минимизации
. В этом случае при решении вспомагательной задачи минимизации 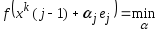 ,
, 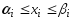 .
.
на альфа накладываются ограничения, не позволяющие точкам х выходить за пределы мн-ва Х
Сходимость метода скорейшего спуска.
Рассм. задачу 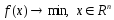 (1). Пусть в (1) ф-ция f(x) непрерывно дифференцируема, ограничена снизу на мн-ве
(1). Пусть в (1) ф-ция f(x) непрерывно дифференцируема, ограничена снизу на мн-ве 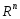 , ее градиент уд.векторному усл. Липшица с константой L, то есть
, ее градиент уд.векторному усл. Липшица с константой L, то есть 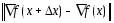 для всex
для всex 
Тогда при любом начальном приближении 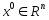 итерационный процесс метода скорейшего спуска является релаксационным,то есть уд.нер-ву
итерационный процесс метода скорейшего спуска является релаксационным,то есть уд.нер-ву 
обладает св-вом 
Если дополнительно предположить, что мн-во 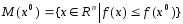 ограничено, то посл-ность {xk} сходится к непустому мн-ву S*стационарных точек ф-ции f(x)
ограничено, то посл-ность {xk} сходится к непустому мн-ву S*стационарных точек ф-ции f(x)
Если кроме того, f(x) выпукла на 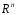 то посл-ность{xk} явл. минимизирующей и сходится к непустому мн-ву X* решений задачи.
то посл-ность{xk} явл. минимизирующей и сходится к непустому мн-ву X* решений задачи.
Основные задачи ЛП. Правила сведения задачи ЛП к канонической форме. Геометрическая интерпретация задачи ЛП. Понятие угловой точки множества.
В ЛП выделяют 2 основных формы задачи:
|
|
|
- Каноническая форма ЗЛП
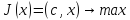
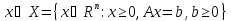
2) Нормальная форма ЗЛП 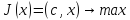
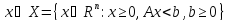
Можно перейти от одной задачи к другой.
Любая ЗЛП сводится к канонической с помощью:
- если в исходной постановке ищется min целевой ф-ии
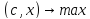 , то–(c,x)превращает исх задачу в задачу о max.
, то–(c,x)превращает исх задачу в задачу о max. - если
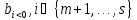 , то соотв ограничения умножаем на (-1), чтобы превратить правую часть в положительную.
, то соотв ограничения умножаем на (-1), чтобы превратить правую часть в положительную. - если m ¹ 0, т.е. в исх постановке присутствуют огранич нер-ва то вводятся
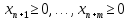 и ограничение нер-ва приводят к виду
и ограничение нер-ва приводят к виду
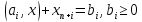 и
и 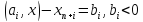
переменные  назыв свободными, они характеризуют величину неиспользованного ресурса.
назыв свободными, они характеризуют величину неиспользованного ресурса.
- если на некот переменную не наложено ограничение на знак, то делают замену
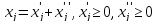 c соотв изменением целевой ф-и, если
c соотв изменением целевой ф-и, если 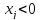 то замена
то замена 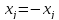
- в некот задачах м присутствовать двусторонние прямые ограничения
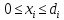 , тогда правое нер-во относится к основным ограничениям и применяют 3)
, тогда правое нер-во относится к основным ограничениям и применяют 3) - двусторонние прямые огранич вида
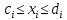 сводятся к
сводятся к 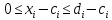 или
или 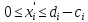 соотв изменениями в целевой ф-и
соотв изменениями в целевой ф-и
Рассм задачу ЛП внорм форме: 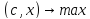

Если множество планов выпуклое, тогда решение сущ., то найдется хотя бы 1 угл.т. мн-ва в которой это решение достигается.
УГЛОВОЙ ТОЧКОЙ мн-ва 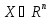 наз. точка x Î X, кот не может быть представлена как точка отрезка
наз. точка x Î X, кот не может быть представлена как точка отрезка
|
|
|
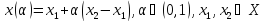
для любых произв т. 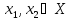
Критерий угловой точки множества.
Рассмотрим задачу в канонической форме: 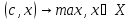 (1),
(1),  (2).
(2).
Теор(Критерий угловой точки):Обозначим ч/з  столбцы матр.А, тогда основные ограничения в системе (2) можно записать в виде:
столбцы матр.А, тогда основные ограничения в системе (2) можно записать в виде:  . Предположим, что матр.А в системе (2) имеет
. Предположим, что матр.А в системе (2) имеет 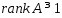 , т.е. матр.А ненулевая.Для того, чтобы точка
, т.е. матр.А ненулевая.Для того, чтобы точка 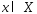 была угловой точкой –G необходимо и достаточно, чтобы сущ.
была угловой точкой –G необходимо и достаточно, чтобы сущ. 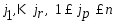 , что справедливо рав-во:(3)
, что справедливо рав-во:(3) 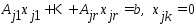 , если
, если 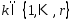 и
и  – ЛНЗ.
– ЛНЗ.
Док-во: Необходимость:Пусть 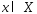 – угловая точка этого мн-ва.а)
– угловая точка этого мн-ва.а) 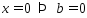 . Т.к. матр. А в соотношении (2) невырождена, то сущ.r ЛНЗ векторов
. Т.к. матр. А в соотношении (2) невырождена, то сущ.r ЛНЗ векторов 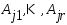 , то выполнено
, то выполнено 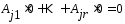 . т.е. (3) справедливо;
. т.е. (3) справедливо;
б) 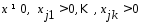 тогда основные ограничения в (2) превратятся в равенство:
тогда основные ограничения в (2) превратятся в равенство: 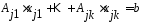 (4). Рассм. Рав-во
(4). Рассм. Рав-во 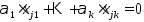 (5). Построим точки
(5). Построим точки 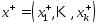 и
и 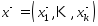 след. обр.:
след. обр.:
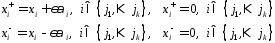
т.к. 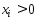 ,то
,то  к рав-ву (4) прибавим и отнимем рав-во (5) умноженное на
к рав-ву (4) прибавим и отнимем рав-во (5) умноженное на 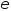 получим что выполняются рав-ва:
получим что выполняются рав-ва:
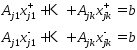 , т.е
, т.е 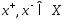 . Легко видеть
. Легко видеть 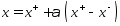 , но х – угловая точка след-но
, но х – угловая точка след-но 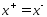 след-но
след-но 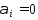 в (5),т.е.вектора
в (5),т.е.вектора 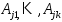 – ЛНЗ след-но
– ЛНЗ след-но 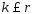
Если 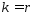 , то (3) – доказано, если
, то (3) – доказано, если 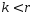 , то к векторам
, то к векторам 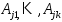 можно добавить вектора
можно добавить вектора 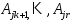 так, чтобы
так, чтобы 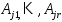 – ЛНЗ, тогда (3) примет вид:
– ЛНЗ, тогда (3) примет вид: 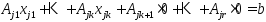 .
.
Достаточность: пусть для точки 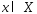 справедливо (3):
справедливо (3): 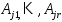 – ЛНЗ, где
– ЛНЗ, где 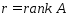 . Предположим, что
. Предположим, что 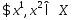 , что
, что 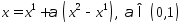 (6). Покажем, что (6) возможно только при
(6). Покажем, что (6) возможно только при 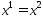 . Рассмотрим нулевую координату точки х:
. Рассмотрим нулевую координату точки х: 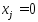 , т.е.
, т.е. 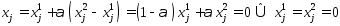 . Докажем (6) для тех координат, которые больше 0. Положительными коор-ами т. х могут быть только те, у которых индекс
. Докажем (6) для тех координат, которые больше 0. Положительными коор-ами т. х могут быть только те, у которых индекс 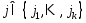 . Пусть
. Пусть 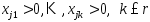 Сл. когда
Сл. когда 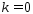 или
или 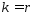 не исключается, тогда система осн-х огр-ий из (2) преобразуется к виду:
не исключается, тогда система осн-х огр-ий из (2) преобразуется к виду: 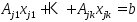 . Докажем, что
. Докажем, что 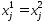 , если
, если 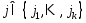 . Точки
. Точки 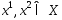 было доказано, что
было доказано, что 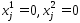 , когда
, когда 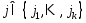 след-но
след-но 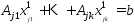 и
и 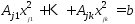 . Вектора
. Вектора 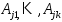 – ЛНЗ, а разложение произвольного вектора пр-ва по ЛНЗ-векторам явл. единственным, след-но
– ЛНЗ, а разложение произвольного вектора пр-ва по ЛНЗ-векторам явл. единственным, след-но 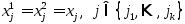 для строго пол-ых координат.
для строго пол-ых координат.
Дата добавления: 2019-07-15; просмотров: 187; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
