Обоснование и алгоритм метода ломаных решения задачи одномерной минимизации.

⇐ ПредыдущаяСтр 2 из 6Следующая ⇒

Метод ломаных применяется для решения задачи (1), без требования унимодальности ф-ции f, но эти ф-ии должны уд. усл. Липшица.

Опр. Говорят, что ф-ция 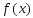уд.усл. Липшица на [a;b], если 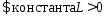, что 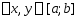. (2) Геометрическое усл.Липшица означает, что угловой коэф-т 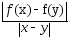хорд, кот соединяют две произвольные точки графика ф-цийy=f(x) не превосходит константы L.

Если ф-я уд.усл. Липшица на [a;b] то она явл-ся непрерывной на [a;b].

Т1: Пусть f(x)-определена и непрерывна на [a;b] и на каждом [ai;ai+1], где а=a₁<a₂<…<a_n<a_n+1=b уд. усл. Липшица с конст Li, тогда f(x)уд. усл Лип на всем отр-ке [a;b]с конст L=maxLi.

Д-во: выберем произвольные x,y из отрезка [a,b]. Предположим, что т-ка .

Рассм.модуль разности

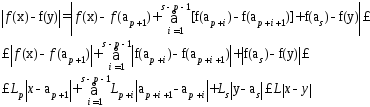
Т2: Пусть f(x)–дифер на [a;b] и её производная огр-на на [a;b], тогда эта ф-ция уд. усл. Лип с конст. L=sup|f’(x)|

Д-во: т.к. ф-ция f(x) диф-ма, то по формуле конечных приращений приращение ф-ции

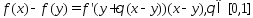
Отсюда и из ограниченности производной следует утв. теоремы.

Пусть ф-я f(x) удовлетворяет на [a;b] условию Липш (2) с константой L. Зафиксируем некоторую точку y из [a;b] и построим ф-цию

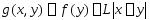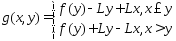g(y,y)=f(y)

. Ф-ция g явл. кусочно-линейной ф-цией, ее график есть ломаная с углами наклона L (до y) и –L (после y) и в т-ке y g(y,y)=f(y).

Рассмотрим нерав-во 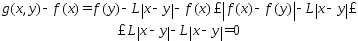т.е. , .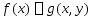

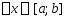Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных

Выбирем некот т-ку 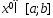. Построим ф-ю

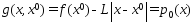и определим из усл. 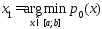. Очевидно, чтоx¹=a или x¹=b. Пусть в результате выполнения нескольких шагов определены т-ки х¹,х²,…,хⁿ, n 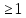. Построим ф-цию g(x,xⁿ)=f(xⁿ)-L|x- xⁿ |.

Строим ф-цию

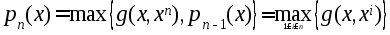Следующее приближение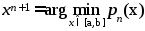

Процесс вычисл. продолж. до тех пор, пока не будет выполнено нерав-во 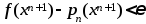, где 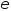- заданная точность. В кач-ве решения задачи выбирается т-ка .

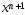Зам.Метод ломаных сходится при любом начальном при любом начальном приближении.

Зам . Для всех х 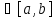справедливо соотнош.

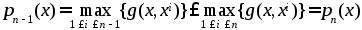
т.е. ф-ции р_n(х) приближают ф-цию f(x) снизу, оставаясь каждый раз не выше графика ф-ции f(x).

Зам, Недостаток – с ростом числа шагов растет требуемый объем памяти вычисл машины.

Зам. Для применения метода надо знать константу Липшица.

Теорема. Пусть ф-я 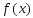уд. усл. Липшица на [a;b], тогда посл-ть 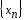полученная методом ломанных такая, что:

1) 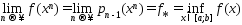(1), причем 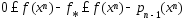(2)

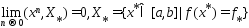2) (3)

Док-во. Рассмотрим 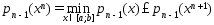(4)

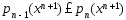(5), 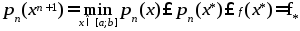(6) , где 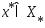. Из (4)-(6) получаем

т.е. послед-ность 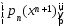явл. возрастающей и ограничена сверху, поэтому 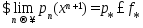. Кроме того, из (4)-(6) следует оценка (2). Покажем, что 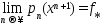. Т.к. 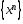ограничена, то из нее можно выделить сходящуюся подпослед-ность 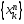. Пусть 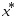- некотор. т-ка послед-ности 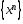. Послед-ность 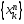сходится к т-ке 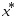при 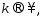n¹<n²<…<n^k<…

Пример. f(x)=|x²-1|, x 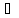[-2,3]. На отр. [-2,3] ф-ция уд. усл. Липшица с константойL₁=4, на отр. [-1,1] L₂=2, на отр. [1,2] L₃=6. На всем отр. L=6. Строим ф-цию g(x,0)=1-6|x|. При x<0, g(x,0)=1+6x, g(-1,0)=-5, x>0, g(x,0)=1-6x, g(1,0)=-5. Т-ка x¹. g(x,3)=8-6|x-3|, g(x,3)=8+6x-18.

Следующ. т-ка x² определ. как min g(x,-2)=3-6|x+2|, g(x,-2)=3-6x-12

Обоснование сходимости метода ломаных решения задачи одномерной минимизации.

Сходимость и оценка погрешности метода Метод ломаных сходится, что утверждается в следующей теореме. Теорема. Пусть J (u) - произвольная функция, удовлетворяющая на [a, b] условию (4). Тогда последовательность {un}, полученная с помощью метода ломаных, такова, что: 1) ( ) ( ) [ ] J u p u J J (u) u a b n n n n n , 1 lim lim * inf Î + ®¥ ®¥ = = = , причем справедлива оценка 0 ( ) * ( ) ( ), 0,1, ... £ J un+1 - J £ J un+1 - pn un+1 n = ; (5) 2) {un}сходится к множеству U * точек минимума J (u) на [a, b], т.е. limr( , *) = 0 ®¥ un U n . Оценка константы Липшица Для применения метода ломаных необходимо знать константу Липшица функции J (u). Для её оценки можно воспользоваться следующим алгоритмом. Разобьем отрезок [a,b] на m подотрезков: a = v < v < ... < vm £ b 0 1 . Обозначим ( ) ( ) 1 1 1, max - - = - - = i i i i i m m u u J u J u L . Несложно доказать, что для последовательности Lm справедливы следующие утверждения: , 1, 2, .... Lm £ Lm+1 £ L m = ; Lm L m = ®¥ lim . Следовательно, при достаточно большом m в качестве приближенного значения константы Липшица можно взять величину Lm . Примечание. Заниженная оценка константы Липшица может привести к неправильному нахождению минимального значения и точки минимума функции.

Дата добавления: 2019-07-15; просмотров: 588; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!