ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ В ПРОСТЫХ РАМАХ
Рама – это стержневая система (рис. 2.1, а), у которой все или некоторые из узловых соединений являются жесткими. Жесткий узел характеризуется тем, что при деформировании стержневой системы угол сопряжения стержней не изменяется (рис. 2.1, б). Горизонтальные стержни называются ригелями , а вертикальные стержни - стойками.
| Рис. 2.1 Рама |
| ригель |
| жесткий узел |
| стойка |
| а) |
| б) |
| стойка |
| α |
| β |
| P |
| α |
| β |
| α |
| β |
| 1 |
| 2 |
| 3 |
| 4 |
| т. н. |
При нагружении рамы в ее плоскости в поперечных сечениях стержней возникают внутренние усилия: поперечная сила Q, изгибающий момент М и продольная сила N. Определение внутренних усилий в стержнях рамы выполняется с помощью метода сечений.
Для построения эпюр М, Q и N в рамах используются правила построения эпюр для балок.
При построении эпюр внутренних усилий придерживаются следующих правил:
1) ось стержня принимается за ось абсцисс:
2) вычисленные ординаты эпюр откладываются перпендикулярно к продольной оси стержней;
3) положительные ординаты эпюры Q откладываются вверх от оси ригеля и влево от оси стойки;
4) ординаты эпюры М откладываются со стороны растянутых волокон элементов рамы;
5) ординаты эпюры N откладываются, как правило, симметрично по обе стороны от оси рассматриваемого стержня. Знак на эпюре N обязателен;
6) штриховка на эпюре производится перпендикулярно к оси соответствующего стержня.
|
|
|
Проверка правильности построения эпюр M, Q и N включает в себя статическую проверку, которая заключается в проверке равновесия любой отсеченной части под действием внешней нагрузки и усилий M, Q и N, заменяющих действие отсеченных частей рамы.
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
МЕТОДОМ СИЛ
В статически неопределимых стержневых системах число неизвестных опорных реакций и внутренних усилий превышает число независимых уравнений равновесия, которые можно составить для их определения. Разность между ними характеризует степень статической неопределимости системы n, которая равна числу избыточных («лишних») связей.
Степень статической неопределимости стержневых систем определяется по формуле Чебышева П.Л. n = 3K + Cо- 3 - Ш, где K - число замкнутых контуров, Cо - число опорных стержней, 3 - число линейно-независимых уравнений статики для плоской задачи, Ш - число простых одиночных шарниров.
Наличие промежуточного шарнира, Простой шарнир, соединяющий два стержня, понижает степень статической неопределимости на единицу.
При n > 1 система является статически неопределимой, при n = 0 она статически определима, а при n < 0 представляет собой геометрически изменяемую систему или механизм.
|
|
|
На рис. 3.1 показаны статически неопределимые рамы.
| Рис. 3.1 Статически неопределимые рамы |
| n = 3×0 + (3+2+1) - 3 - 1 = 2 |
| ш = 1 |
| k = 1 |
| ш = 1 |
| Cо = 3 |
| Cо = 2 |
| Cо = 1 |
| Cо = 2 |
| Cо = 1 |
| n = 3×1 + (2+1) - 3 - 1 = 2 |
Одним из основных методов расчета статически неопределимых стержневых систем является метод сил.
Порядок расчета статически неопределимых систем по методу сил.
| X1 |
| а) |
| б) |
| X2 |
| е) |
| Рис. 3.2 Расчет статически неопределимой системы |
| P |
| в) |
| P |
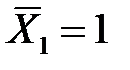
|
| г) |
| д) |
| Mp |
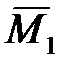
|
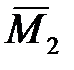
|
| P |
| ОС |
| ж) |
| ЭС |
| M |
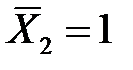
|
n = 3K + Cо- 3 - Ш=
= 3×0 + (1+1+3) - 3 - 0 = 2.
2. Выбираем основную систему (ОС) (рис.3.2, б), которая получается из заданной системы путем удаления лишних связей. Основная система должна быть определимой и геометрически неизменяемой.
3. Образуем эквивалентную систему (ЭС) путем нагружения основной системы заданной нагрузкой "P" и неизвестными усилиями Х1 и Х2, заменяющими действие отброшенных связей (рис.3.2, в).
4. Составляем канонические уравнения метода сил, которые выражают условия эквивалентности основной и заданной систем. Число уравнений должно равняться степени статической неопределимости.
|
|
|
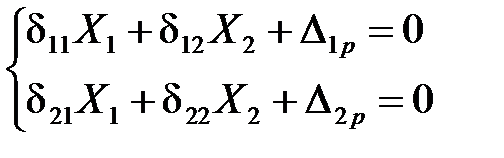
Коэффициенты системы dij представляют собой перемещения по направлению усилий Х i от действия единичных сил 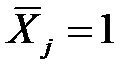 в основной системе. Коэффициенты d11, d22 называются главными коэффициентами. Они всегда положительны. Коэффициенты dij (i ¹ j) называются побочными коэффициентами. Для них на основании теоремы Максвелла о взаимности перемещений справедливо равенство dij = dji. Величины Di р называются свободными (грузовыми) членами и равны перемещениям в основной системе по направлению усилий Х i от действия заданной нагрузки "Р".
в основной системе. Коэффициенты d11, d22 называются главными коэффициентами. Они всегда положительны. Коэффициенты dij (i ¹ j) называются побочными коэффициентами. Для них на основании теоремы Максвелла о взаимности перемещений справедливо равенство dij = dji. Величины Di р называются свободными (грузовыми) членами и равны перемещениям в основной системе по направлению усилий Х i от действия заданной нагрузки "Р".
5. Строим в основной системе эпюру изгибающих моментов M р от заданной нагрузки (рис.3.2, г).
6. Строим в основной системе эпюру изгибающих моментов  и
и 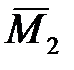 от действия единичных сил
от действия единичных сил  и
и  (рис.3.2, д, е).
(рис.3.2, д, е).
7. Определяем коэффициенты dij и свободные члены Di р канонических уравнений метода сил, используя формулы Верещагина, трапеций, Симпсона.
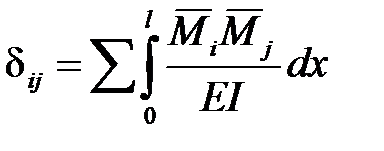 ,
,
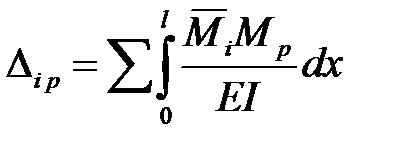 .
.
8. Решаем систему канонических уравнений и находим значения неизвестных усилий Х1 и Х2.
9. Проверяем правильность решения системы канонических уравнений, подставляя найденный усилия Х1 и Х2 в канонические уравнения.
|
|
|
10. Строим окончательную эпюру изгибающих моментов M (рис.3.2, ж), используя принцип независимости действия сил по формуле
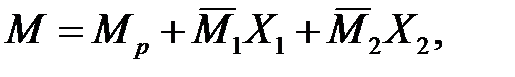
для каждого сечения.
11. Выполняем деформационную проверку правильности построения окончательной эпюры изгибающих моментов M, используя интеграл Мора для определения обобщенных перемещени й в направлениях удаленных связей:

Относительная погрешность для этих условий не должна превышать 3%.
| X2 |
| а) |
| в) |
| X1 |
| Рис. 3.3 Выбор и расчет рациональной основной системы |
| X1 |
| P |
| г) |
| д) |
| е) |
| 1 |
| 1 |
| Mp |
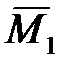
|
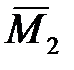
|
| ОС |
| ЭС |
| б) |
| P |
| M |
| ж) |
| P |
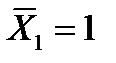
|
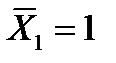
|
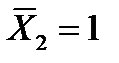
|
13. Выполняем статическую проверку расчета. Проверяем равновесие отсеченных частей и узлов стержневой системы под действием заданной нагрузки и усилий M, Q и N, заменяющих действие отсеченных частей системы. Относительная погрешность не должна превышать 3%.
Для неразрезной балки рациональной основной системы является система, полученная из заданной путем введения врезных шарниров над промежуточными опорами и в заделки.
При выборе для балки рациональной основной системы порядок расчета приведен на рис.3.3.
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Сочетание двух и более простых видов деформаций называется сложным сопротивлением.
При расчетах на сложное сопротивление используют принцип независимости действия сил. В общем случае под действием внешних сил в сечениях бруса возникают шесть внутренних силовых факторов N, Q Y, Q Z, М Y, М Z, М K.
Суммарные нормальные напряжения, действующие в сечении, суммируются алгебраически:
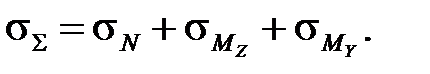 (4.1)
(4.1)
4.1 КОСОЙ ИЗГИБ
Косым изгибом называется вид изгиба, при котором плоскость действия изгибающего момента в поперечном сечении бруса не совпадает ни с одной из главных плоскостей бруса.
При косом изгибе в произвольном сечении балки возникает четыре внутренних силовых фактора: изгибающие моменты MY и MZ и поперечные силы QY и QZ. Влияние поперечных сил в большинстве случаев не учитывается.
Косой изгиб можно рассматривать как сочетание двух прямых изгибов, вызванных изгибающими моментами MY и MZ относительно главных центральных осей инерции поперечного сечения Y и Z.
На основании принципа независимости действия сил все внешние силы раскладывают на составляющие, действующие в двух главных плоскостях балки XOZ и XOY, и строят эпюры изгибающих моментов MY и MZ .
Результирующие нормальные напряжения в сечении в точке B (y, z) определяются на основе принципа независимости действия сил алгебраическим сложением:
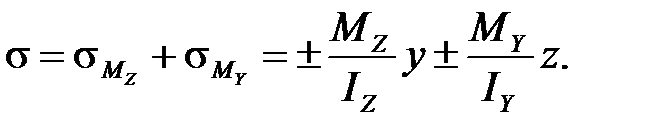 (4.2)
(4.2)
Все величины, входящие в формулу, подставляются по абсолютному значению, а знаки перед слагаемыми определяются из физических соображений (рис. 4.1). Если изгибающий момент М Y или М Z вызывает в точке растягивающее напряжение, то перед слагаемым должен быть знак плюс, если вызывает сжимающее напряжение - знак минус.
| PY |
| Z |
| Y |
| PZ |
| X |
| z |
| y |
| B |
| Y |
| Z |
| MZ |
| MY |
| Рис. 4.1 Косой изгиб |
| P |
| b > 0 |
| n |
| n |
Нейтральная линия – это геометрическое место точек, в которых нормальные напряжения равны нулю.
Уравнение нейтральной линии n - n (рис. 4.1) при косом изгибе запишем для т. В, находящейся в I четверти системы координат:
 (4.3)
(4.3)
Это уравнение прямой, проходящей через центр тяжести сечения под углом β к оси Z где yО, zО - координаты точек, лежащих на нейтральной линии.
Положительный угол β отсчитывается от положительного направления оси Z по ходу часовой стрелки и
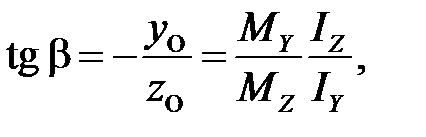 (4.4)
(4.4)
| Y |
| Z |
| MZ |
| MY |
| Рис. 4.2 Нейтральная линия и эпюра sсум при косом изгибе |
| b > 0 |
| n |
| n |
| о |
| о |
| A |
| B |
| sA |
| sB |
| эп. sсум |
Нейтральная линия проходит через те четверти системы координат, в которых изгибающие моменты М Y и М Z вызывают нормальные напряжения разных знаков. Моменты М Y и М Z в формулу (4.4) подставляют с учетом знаков нормальных напряжений, которые они вызывают в I четверти.
Опасными точками в сечении являются те, которые наиболее удалены от нейтральной линии n - n: точки А и В.
Для построения плоской эпюры суммарных нормальных напряжений из точек А и В проводим линии параллельные нейтральной линии и перпендикулярно им базисную линию о-о и строим эпюру суммарных напряжений эп. sсум.
Для пластичных материалов условие прочности запишем для наиболее удаленной точки от нейтральной линии:
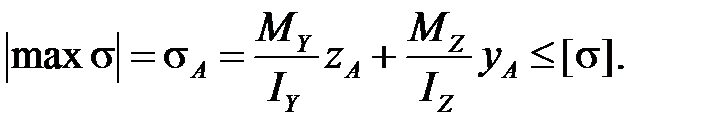
Для хрупких материалов условие прочности записывается для двух опасных точек в растянутой и сжатой зонах:
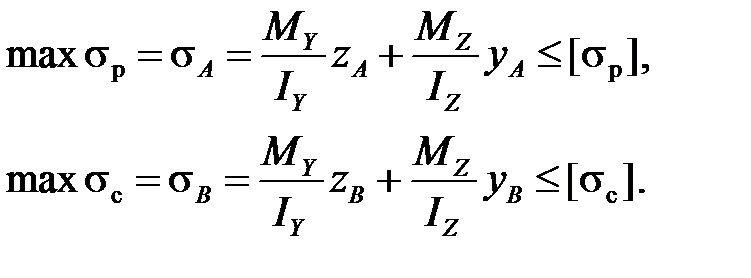
| Y |
| Z |
| Рис. 4.3 Определение перемещений |
| f |
| fZ |
| fY |
| n |
| n |
 и
и 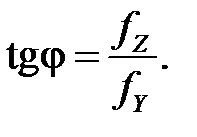
4.2 ИЗГИБ С РАСТЯЖЕНИЕМ (СЖАТИЕМ).
ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ (СЖАТИЕ)
| Y |
| Z |
| MZ |
| MY |
| B |
| X |
| N |
| z |
| y |
| Рис. 4.4 Изгиб с растяжением (сжатием) |
На основании принципа независимости действия сил суммарное нормальное напряжение в поперечных сечениях равно:
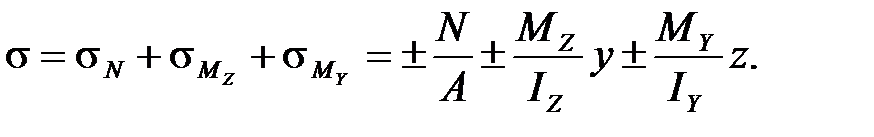 (4.5)
(4.5)
| Y |
| Z |
| MZ |
| MY |
| n |
| n |
| о |
| о |
| A |
| B |
| sA |
| sB |
| эп. sсум |
| N |
| Рис. 4.5 Нейтральная линия при изгибе с растяжением (сжатием) |
| aY |
| aZ |
Уравнение нейтральной линии n - n (4.6) при изгибе с растяжением (сжатием) - это уравнение прямой, не проходящей через центр тяжести сечения и отсекающей по осям координат отрезки aY и aZ (рис. 4.5):
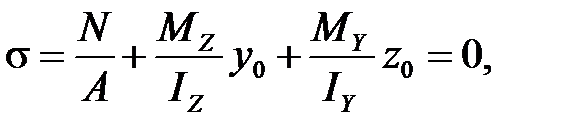 (4.6)
(4.6)
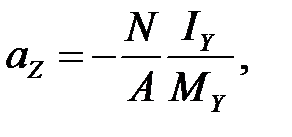 (4.7)
(4.7)
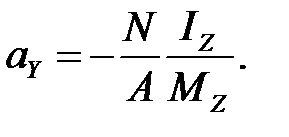 (4.8)
(4.8)
Моменты М Y , М Z и продольная сила N подставляются в формулы (4.7) и (4.8) с учетом знаков нормальных напряжений, которые они вызывают в I четверти.
Опасными точками в сечении являются те, которые наиболее удалены от нейтральной линии: точки A и B.
Для построения плоской эпюры суммарных нормальных напряжений из точек А и В проводим линии параллельные нейтральной линии и перпендикулярно им базисную линию о-о и строим эпюру суммарных нормальных напряжений (эп. sсум).
Для пластичных материалов условие прочности записывается для наиболее опасной точки:
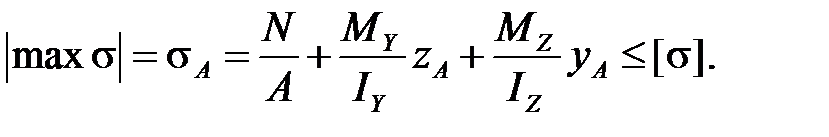
Для хрупких материалов условие прочности записывается для двух опасных точек наиболее удаленных от нейтральной линии: в растянутой зоне - точке А и в сжатой зоне - точке В.
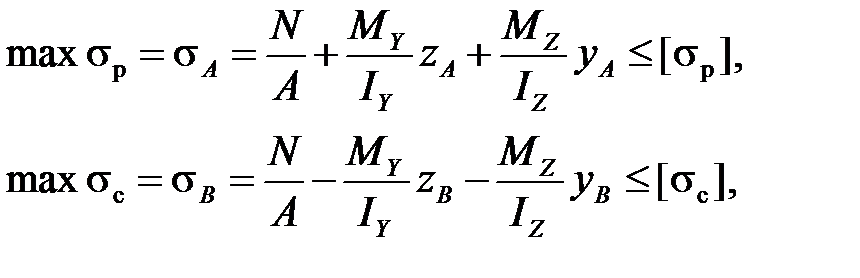
где индекс "р" - означает растяжение, "с" - сжатие.
Внецентренным растяжением (сжатием) называется вид деформации (рис. 4.6, а), при котором внешняя сила P параллельна оси стержня, но приложена внецентренно в точке В.
| Y |
| Z |
| P |
| yP |
| zP |
| B |
| Y |
| Z |
| N |
| MZ |
| MY |
| Рис. 4.6 Внецентренное растяжение (сжатие) |
| а) |
| б) |
Точку B приложения силы Р называют центромдавления или полюсом.
Координаты zP и yP точки B приложения силы Р называются эксцентриситетами.
При внецентренном действии продольной силы Р в поперечных сечениях возникают три внутренних силовых фактора (рис. 4.6, б). Внутренние усилия равны: N = P, MZ = PyP, MY = PzP и, следовательно, все сечения стержня равноопасны.
Нормальные напряжения при внецентренном растяжении (сжатии) определяются по формуле:
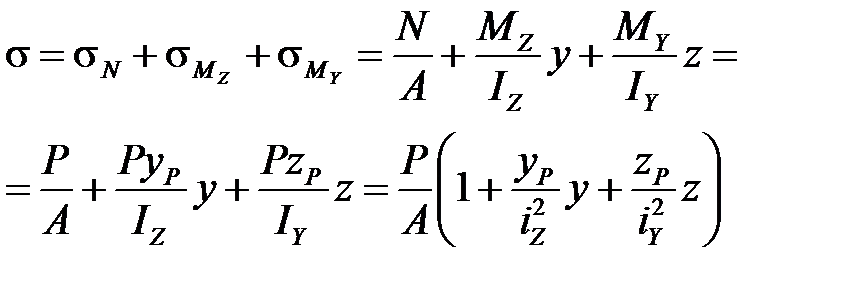 (4.9)
(4.9)
где  ─ радиус инерции относительно оси Z,
─ радиус инерции относительно оси Z,  ─ радиус инерции относительно оси Y.
─ радиус инерции относительно оси Y.
Уравнение нейтральной линии при внецентренном растяжении (сжатии):
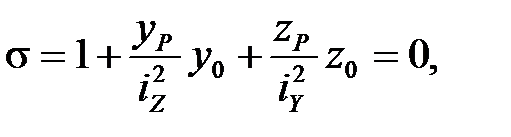 (4.10)
(4.10)
где y0, z0 - координаты точек, лежащих на нейтральной линии.
Нейтральная линия отсекает отрезки по осям -
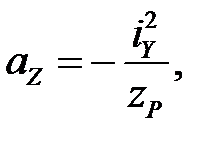 (4.11)
(4.11)
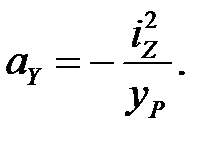 (4.12)
(4.12)
При внецентренном растяжении (сжатии) нейтральная линия может как пересекать сечение, так и находиться за его пределами.
4.3 ИЗГИБ С КРУЧЕНИЕМ ВАЛОВ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Вид сложного сопротивления, когда в поперечных сечениях стержня (вала) возникают изгибающий и крутящий моменты, называется изгибом с кручением (рис. 4.7).
| Z |
| MZ |
| MY |
| Y |
| X |
| M К |
| Рис. 4.7 Изгиб с кручением |
При определении нормальных напряжений при круглом сечении используем суммарный изгибающий момент MИ для определения максимальных нормальных напряжений:
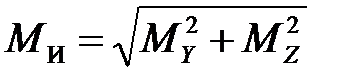 и
и 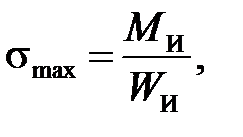 гдe WИ - осевой момент сопротивления для круглого сечения и
гдe WИ - осевой момент сопротивления для круглого сечения и 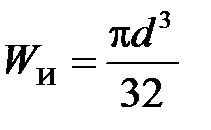 - для сплошного сечения,
- для сплошного сечения, 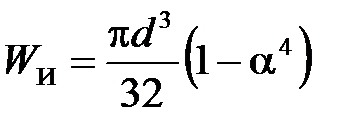 - для кольцевого сечения.
- для кольцевого сечения.
Для отыскания опасной точки вала диаметром d необходимо построить эпюры изгибающих моментов М Z от действия вертикальных сил, М Y от горизонтальных сил, и крутящих моментов М K.
При совместном действии нормальных и касательных напряжений имеем плоское напряженное состояние и для проверки прочности необходимо применить одну из теорий прочности.
Условие прочности для валов из пластичных материалов по третьей или четвертой теориям прочности имеет вид:
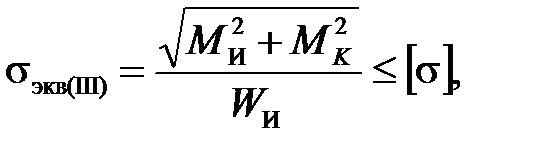
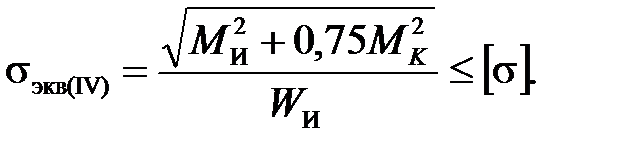
Условие прочности валов из хрупких материалов по теории прочности Мора имеет вид:

где 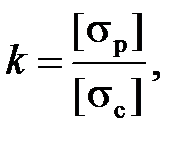 и [sр] и [sс] допускаемые напряжения при одноосном растяжении (сжатии).
и [sр] и [sс] допускаемые напряжения при одноосном растяжении (сжатии).
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Устойчивость - способность стержня сохранять первоначальную форму равновесия в нагруженном состоянии и восстанавливать ее после снятия нагрузки
Потеря устойчивости прямолинейной формы равновесия центрально сжатого стержня называется продольным изгибом.
Критической силой Pкр называются наименьшее значение центрально приложенной сжимающей силы, при которых первоначальная форма равновесия стержня становится неустойчивой.
Для обеспечения устойчивости должно выполняться условие устойчивости для сжимающей силы P
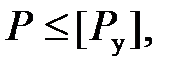 (5.1)
(5.1)
где [Pу] = Pкр /ny. Здесь ny - коэффициент запаса на устойчивость, [Pу] - допускаемая сжимающая сила при расчете на устойчивость.
При работе материала в пределах упругости, когда нормальные напряжения s стержня не превышают предела пропорциональности sпц
sкр ≤ sпц , (5.2)
| P |
| P |
| P |
| P |
| m =1 |
| m =0,7 |
| m =0,5 |
| m =2 |
| Рис. 5.1 Способы закрепления сжатых стержней |
| l0 = 0,5 l |
| 0,25 l |
| 0,25 l |
| l0 = 0,7 l |
| l0 = l |
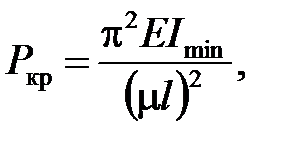 (5.3)
(5.3)
где E - модуль упругости, Imin - минимальный осевой момент инерции поперечного сечения, l0 = m l - приведенная длина стержня, m - коэффициент приведения длины, определяемый способом закрепления стержня (рис. 5.1).
Формула Эйлера может быть записана в виде
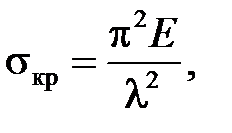 (5.4)
(5.4)
где 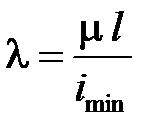 - гибкость стержня,
- гибкость стержня, 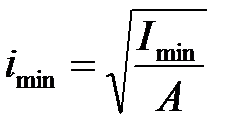 - минимальный главный радиус инерции, А - площадь поперечного сечения стержня.
- минимальный главный радиус инерции, А - площадь поперечного сечения стержня.
Из условия 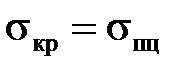 получим предельное значение гибкости lпред:
получим предельное значение гибкости lпред:
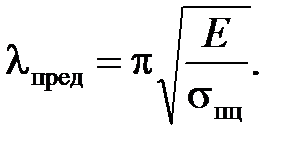 (5.5)
(5.5)
Таким образом, если гибкость стержня  можно тспользовать формулу Эйлера. Для стали Ст. 3 lпред = 100.
можно тспользовать формулу Эйлера. Для стали Ст. 3 lпред = 100.
Для сжатых стержней, работающих за пределом упругости (sкр ≥ sпц или 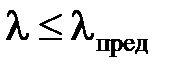 ) применяется формула Ясинского:
) применяется формула Ясинского:
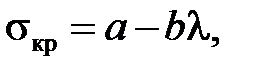 (5.6)
(5.6)
где a и b - коэффициенты, определяемые опытным путем.
Для стали Ст.3 a = 310 МПа, b = 1,14 МПа.
Для дерева (сосна, ель) a = 40 МПа, b = 0,203 МПа.
Для чугуна формула Ясинского имеет вид:
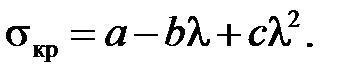 (5.7)
(5.7)
где a = 776 МПа, b = 12 МПа, с = 0,053 МПа.
Формула Ясинского применима для стержней из малоуглеродистой стали Ст.3 при гибкости l = 40 ¸ 100. При гибкости l = 0 ¸ 40 напряжение s кр считается постоянным и равным пределу текучести s т .
В расчетах на устойчивость используется практическая формула
[P] = j[sс]A, (5.8)
где [P] - допускаемая сила, которую можно приложить к стержню без потери его устойчивости, j - коэффициент уменьшения допускаемого напряжения для сжатых стержней (коэффициент продольного изгиба), [sс] - допускаемое напряжение на центральное сжатие, А - площадь поперечного сечения стержня.
| j |
| j1 |
| j2 |
| jλ |
| l |
| l |
| l1 |
| l2 |
| Рис. 5.2 Метод линейной интерполяции |
Тогда 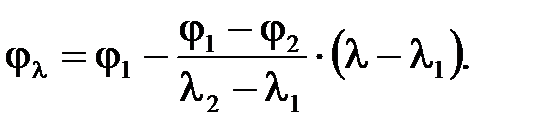
|
Таблица 5.1 Коэффициенты j | ||||
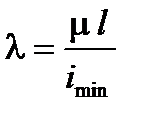
| Ст2, Ст3 | Ст5 | Чугун | Дерево |
| 0 | 1,00 | 1,00 | 1,00 | 1,00 |
| 10 | 0,99 | 0,98 | 0,97 | 0,99 |
| 20 | 0,96 | 0,95 | 0,91 | 0,97 |
| 30 | 0,94 | 0,92 | 0,81 | 0,93 |
| 40 | 0,92 | 0,89 | 0,69 | 0,87 |
| 50 | 0,89 | 0,86 | 0,57 | 0,80 |
| 60 | 0,86 | 0,82 | 0,44 | 0,71 |
| 70 | 0,81 | 0,76 | 0,34 | 0,60 |
| 80 | 0,75 | 0,70 | 0,26 | 0,48 |
| 90 | 0,69 | 0,62 | 0,20 | 0,38 |
| 100 | 0,60 | 0,51 | 0,16 | 0,31 |
| 110 | 0,52 | 0,43 | - | 0,25 |
| 120 | 0,45 | 0.36 | - | 0,22 |
| 130 | 0,40 | 0,33 | - | 0,18 |
| 140 | 0,36 | 0,29 | - | 0,16 |
| 150 | 0,32 | 0,26 | - | 0,14 |
| 160 | 0,29 | 0,24 | - | 0,12 |
| 170 | 0,26 | 0,21 | - | 0,11 |
| 180 | 0,23 | 0,19 | - | 0,10 |
| 190 | 0,21 | 0,17 | - | 0,09 |
| 200 | 0,19 | 0,16 | - | 0,08 |
Коэффициент запаса на устойчивость определяется по формуле:
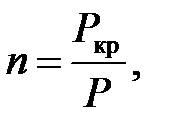 (5.9)
(5.9)
где P - приложенная сжимающая сила.
При подборе сечения стержня, работающего на устойчивость, используется практическая формула и метод последовательных приближений (итераций).
Первое приближение:
1) Принимаем j1 = 0,5;
2) Определяем площадь и размеры сечения - 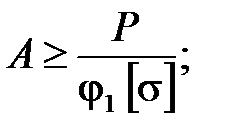
3) Определяем минимальный момент инерции Imin и минимальный радиус инерции сечения - 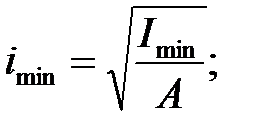
4) Определяем гибкость стержня - 
5) Определяем коэффициент j2 для рассчитанной гибкости λ, используя таблицу 5.1 и метод линейной интерполяции;
6) Если j2 отличается от j1 более чем на ± 5%, то расчет снова повторяют с п.2, приняв новое j1 равным половине суммы прежнего значения j1 и значения коэффициента j2 -
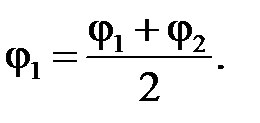
7) Проверяем выполнение условий устойчивости

сравнивая расчетное напряжение sрасч с допускаемым напряжением для материала.
РАСЧЕТ НА УДАР
Динамическая нагрузка характеризуется быстрым изменением во времени своего значения и вызывает в элементах конструкции значительные силы инерции. При расчетах используют пр инцип Д’Аламбера: «Любой элемент конструкции при динамической нагрузке находится в равновесии под действием внешних сил и сил инерции».
Ударная нагрузка прикладывается за очень малый промежуток времени и является опасной для конструкции. Время удара исчисляется сотыми долями секунды. В технической теории удара предполагается:
1) выполняется закон сохранения энергии - энергия ударяющего тела полностью переходит в энергию упругой деформации системы;
2) выполняется закон Гука, т.е. перемещения системы при ударе подобны перемещениям при статическом приложении груза;
3) ударяющее тело с момента соприкосновения с ударяемым движутся как единое целое, т.е удар является неупругим.
| Q |
| h |
| Рис. 6.1 Вертикальный удар |
| Dст(Q) |
| Dдин |
При вертикальном ударе без учета массы ударяемой системы (рис. 6.1) динамический коэффициент kД равен:
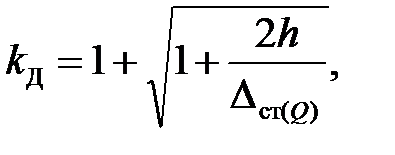 (6.1)
(6.1)
или
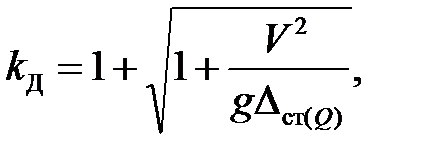 (6.2)
(6.2)
где h - высота падения груза весом Q, Dст(Q) - прогиб в точке удара от статически приложенной силы Q в этой же точке, V - скорость груза в момент соударения, g = 9,81 м/c2 - ускорение свободного падения.
Максимальные динамические напряжения и перемещения, возникающие в конструкции при ударе, равны:
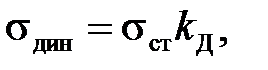 (6.3)
(6.3)
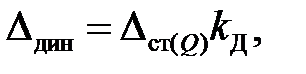 (6.4)
(6.4)
где 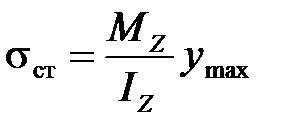 - нормальное напряжение от действия статической силы Q,
- нормальное напряжение от действия статической силы Q,
| Q |
| V |
| Рис. 6.2 Горизонтальный удар |
| Dдин |
Горизонтальный удар.
Динамический коэффициент без учета массы ударяемой системы:
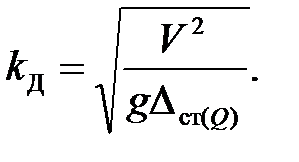 (6.5)
(6.5)
РАСЧЕТ
| Q |
| Ht |
| Рис. 7.1 Вынужденные колебания |
| m |
| Dст(Q) |
| Dполн |
Рассмотрим упругую систему с одной сосредоточенной массой 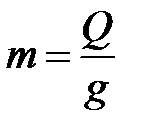 , где Q - вес груза, g = 9,81 м/c2 - ускорение свободного падения. Балка под действием груза Q находится в состоянии статического равновесия, Dст(Q) - статический прогиб от силы Q (рис. 7.1).
, где Q - вес груза, g = 9,81 м/c2 - ускорение свободного падения. Балка под действием груза Q находится в состоянии статического равновесия, Dст(Q) - статический прогиб от силы Q (рис. 7.1).
Система (балка), выведенная из состояния равновесия, совершает собственные колебания с частотой w равной:
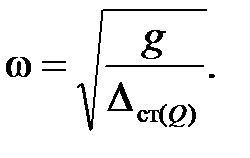 (7.1)
(7.1)
При приложении к массе m внешней гармонической силы Ht = Hsinθt, где q - частота вынуждающей силы, H - амплитуда силы, в системе возникают вынужденные колебания, при этом полное перемещение груза Dполн (рис. 7.1) равно:
Dполн = Dст(Q)+ bDст(H) = kД Dст(Q), (7.2)
где 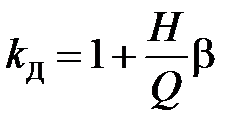 - динамический коэффициент, β - коэффициент нарастания амплитуды колебаний (рис. 7.2),
- динамический коэффициент, β - коэффициент нарастания амплитуды колебаний (рис. 7.2),
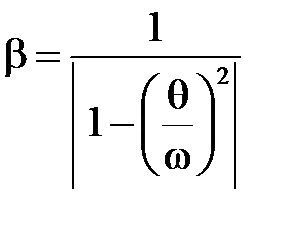 (7.3)
(7.3)
Dст(H) - статический прогиб от силы H.
Рис. 7.2 Кривая зависимости β от 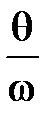
|
| 0 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
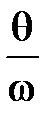
|
| β |
При стремлении q к w происходит нарастание амплитуды колебаний, и при q = w наступает явление резонанса.
При 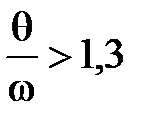 и
и 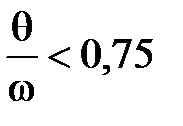 формулу (7.3) можно использовать в расчетах без учета затухания колебаний.
формулу (7.3) можно использовать в расчетах без учета затухания колебаний.
Максимальное динамическое напряжение, возникающее в системе при колебаниях, равно:
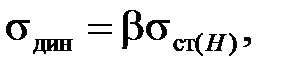 (7.4)
(7.4)
где 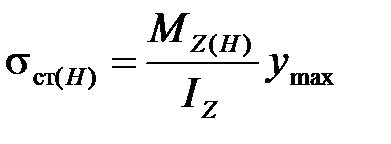 - нормальное напряжение от действия статической силы H, при этом полное напряжение при вынужденных колебаниях равно:
- нормальное напряжение от действия статической силы H, при этом полное напряжение при вынужденных колебаниях равно:
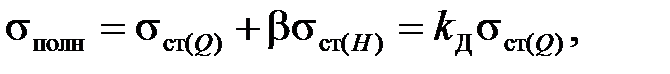 (7.5)
(7.5)
где 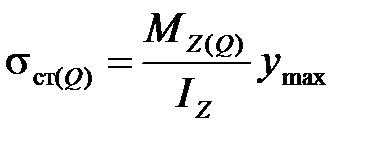 - нормальное напряжение от действия статической силы Q.
- нормальное напряжение от действия статической силы Q.
ЛИТЕРАТУРА
1. Поляков А.А., Кольцов В.М. Сопротивление материалов и основы теории упругости: учебник / А.А. Поляков, В.М. Кольцов Екатеринбург: УГТУ – УПИ, 2008. 458 с.
2. Дарков А.В. Сопротивление материалов / А.В. Дарков, Г.С. Шпиро // М.: Высшая школа, 1989. 624 с.
3. Чупин В.В. Сопротивление материалов. Методические указания по выполнению курсовой работы «Простые виды деформаций. Расчеты на прочность и жесткость стержневых систем». Электронный ресурс: http://study.urfu.ru/Aid/ViewMeta/9550
4. Игнатов Р.Г. Сопротивление материалов: контрольные задания. Часть 2/ Р.Г. Игнатов, Ф.Г.Лялина, А.А. Поляков, Д.Е. Черногубов, В.В. Чупин. Электронный ресурс: http://study.urfu.ru/Aid/ViewMeta/9552
Учебное пособие
СЛОЖНЫЕ ВИДЫ ДЕФОРМАЦИЙ.
Дата добавления: 2019-07-15; просмотров: 594; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
