Обратное интерполирование для равноотстоящих аргументов.
Обратное интерполирование на основе 1ИФН
Задача обратного интерполирования заключается в том, чтобы по функции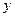 
найти значение аргумента 
.
Предположим, что 
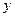монотонна, и значение содержится между 
и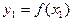 
. Заменяя 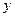интерполяционным полиномом Ньютона, имеем:
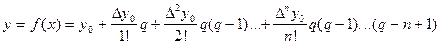
Тогда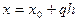 
, где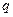 
число шагов, необходимых для достижения точки , исходя из точки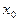 
.
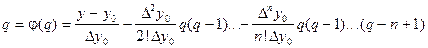
За начальное приближение принимаем:
Применяя метод итераций, получим:
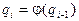
Итерационный процесс, останавливается, когда
и тогда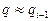 
После этого вычисляется значение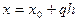
Пример.
Заданы координаты узловых точек. Для значения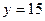 
определить 
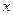с точностью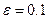 
|
|
|
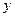
| 4 | 11 |
| 6 | 27 |
| 8 | 50 |
| 10 | 83 |
Решение. Построим горизонтальную таблицу разностей:
| x | y | 
| 
| 
|
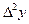
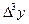
| 4 | 11 | 16 | 7 | 3 |
| 6 | 27 | 23 | 10 | |
| 8 | 50 | 33 | ||
| 10 | 83 |
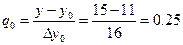
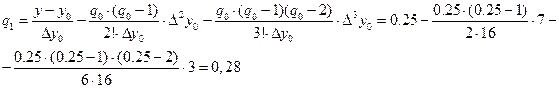
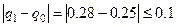Þ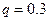 
Так как требуемая точность достигнута, то можно вычислить значение аргумента:
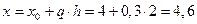
Обратное интерполирование на основе 2ИФН
Обратное интерполирование на основе 2ИФН осуществляется по аналогичным формулам:
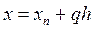
где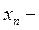 
координата ближайшей узловой точки.
,
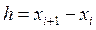
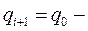
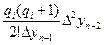
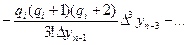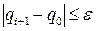
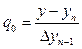
где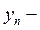 
координата ближайшей узловой точки, 
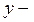заданное значение.
Решение дифференциальных уравнений
Метод Эйлера
В основе метода Эйлера (метод ломаных) лежит идея графического построения решения дифференциальных уравнений, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.
|
|
|
Пусть дано дифференциальное уравнение:
с начальными условиями:
.
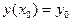Выбрав достаточно малый шаг h, строится система равноотстоящих точек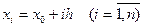 
.
В методе Эйлера приближенные значения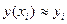 
вычисляются последовательно по формулам:
.
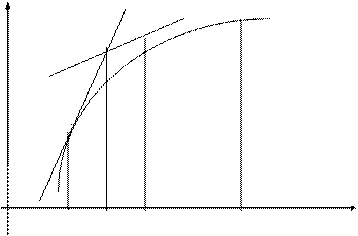
При этом искомая интегральная кривая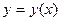 
, проходящая через точку 
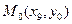, заменяется ломанной 
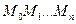с вершинами 
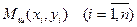; каждое звено 
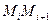этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения 
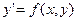, которая проходит через точку 
y
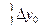
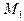
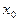
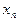
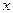
Первая улучшенная формула Эйлера
Пусть дано дифференциальное уравнение:
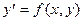
с начальными условиями:
.
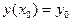Решение в каждой точке 
определяется по формуле:
,
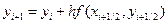где
.
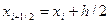
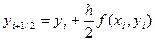Геометрически это означает, что отрезок ломанная между точками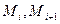 
заменяется на два отрезка 
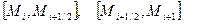. Направление первого отрезка совпадает с направлением интегральной кривой в точке 
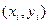, а направление второго отрезка определяется направлением интегральной кривой в вспомогательной точке 
.
|
|
|
Вторая улучшенная формула Эйлера
Пусть дано дифференциальное уравнение:
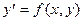
с начальными условиями:
.
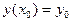Решение в каждой точке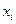 
определяется по формуле:
,
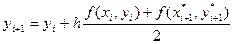где
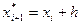
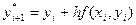
Геометрически это означает, что определяется направление интегральной кривой в исходной точке 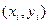и во вспомогательной точке 
, а в качестве окончательного направления ломаной берется среднее этих направлений.
Метод Рунге–Кутты
Наибольшее применение на практике получил метод Рунге–Кутты 4-го порядка:
,
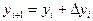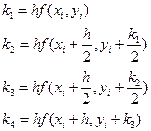
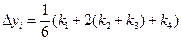
Дата добавления: 2019-07-15; просмотров: 619; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!