Интерполяционная формула Лагранжа.

Математические методы

Методические указания

 

Интерполирование методами Ньютона для равноотстоящих точек

Постановка задачи

На отрезке 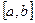 заданы  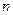значений аргумента  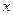и соответствующие им значения функции

f(x₀)=y₀; f(x₁)=y₁; …; f(x_n)=y_n.

Требуется построить функцию F(x), которая бы принимала в точках 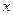 те же значения, что и :

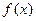F (x₀)=y₀; F (x₁)=y₁… F (x_n)=y_n

Это необходимо для решения следующих задач:

1. Задача интерполяции. Суметь по полученной функции вычислить значения F(z), где z ,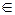

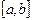z 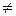x_i при i=0,n

2. Задача экстраполяции. Суметь по полученной функции вычислить F(z), где z .

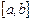Все существующие интерполяционные формулы содержат в себе конечные разности различных порядков.

Введём понятие конечных разностей.

Конечные разности различных порядков.

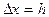       - фиксированная величина приращения аргумента

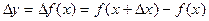        - называется первой конечной разностью функции y, или конечной разностью первого порядка.

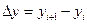                                                                    (1.1)

Вторая конечная разность, или конечная разность второго порядка:

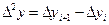                                                              (1.2)

Третья конечная разность, или конечная разность третьего порядка:

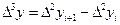                                                             (1.3)

Конечная разность n-го порядка:

                                                             (1.4)

 

Конечные разности различных порядков удобно располагать в форме горизонтальной таблицы разностей

x	y
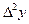
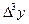
x0	y0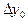
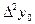
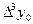
x1	y1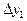
...	...	...	...	...

 

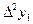
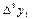
Пример.

Построить горизонтальную таблицу разностей для функции

                  y = f(x) = x²

при шаге 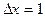, начальном значении x₀ = 0, конечном значении x₆=5.

Решение.

x	y
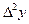
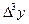
0	0	1	2	0
1	1	3	2	0
2	4	5	2	0
3	9	7	2
4	16	9
5	25

 

Первая интерполяционная формула Ньютона.

Пусть для функции y=f(x) заданы значения y_i=f(x_i) для равноотстоящих значений независимой переменной x_i=x₀+i*h (i=0,n) , где 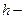 шаг интерполяции.

Требуется подобрать полином P_n(x) степени не выше 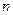, принимающий в точках x_i значения P_n(x_i)=y_i (i=0,n)

Первая интерполяционная формула Ньютона (1ИФН).

,

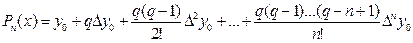где q= .

Пример.

Построить интерполяционный полином Ньютона для функции y= 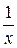 на отрезке  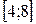c шагом h=1 и определить значение в точке x=4,4.

 

Решение. Построим горизонтальную таблицу разностей.

x	y
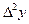
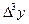
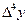
4	0,25	-0,05	0,017	-0,008	0,005
5	0,2	-0,033	0,009	-0,003
6	0,167	-0,024	0,006
7	0,143	-0,018
8	0,125

 

Таким образом, при наличии 5 точек максимальный порядок существующей конечной разности =4, максимальная степень полинома =4.

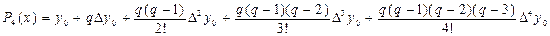
Определим значение в точке x=4,4. Узловые точки x₀=4, h=1, тогда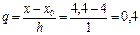

Для сравнения: точное значение функции в указанной точке = 0,22727.

Вторая интерполяционная формула Ньютона.

Первая интерполяционная формула Ньютона практически неудобна для интерполирования значений вблизи конца таблицы. В этом случае обычно применяется вторая интерполяционная формула Ньютона (2ИФН).

 

,

 

 

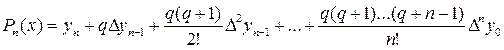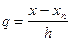
Как первая, так и вторая формула Ньютона могут быть использованы для экстраполирования функции, т.е. для нахождения значений функции y для значений аргументов x, лежащих вне пределов таблицы.

Если x< x₀, то лучше применять первую интерполяционную функцию Ньютона.

Если x> x_0, то лучше применять вторую интерполяционную функцию Ньютона.

1ИФН используется для интерполирования вперёд и экстраполирования назад.

2ИФН используется для интерполирования назад и экстраполирования вперёд.

Интерполяционная формула Лагранжа.

Пусть на отрезке [a; b] даны n+1 различных значений аргумента x: x₀, x₁,…, x_n

и известны соответствующие их значению функции y= f( x) : f( x₀)= y₀, f( x₁)= y₁, f(x_n)=y_n. Требуется построить полином 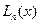 степени не выше 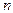, имеющий в заданных узлах  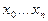те же значения, что и функция , т.е. 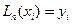 при i=1, n

 

;

 

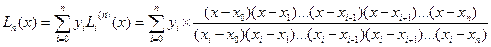где  –коэффициенты Лагранжа.

 

Для вычисления лагранжевых подмножеств удобно составлять следующую таблицу разности:

---

Дата добавления: 2019-07-15; просмотров: 90; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!