Уравнение плоской волны, распространяющейся в произвольном направлении
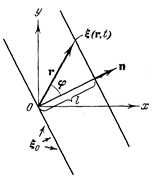 Найдем уравнение плоской волны, распространяющейся в направлении, образующем с осями координат x , y , z углы α, β, γ. Пусть колебания в плоскости, проходящей через начало координат (рис. 3.1), имеют вид
Найдем уравнение плоской волны, распространяющейся в направлении, образующем с осями координат x , y , z углы α, β, γ. Пусть колебания в плоскости, проходящей через начало координат (рис. 3.1), имеют вид
x =
a cos ( w
t + a )
Возьмем волновую поверхность (плоскость), отстоящую от начала координат на расстояние
l. Колебания в этой плоскости будут отставать от колебаний (3.1) на время τ =
l/υ
:

 x = a cos [ w( t − ) + a ] = a cos ( wt − kl + a ).
x = a cos [ w( t − ) + a ] = a cos ( wt − kl + a ).
(k = ω/υ; см. формулу (2.7)).
Выразим l через радиус-вектор точек рассматриваемой поверхности. Для этого введем единичный вектор n нормали к волновой поверхности. Из рис. 3.1 видно, что скалярное произведение n на радиус-вектор r любой из точек поверхности равно l:
nr = rcos φ=l.
Заменим в (3.2)
l через
nr :
x = a cos ( wt − knr + a )
Вектор
k = kn ,
равный по модулю волновому числу
k =2π/λ и имеющий направление нормали к волновой поверхности, называется волновым вектором. Таким образом, уравнение (3.3) можно представить в виде
x ( r, t ) = a cos ( wt − kr + a )
Мы получили уравнение плоской незатухающей волны, распространяющейся в направлении, определяемом волновым вектором k. Для затухающей волны нужно добавить в уравнение множитель e–γl = e–γ nr.
Функция (3.5) дает отклонение от положения равновесия точки с радиусом-вектором r в момент времени l (r определяет равновесное положение точки). Чтобы перейти от радиуса-вектора точки к ее координатам х , у , z , выразим скалярное произведение kr через компоненты векторов по координатным осям:
kr = kxx + kyy + kzz .
Тогда уравнение плоской волны примет вид
x (x , y , z, t ) = a cos ( wt − kxx – kyy – kzz + a )


Здесь

Функция (3.6) дает отклонение точки с координатами
х , у , z в момент времени
t. В случае, когда
n совпадает с
ex,
kx =
k,
ky =
kz = 0 (и уравнение (3.6) переходит в (2.8). Очень удобна запись уравнения плоской волны в виде
x = Re aei (ωt-kr+α)
Знак Re обычно опускают, подразумевая, что берется только вещественная часть соответствующего выражения. Кроме того, вводят комплексное число
â = ae iα,
которое называют комплексной амплитудой. Модуль этого числа дает амплитуду, а аргумент – начальную фазу волны Таким образом, уравнение плоской незатухающей волны можно представить в виде
x = â ei (ωt-kr)
Преимущества такой записи выяснятся в дальнейшем.
Волновое уравнение
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции (3.6), описывающей плоскую волну. Продифференцировав эту функцию дважды по каждой из переменных, получим
Сложение производных по координатам дает
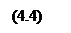
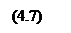
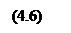
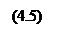

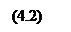

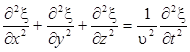 Сопоставив эту сумму с производной по времени и заменив k2/ω2 через 1/υ2 (см. (2.7)), получим уравнение
Сопоставив эту сумму с производной по времени и заменив k2/ω2 через 1/υ2 (см. (2.7)), получим уравнение
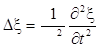 Это и есть волновое уравнение. Его можно записать в виде
Это и есть волновое уравнение. Его можно записать в виде
где Δ – оператор Лапласа.
Легко убедиться в том, что волновому уравнению удовлетворяет не только функция (3.6), но и любая функция вида
|
| | | f(x, y, z, t)=f(wt − kxx – kyy – kzz + a)
| |
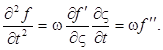
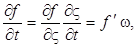 Действительно, обозначив выражение, стоящее в скобках в правой части (4.4), через ς, имеем
Действительно, обозначив выражение, стоящее в скобках в правой части (4.4), через ς, имеем
Аналогично
Подстановка выражений (4.5) и (4.6) в уравнение (4.2) приводит к выводу, что функция (4.4) удовлетворяет волновому уравнению, если положить υ=ω/k.
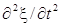 Всякая функция, удовлетворяющая уравнению вида (4.2), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при , дает фазовую скорость этой волны.
Всякая функция, удовлетворяющая уравнению вида (4.2), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при , дает фазовую скорость этой волны.
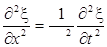 Отметим, что для плоской волны, распространяющейся вдоль оси х , волновое уравнение имеет вид
Отметим, что для плоской волны, распространяющейся вдоль оси х , волновое уравнение имеет вид
Дата добавления: 2019-07-15; просмотров: 406; | Поделиться с друзьями:
|

Мы поможем в написании ваших работ!
 Найдем уравнение плоской волны, распространяющейся в направлении, образующем с осями координат x , y , z углы α, β, γ. Пусть колебания в плоскости, проходящей через начало координат (рис. 3.1), имеют вид
Найдем уравнение плоской волны, распространяющейся в направлении, образующем с осями координат x , y , z углы α, β, γ. Пусть колебания в плоскости, проходящей через начало координат (рис. 3.1), имеют вид
 x = a cos [ w( t − ) + a ] = a cos ( wt − kl + a ).
x = a cos [ w( t − ) + a ] = a cos ( wt − kl + a ).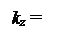


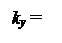
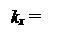
 Функция (3.6) дает отклонение точки с координатами х , у , z в момент времени t. В случае, когда n совпадает с ex, kx = k, ky = kz = 0 (и уравнение (3.6) переходит в (2.8). Очень удобна запись уравнения плоской волны в виде
Функция (3.6) дает отклонение точки с координатами х , у , z в момент времени t. В случае, когда n совпадает с ex, kx = k, ky = kz = 0 (и уравнение (3.6) переходит в (2.8). Очень удобна запись уравнения плоской волны в виде

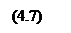
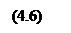
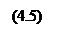

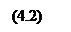


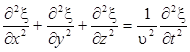 Сопоставив эту сумму с производной по времени и заменив k2/ω2 через 1/υ2 (см. (2.7)), получим уравнение
Сопоставив эту сумму с производной по времени и заменив k2/ω2 через 1/υ2 (см. (2.7)), получим уравнение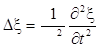 Это и есть волновое уравнение. Его можно записать в виде
Это и есть волновое уравнение. Его можно записать в виде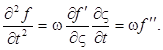
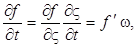 Действительно, обозначив выражение, стоящее в скобках в правой части (4.4), через ς, имеем
Действительно, обозначив выражение, стоящее в скобках в правой части (4.4), через ς, имеем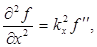
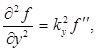
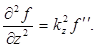
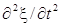 Всякая функция, удовлетворяющая уравнению вида (4.2), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при , дает фазовую скорость этой волны.
Всякая функция, удовлетворяющая уравнению вида (4.2), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при , дает фазовую скорость этой волны.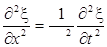 Отметим, что для плоской волны, распространяющейся вдоль оси х , волновое уравнение имеет вид
Отметим, что для плоской волны, распространяющейся вдоль оси х , волновое уравнение имеет вид
