Пример использования числовых характеристик матриц
Знание собственных значений матрицы и ее проекторов позволяет выполнять вычисления аналитических функций получающихся, например, при решениях систем линейных дифференциальных уравнений, при исследованиях эквивалентных матричных преобразований и пр.
Для примера построим матрицу с заданными собственными значениями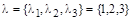 
и собственными векторами, основанными на векторах 
.
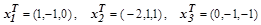Сначала необходимо убедиться в линейной независимости исходных векторов и добиться того, чтобы левые и правые одноименные собственные векторы оказались ортогональными, т.е.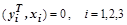 
. Проверка линейной независимости может быть объединена с процессом ортогонализации заданной системы векторов методом Грама-Шмидта.
Для заданных векторов построим систему векторов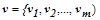 
таких, что 
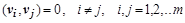, следующим образом:
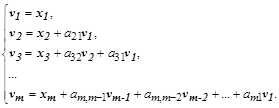
Откуда последовательно находятся коэффициенты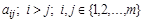 
:
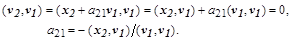
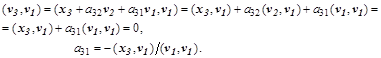
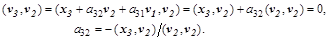
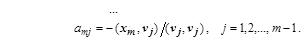
Взаимной ортогональности векторов v можно было бы добиваться и так, чтобы каждый 
был ортогонален каждому 
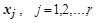, положив 
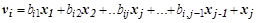и приравняв нулю скалярные произведения 
:
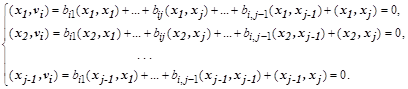
Определитель этой системы называют определителем Грама:
,
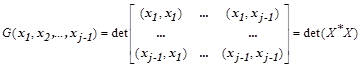где 
- матрица, в общем случае комплексно сопряженная с матрицей
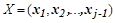, составленной из заданных векторов.
Если грамиан положителен, а он всегда неотрицателен, то векторы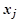 
линейно независимы, а если равен нулю, то зависимы. Это один из способов проверки конкретного набора векторов на их линейную независимость.
|
|
|
Для заданного выше набора векторов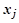 
определитель произведения матрицы X на транспонированную X * будет равен
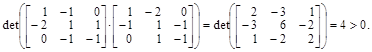
Таким образом, заданная система векторов линейно независима. Для построения ортонормированной системы векторов последовательно вычислим коэффициенты и ортогональные векторы:
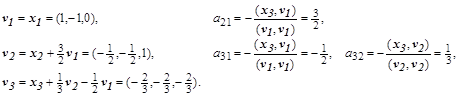
После нормирования векторы образуют правую систему собственных векторов. Транспонированная Т-матрица с этими векторами есть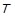 
-матрица ( 
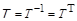); ее строки являются собственными левосторонними векторами:
.
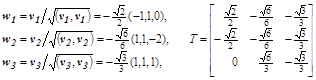Внешнее (матричное) произведение каждого нормированного вектора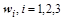 
самого на себя дает нам проекторы искомой матрицы:
Умножая каждое собственное значение 
из заданного набора на свой проектор и суммируя, получим:
.
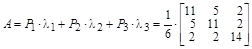Аналогично получается обратная матрица:
.
С помощью этих же проекторов вычисляется любая аналитическая функция, аргументом которой является матрица A:
.
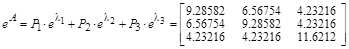Оценка величины и нахождение собственных значений
Краткое рассмотрение основных теоретических положений линейной алгебры позволяет сделать следующие выводы: для успешного решения систем линейных алгебраических уравнений и вычислений матричных функций необходимо уметь находить ее собственные значения и собственные векторы.
|
|
|
Для любой матрицы A с действительными компонентами и любого ненулевого вектора v существует отношение Рэлея, связывающее скалярное произведение векторов v и Av с минимальным и максимальным собственными значениями:
.
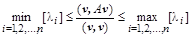К высказанному необходимо сделать еще ряд замечаний, связанных со случаями, когда исходная матрица имеет кратные собственные значения или оказывается вырожденной.
Характеристическое уравнение матрицы A с кратным корнем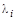 
можно записать в виде
.
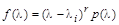На основании этой записи можно составить минимальное характеристическое уравнение 
, для которого матрица A также является корнем:
.
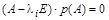Особенности в части определения собственных значений и векторов обычно возникают в несимметричных матрицах (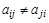 
). Некоторые из них никакими подобными преобразованиями не удается свести к диагональной. Например, не поддаются диагонализации матрицы n-го порядка, которые не имеют n линейно независимых собственных векторов. Однако любаяматрица A размера 
с помощью преобразования подобия может быть приведена к прямой сумме жордановых блоков или к канонической жордановой форме:
|
|
|
,
где A – произвольная матрица размера 
;
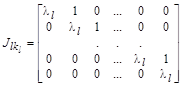– жорданов блок размера 
;
V – некоторая невырожденная матрица размера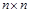 
.
Характеристическое уравнение жорданова блока размера 
независимо от количества единиц в верхней диагонали записывается в виде произведения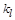 
одинаковых сомножителей и, следовательно, имеет только 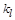кратных корней:
.
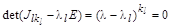Если выразить матрицу V в форме вектора с компонентами в виде векторов-столбцов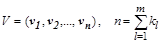 
, то из равенства AV=VJ для каждого жорданового блока следует соотношение
.
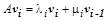Здесь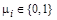 
в зависимости от структуры верхней диагонали, в которой может быть либо ноль, либо единица. Если жордановы блоки имеют размер 
, то мы имеем случай симметричной матрицы или матрицы с различными собственными значениями.
При поиске решений систем линейных уравнений с несимметричными матрицами, последние стремятся теми или иными приемами свести к выражению с симметричными матрицами.
Один из возможных подходов к решению несимметричных линейных систем состоит в замене исходной системы эквивалентной системой:
.
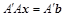Недостаток этого подхода состоит в том, что мера обусловленности произведения матрицы A на свою транспонированную, оцениваемая отношением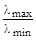 
, оказывается больше, чем у матрицы A.
|
|
|
Под мерой обусловленности понимают отношение наибольшего собственного значения матрицы к наименьшему. Это отношение влияет на скорость сходимости итерационных процедур при решении уравнений.
Итак, основными алгебраическими системами уравнений можно считать неоднородные системы уравнений с симметричными матрицами коэффициентов.
Литература
1. Вержбицкий В.М. Основы численных методов: Учебник для вузов – 3-е изд. М: Высшая школа, 2009. – 840 с.
2. Самарcкий А.А. Задачи и упражнения по численным методам. Изд. 3 Изд-во: КомКнига, ЛКИ, 2006. – 208 с.
3. Турчак Л.И., Плотников П.В. Основы численных методов. Изд-во: ФИЗМАТЛИТ®, 2003. – 304 с.
4. Хеннер Е.К., Лапчик М.П., Рагулина М.И. Численные методы. Изд-во: «Академия/Academia», 2004. – 384c.
5. Чистяков С.В. Численные и качественные методы прикладной математики. СПб: 2004. – 268 с.
Дата добавления: 2019-07-15; просмотров: 122; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!