Ортогональные матрицы из собственных векторов
Из правых собственных векторов можно составить матрицу T, а из левых – матрицу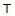 
, которые обладают уникальными свойствами по отношению к матрице A.
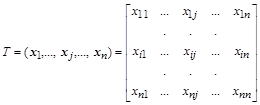
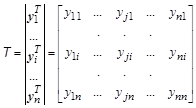
Умножив матрицу A слева на матрицу 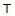, а справа – на матрицу T , после несложных преобразований получим:
.
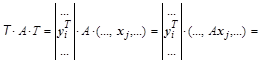
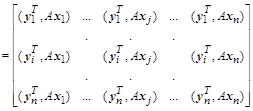Каждое скалярное произведение 
в матрице, принимая во внимание линейную независимость собственных векторов, полученных для различных собственных значений, можно преобразовать так:
Поэтому, результатом преобразования матрицы A будет диагональная матрица с собственными значениями, расположенными на диагонали:
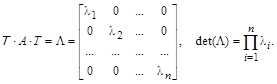
Если вместо A взять единичную матрицу и проделать аналогичные преобразования, то станет очевидным равенство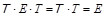 
, откуда следует 
. Последнее позволяет для преобразования матрицы A в диагональную обходиться только системой правых собственных векторов-столбцов:
Последнее показывает, что умножение матрицы A на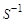 
слева и на S справа, где S – произвольная не особая матрица, преобразует ее в некоторую матрицу B, которая имеет определитель, равный определителю матрицы A. Такие преобразования матриц называют эквивалентными (подобными).
Продолжая использовать T-матрицу, несложно получить следующие важные результаты:
.
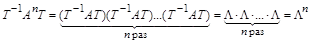Функции с матричным аргументом
Пусть теперь задана некоторая матричная функция от матрицы A:
.
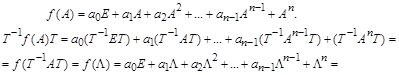
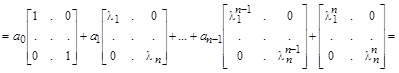
С другой стороны очевидно и обратное
,
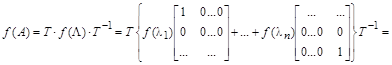
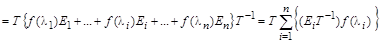где 
– матрица с одной единицей на i-том месте диагонали (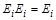 
).
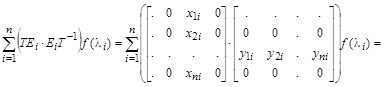
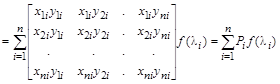
где 
– проекторы матрицы A, образуемые умножением одноименных правых и левых собственных векторов по правилам умножения прямоугольных матриц с размерами соответственно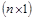 
и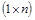 
. Сумма проекторов 
.
Проекторы обладают свойствами идемпотентных матриц, т.е. матриц, все степени которых равны первой. Для невырожденных проекторов (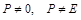 
) матрицы A ( 
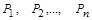) справедливо:
Представление функции от матрицы A в виде взвешенной суммы проекций называется спектральным разложением матричной функции по собственным значениям матрицы A:
.
Если в качестве матричных функций взять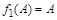 
и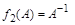 
, то их спектральные разложения будут следующими:
Вычисление проекторов матрицы
Проекторы матрицы можно также вычислить, воспользовавшись интерполяционным многочленом Лагранжа с матричным аргументом:
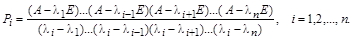
По известному спектру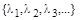 
проекторы матрицы можно найти и методом неопределенных коэффициентов. Для чего выбирают такие функции от матрицы A, которые вычисляются очевидным образом, например, такие:
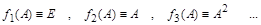
Записывая разложение для каждой функции, получим следующую систему линейных уравнений относительно проекторов:
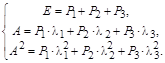
В случае, когда в спектре матрицы имеются кратные собственные значения, вычисление проекторов осуществляется по интерполяционным формулам Лагранжа, учитывающим еще и заданные значения производных в отдельных точках. Разложение матричной функции по значениям ее на спектре в этом случае имеет вид:
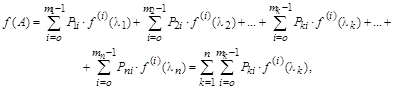
где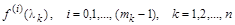 
– значения i-тых произ-водных функции в точках, соответствующих различным (не кратным) корням характеристического многочлена,
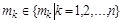– число кратных корней 
,
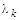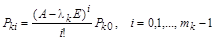– проекторы кратных корней, в выражении которых содержатся
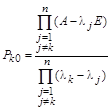– проекторы различных корней.
Дата добавления: 2019-07-15; просмотров: 151; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!