Линейный закон Гука (физические уравнения)
Для линейно-упругих изотропных тел физическими уравнениями являются соотношения для обобщенного закона Гука, известные из курса сопротивления материалов
,
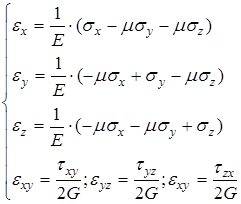где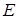 
и 
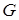- модули упругости при растяжении и сдвиге, а 
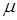- коэффициент Пуассона. Для изотропного материала они связаны зависимостью 
, так что независимых постоянных упругости для указанного материала имеется только две.
Запишем выражение для относительной объемной деформации элемента
,
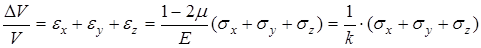где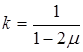 
- модуль объемной деформации материала.
Заметим, что при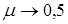 
модуль объемной деформации 
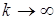, что, согласно выражению для относительной объемной деформации, соответствует материалу, не изменяющему объем при деформации (несжимаемый материал).
В случае плоского напряженного состояния система примет вид:
.
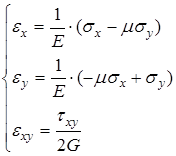Для плоской деформации ( 
) закон Гука записывается в несколько иной форме в виду наличия напряжения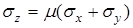 
:
,
.
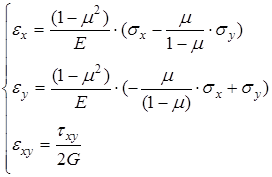Эта система совершенно аналогична системе, описывающей напряженное состояние, но содержит новые условные константы упругости
, 
,
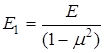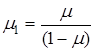причем легко проверить, что справедливо равенство
.
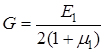С учетом введенных условных констант упругости физические соотношения для плоской деформации примут тот же вид, что и для случая плоского напряженного состояния, но в них надо заменить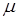 
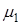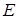на 
, на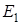 
.
Таким образом, любое решение приведенных выше уравнений для плоского напряженного состояния может быть применено и для соответствующего случая плоской деформации после замены действительных констант упругости данного материала на условные. Учитывая сказанное, в дальнейшем будем подразумевать под плоской задачей случай плоского напряженного состояния.
|
|
|
В полярной системе координат уравнения закона Гука остаются без изменения, меняются лишь индексы у напряжений и деформаций:
.
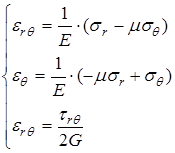Полученные уравнения дают возможность вычислить деформации, если известны напряжения. Назовем их законом Гука в прямой форме.
Преобразуем
.
В обратной форме
или, так как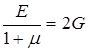 
, то
.
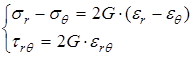Условия пластичности
При решении задач теории пластичности во многих случаях необходимо знать, при каких условиях материал в рассматриваемой точке переходит из упругого состояния в пластическое. Такие условия называются условиями пластичности. При линейном напряженном состоянии условие пластичности устанавливается опытным путем. В этом случае отлично от нуля только главное напряжение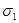 
и пластические деформации возникают, когда
; 
, (1.5.1)
где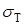 
- предел текучести при растяжении (постоянная величина для каждого материала). При чистом сдвиге условие пластичности, получаемое экспериментальным путем, имеет вид
|
|
|
,
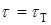где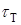 
- предел текучести при чистом сдвиге (также постоянная величина для каждого материала).
В общем случае плоского или объемного напряженных состояний экспериментально невозможно установить условия пластичности для бесконечного множества соотношений между составляющими напряжений. Поэтому условие пластичности для сложного напряженного состояния устанавливается гипотетическим путем с последующей экспериментальной проверкой.
Рассмотрим два условия пластичности, наиболее часто используемые в теории пластичности и достаточно правильно определяющие переход материала из упругого состояния в пластическое.
Первое условие – условие пластичности Треска - Сен-Венана – гласит, что пластические деформации в материале возникают, когда максимальные касательные напряжения достигают значения, равного пределу текучести при чистом сдвиге:
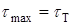. (1.5.2)
Максимальные касательные напряжения определяются формулой
: 
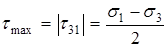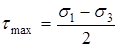. (1.5.3)
Подставляя сюда главные напряжения при линейном напряженном состоянии (1.5.1), в момент появления пластических деформаций получаем
|
|
|
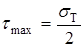. (1.5.4)
Сравнивая формулы (1.5.2) и (1.5.4) заключаем, что
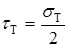. (1.5.5)
После подстановки выражений ( 1.5.3 ) и ( 1.5.5 ) в формулу ( 1.5.1 ) приходим к условию пластичности Треска-Сен-Венана в таком виде:
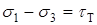. (1.5.6)
Второе условие – условие пластичности Мизеса-Генки – гласит, что пластические деформации в материале возникают, когда интенсивность касательных напряжений достигает некоторого постоянного для некоторого материала значения:
. (1.5.7)
Определим эту постоянную из результатов испытаний при простом растяжении. Подставляя в формулу
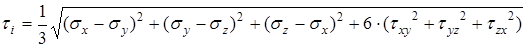(1.5.8)
главные напряжения (1.5.1), найдем значение интенсивности касательных напряжений при растяжении в момент появления пластических деформаций:
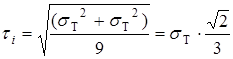. (1.5.9)
Сравнивая формулы (1.5.9) и (1.5.7), заключаем, что постоянная
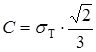. (1.5.10)
Подставляя выражения (1.5.8) и (1.5.10) в формулу (1.5.7), приходим к условию пластичности Губера-Мизеса-Генки в такой форме:
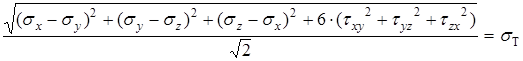(1.5.11)
Или
.
Оба рассмотренных условия пластичности дают весьма близкие результаты. Эксперименты несколько лучше подтверждают условие Губера-Мизеса-Генки. Кроме того, это условие удобнее с математической точки зрения, так как выражение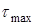 
через шесть составляющих напряжений очень громоздко, а 
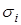выражается через эти составляющие сравнительно просто. Поэтому в теории пластичности чаще используется условие пластичности Губера-Мизеса-Генки.
|
|
|
Ассоциированный закон
Пластические деформации возникают при активном нагружении материала и не возникают при нейтральном нагружении и разгрузке.
Соотношения связи 
в теории пластичности формулируется обычно на основе принципа максимума Мизеса: при фиксированных параметрах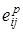 
для любого данного значения компонент приращений пластической деформации 
имеет место неравенство
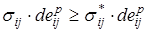, (1.5.12)
где 
- действительные компоненты напряжения, а 
- компоненты любого возможного напряженного состояния, допускаемого данной функцией нагружения:
.
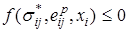Из принципа максимума Мизеса следует ассоциированный закон течения – закон направленности приращения пластической деформации (или скорости пластической деформации) по градиенту к поверхности нагружения.
В самом деле, предположим, что приращение пластической деформации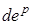 
не зависит от приращения напряжений.
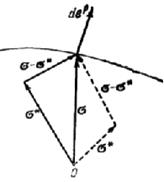
Рассмотрим рис. 1.7. Согласно (1.5.12) угол между векторам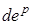и и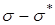 
должен быть не тупым. В силу произвольности вектора 
, не выходящего за поверхность нагружения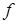 
, неравенство (1.5.12) может быть выполнено только в случае ортогональности 
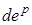к 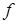, откуда имеем
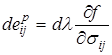или
, 
, 
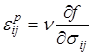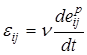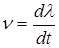. (1.5.13)
Выражение (1.5.13) определяет ассоциированный закон пластического течения.
Дата добавления: 2019-07-15; просмотров: 319; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!