Решение типового варианта здания 5
Задание. Найти площадь фигуры, ограниченной линиями, заданными уравнениями y = 2x– x2, y = 0, x = 3.
Решение.
1. Сделаем чертеж (рис. 5).
· Уравнение y = 2x – x2 задает параболу.
· Найдем координаты точки В(хв, ув) – вершины параболы.
· Из уравнения параболы следует, что а = –1, b = 2.
· Абсциссу параболы найдем по формуле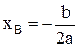 
, т.е. 
.
· Подставляя в уравнение параболы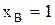 
, найдем ординату вершины.
· 
.
· Таким образом, вершина параболы находится в точке В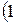 
; 
.
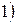· Так как а = – 1 < 0, то ветви параболы направлены вниз.
· Найдем абсциссы точек пересечения параболы с осью Ох (у = 0), решив уравнение
2х – х2 = 0,
х(2 – х) = 0,
х1 = 0 или 2 – х = 0,
х2 = 2.
· Таким образом, парабола пересекается с осью Ох в точках О(0; 0) и М(2; 0).
· Строим параболу (рис. 5).
· Уравнение у = 0 задает прямую, совпадающую с осью Ох.
· Прямая х = 3 проходит через точку P(3; 0) параллельно оси Оу.
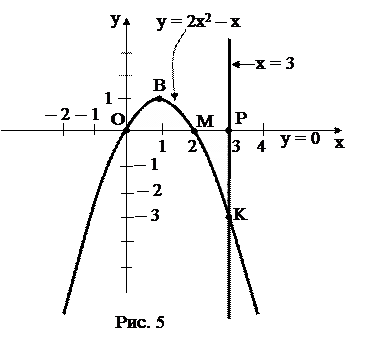
Найдем площадь построенной фигуры
· Фигура ОВMKP состоит их двух криволинейных трапеций ОВМ и МКР, расположенных соответственно выше и ниже оси Ох (рис. 5).
· Площадь фигуры ОВМ найдем исходя из геометрического смысла определенного интеграла с учетом формулы(1):
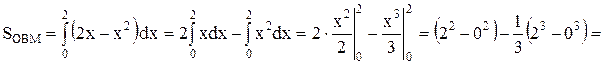
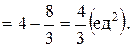
· Площадь фигуры МКР найдем исходя из геометрического смысла определенного интеграла с учетом формулы 2 (см стр. 6):
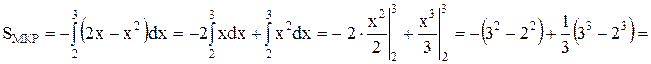
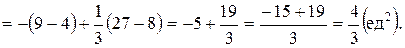
Тогда площадь искомой фигуры будет равна:
Sф = SОВМ + SМКР = 
.
Ответ: 
Задание 6. Вычислить длину дуги кривой.
|
|
|
| № варианта | Задание | № варианта | Задание |
| 1 | 
| 16 |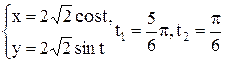 
|
| 2 |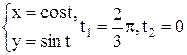 
| 17 | 
|
| 3 |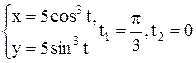 
| 18 |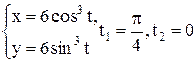 
|
| 4 |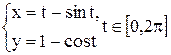 
| 19 | 
|
| 5 | 
| 20 |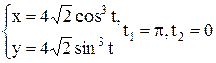 
|
Решение типового варианта здания 6
Задание. Вычислить длину дуги кривой, заданной параметрическими уравнениями
.
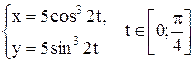Решение.
· Кривая задана параметрическими уравнениями.
· Найдем производные 
и 
:
;
.
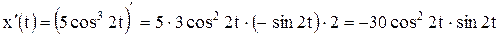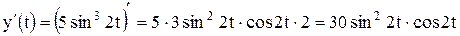· Преобразуем подынтегральную функцию:
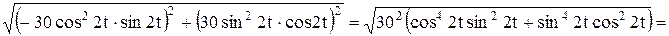
Согласно формуле 13 (см стр. 26), получаем:
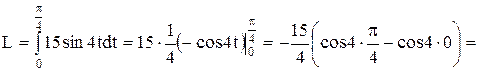
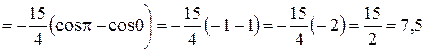(ед.).
Ответ: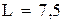 
(ед.).
Задание 7. Вычислить длину дуги кривой.
| № варианта | Задание | № варианта | Задание |
| 1 |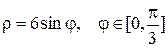 
| 16 |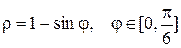 
|
| 2 | 
| 17 | 
|
| 3 | 
| 18 |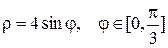 
|
| 4 |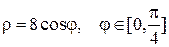 
| 19 | 
|
| 5 | 
| 20 |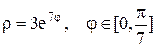 
|
Решение типового варианта задания 7
Задание. Вычислить длину дуги кривой, заданной уравнением
.
Решение.
· Кривая задана уравнением в полярных координатах.
· Найдем производную: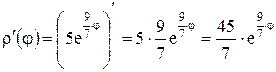 
.
· Преобразуем подынтегральную функцию:
= 
.
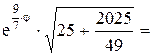
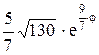· Получаем:
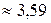(ед.).
Ответ: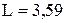 
(ед.).
Задание 8. Найти объем тела, полученного при вращении фигуры, ограниченной графиками, вокруг указанной оси.
| № варианта | Задание | № варианта | Задание |
| 1 | 
| 16 |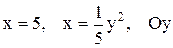 
|
| 2 | 
| 17 | 
|
| 3 |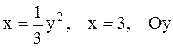 
| 18 |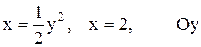 
|
| 4 |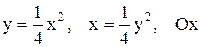 
| 19 | 
|
| 5 | 
| 20 | 
|
Решение типового варианта задания 8
|
|
|
Задание. Найти объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями y = x2 и x = y2.
Решение.
Сделаем чертеж.
· y = x2 – уравнение параболы, вершина которой расположена в точке О(0; 0), ветви направлены вверх, ось симметрии – ось Оу.
Строим параболу (см рис. 6).
| х | 0 | ±1 | ±2 |
| у | 0 | 1 | 4 |
· x = y2 – уравнение параболы, вершина которой расположена в точке О(0; 0); ось симметрии – ось Ох; ветви направлены в положительном направлении оси Ох.
| у | 0 | ±1 | ±2 |
| х | 0 | 1 | 4 |
Строим параболу (см. рис. 6):
2. Найдем абсциссы точек пересечения парабол, решив систему уравнений:
,
,
,
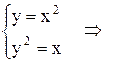
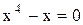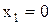или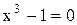 
,
,
,
.
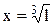Таким образом, абсциссы точек пересечения парабол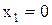 
и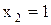 
.
3. Как видно из рис.6, искомый объем тела вращения равен разности двух объемов, образованных вращением вокруг оси Ох криволинейных трапеций ОСВА и ОDВА:
Vm = V1 – V2
Объемы V1 и V2 вычисляем по формулам:
(ед3.);
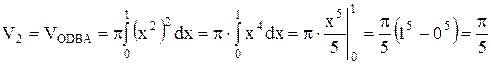(ед3.);
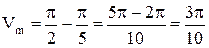(ед3.).
Ответ: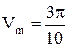 
(ед3.).
Задание 9. Найти объем тела, образованного вращением вокруг оси Ох плоской фигуры, ограниченной линиями.
|
|
|
Дата добавления: 2019-02-26; просмотров: 125; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!