Практическое занятие 3. Случайные величины
В электроэнергетике
3.1 Основные понятия, термины определения
Случайной величиной (СВ) называется величина, принимающая в результате опыта то или иное значение.
К случайным величинам в энергетике относятся такие параметры режима как спрос электрической мощности и энергии, отклонения частоты и напряжения в электрических сетях от номинальных значений, располагаемая мощность электростанций, мощность агрегатов в аварийном ремонте, длительности безаварийной работы и аварийного ремонта отдельных агрегатов и т.д.
Случайные величины можно разделить на два класса: дискретные и непрерывные.
Дискретная случайная величина может принимать только дискретные (разрозненные) значения, например число агрегатов, вышедших аварийно из работы. Это число в ограниченном интервале является конечным.
Законом распределения дискретной случайной величины наз. всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.
Для дискретных случайных величин распределение вероятностей различных их значений может быть наиболее просто задано с помощью таблиц распределения, в которых в верхней строке указываются все значения, принимаемые данной дискретной случайной величиной, а в нижней – вероятности соответствующих ей значений. Такая таблица наз. рядом распределения.
Если данная случайная величина всегда принимает одно из возможных значений, сумма вероятностей появления каждого из этих значений должна быть равной единице.
|
|
|
Значения непрерывных случайных величин могут изменяться непрерывно.
Для количественной оценки вероятностей как непрерывных, так и дискретных случайных величин вводят функцию распределения F(x), которая равна вероятности того, что данная случайная величина h (непрерывная или дискретная) попадает в интервал значений от -¥ до некоторого значения x
F(x) = P(-¥ £ h < x). (3.1)
Из определения следует, что F(-¥) = 0 и F(+¥) = 1.
Чтобы найти значения функции распределения дискретной СВ, можно использовать таблицы распределения, производя суммирование вероятностей слева направо.
Для непрерывных случайных величин функция распределения задается аналитически, если это возможно, или графически. По заданной функции распределения можно вычислить вероятности попадания случайной величины в определенный интервал значений (х1, х2). Если известны значения F(х1) и F(х2) для случайной величины h, то искомая вероятность попадания в интервал
P(х1 £ h < x2) = F(х2) - F(х1). (3.2)
|
|
|
Закон распределения вероятностей непрерывных случайных величин может быть определен заданием не функции распределения, а плотности распределения вероятностей j(х), которая представляет собой производную от функции распределения по значению случайной величины х:
j(х) = dF(x)/dx, (3.3)
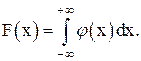(3.4)
Если плотность распределения вероятностей задана аналитически, то вероятность попадания непрерывной случайной величины в какой-либо интервал (х1, х2), где х1 < х2,
P(х1 £ h < x2) = F(х2) - F(х1).=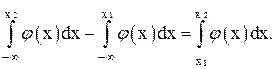 
(3.5)
В энергетике широко применяются случайные величины со следующими распределениями вероятностей:
а) биноминальное;
б) равномерное;
в) простейшее нормальное;
г) общее нормальное;
д) по закону Пуассона.
Биноминальное распределение дискретных СВ [2, с. 111-113, 266-267] встречается при повторении испытаний; его применяют при определении вероятностей различных значений аварийного снижения мощности в энергосистеме и аварийного выхода из строя различного числа агрегатов.
Математическое ожидание – среднее значение случайной величины, определяемое с учетом вероятностей ее отдельных значений. Математическое ожидание (МО) случайной величины h обозначается М(h).
|
|
|
Для дискретной случайной величины:
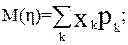(3.6)
для непрерывной случайной величины:
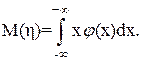(3.7)
Дисперсия случайной величины [2, с. 117-118] – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Дисперсия случайной величины h обозначается D( h) = = М[ h -М( h)] 2.
Стандартное (среднеквадратичное) отклонение случайной величины – квадратный корень из величины дисперсии, d(h):
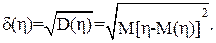(3.8)
Для дискретных случайных величин:
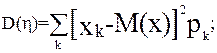(3.9)
для непрерывной случайной величины:
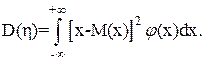(3.10)
Величина, имеющая неизменную плотность вероятности, называется равномерно распределенной непрерывной случайной величиной [2, с. 264-265]. Равномерное распределение служит основой метода статистических испытаний, применяющегося при определении резерва мощности, отказа срабатывания автоматики и т.п. При этом функция распределения изменяется по линейному закону. Если непрерывная случайная величина равномерно распределена только в интервале (a, b), то вероятность попадания в этот интервал равна единице, а j(х)=const:
|
|
|
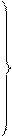
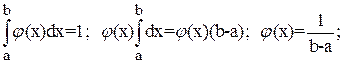
(3.11)
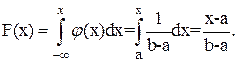
Вероятность попадания случайной величины в интервал (c, d), внутренний по отношению к интервалу (a, b), равна
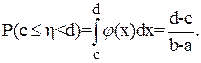(3.12)
Для многих электротехнических устройств время наработки на отказ имеет нормальное распределение. Кроме того, нормальное распределение используется при нахождении вероятностей ошибок прогнозирования нагрузки потребителей, отклонения нагрузки энергосистемы и ее отдельных частей от средних значений и т.п.
Простейшее нормальное распределение непрерывной случайной величины [2, с. 265]:
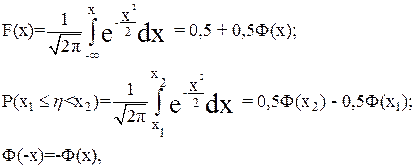(3.13)
где Ф(х) – интеграл вероятности [2, с. 272-273, таблица П3-3].
Общее нормальное распределение непрерывной случайной величины [2, с. 265 – 266]:
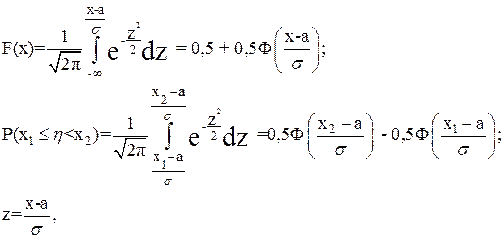(3.14)
где а = М(h);
s = d(h).
Распределение дискретной случайной величины, принимающей целочисленные значения от 0 до ¥ и распределенной по Пуассону: пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности появления в n испытаниях события А m раз, когда число n велико, а число р мало, используют распределение Пуассона [2, с. 140–142, 267].
Вероятность того, что дискретная случайная величина, распределенная по Пуассону, примет значение m, определяется по формуле:
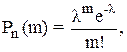(3.15)
где l - постоянная величина; l = n×p.
Параметр l в формуле (3.28) представляет собой математическое ожидание.
3.2 Задача 5
Условие [2, с. 113–114]
В энергетической системе, включающей четыре однотипных генератора, требуется найти вероятность одновременного выхода из строя нескольких генераторов, используя формулу биноминального распределения. Вероятность аварийного выхода каждого генератора q =0,02, вероятность рабочего состояния р = 0,98. Случайной величиной будем считать число агрегатов m, вышедших в аварию. Эта величина является дискретной и может принимать значения 0, 1, 2, 3, 4.
Решение
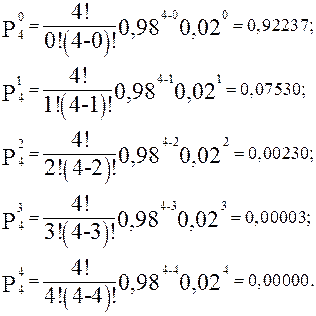
Результаты расчетов сведем в таблицу 2.
Т а б л и ц а 2 – Таблица распределения вероятностей числа аварийных
агрегатов
| Число аварийных агрегатов m | 0 | 1 | 2 | 3 | 4 |
Вероятность выхода в аварию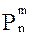 
| 0,92237 | 0,07530 | 0,00230 | 0,00003 | 0,00000 |
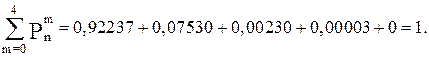
Найдем значения функции распределения вероятностей для х = 0, 1, 2, 3, 4, суммируя вероятности выхода агрегатов в аварию (см. таблицу 3.1) слева направо:
F(0) = 0;
F(1) = 0,92237;
F(2) = 0,99767;
F(3) = 0,99997;
F(4) = 1.
3.3 Задача 6
Условие [2, с. 115–122]
Пусть в энергосистеме возможны дефициты мощности 50, 100 и 150 МВт, причем вероятности этих дефицитов соответственно равны 0,001; 0,0004; 0,0002. Требуется определить МО недоотпуска энергии за год.
Решение
При постоянном дефиците 50 МВт недоотпуск электроэнергии за год составил бы 50×8760 МВт×ч, при дефиците 100 МВт – 100×8760 МВт×ч, при дефиците 150 МВт - 150×8760 МВт×ч. МО недоотпуска энергии за год равно:
М(h) = 50×8760×0,001 + 100×8760×0,0004 + 150×8760×0,0002 =
= 1051 МВт×ч.
3.4 Задача 7
Условие
Активная нагрузка предприятия распределена равномерно в диапазоне значений от 7 до 26 МВт. Определить:
а) вероятность нахождения нагрузки в диапазоне от 7 до 18 МВт:
б) значение нагрузки, вероятность превышения которой 7 %;
в) вероятность того, что нагрузка меньше 13 МВт.
Решение
а) для равномерного распределения интервал (a, b) = (7, 26);
(c, d) = (7, 18):
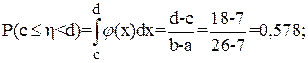
б) g(х) = 0,07 = 1 – F(x), откуда F(x) = 1 – 0,07 = 0,93:
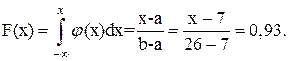
х = 0,93×(26-7) + 7 = 24,67 МВт – значение нагрузки, вероятность превышения которой равна 7 %;
в) вероятность того, что нагрузка меньше 13 МВт:
.
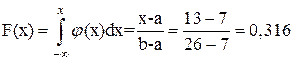3.5 Задача 8
Условие [2, с. 118–119]
Пусть среднемесячная максимальная нагрузка энергосистемы равна 1200 МВт. Примем, что отклонения суточных максимумов в рабочие дни данного месяца подчинены закону нормального распределения с известными числовыми характеристиками. Найти вероятность того, что суточный максимум будет колебаться в пределах 1250 ¸ 1300 Мвт. При этом дисперсия D(h) = 2500 Мвт2, а стандартное отклонение d(х) = 50 МВт.
Решение
а = М(h) = 1200 МВт; в соответствии с формулами (3.27) получим
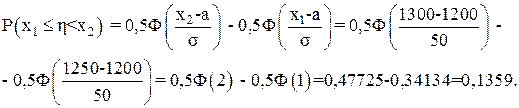
3.6 Задача 9
Условие
В состав энергосистемы входят 5000 понижающих трансформаторов 6-10/0,4 кВ, вероятность отказа каждого из которых составляет р = 0,0002. Найти вероятность того, что в аварийном состоянии одновременно будут находиться 3 трансформатора.
Решение
По условию n = 5000, р = 0,0002, m = 3. l = n×p = 5000×0,0002 = 1.
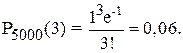
Вероятность того, что число событий на интервале времени Dt равно m, в соответствии с (3.15) определяется формулой
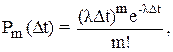(3.16)
где l - математическое ожидание дискретной случайной величины в единицу времени.
3.7 Задача 10
Условие
Число аварийных отключений электрооборудования подстанции в течение восьми месяцев равно десяти. При помощи распределения Пуассона определить вероятность того, что в течение четырех месяцев произойдет три отключения.
Решение
Dt = 4 мес.;
l = 10/8 = 1,25 откл./мес.;
lDt = 4×1,25 = 5 откл.
В соответствии с формулой (3.16) получим:
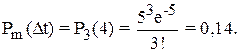
Список литературы
1. Соколов Г.А. Основы теории вероятностей [Электронный ресурс]: Учебник. – 2-е изд. – М.: ИНФРА-М, 2015. – 340 с. Режим доступа http://www.znanium.com/bookread2.php?book=405698.
2. Электрические системы. Математические задачи электроэнергетики [Текст]: Учебник для студентов вузов /Под ред. В.А. Веникова. - 2-е изд., перераб. и доп. - М.: Высшая школа, 1981. - 288 с.
3. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения [Текст]: Учеб. пособие для втузов. - 2-е изд., стер. - М.: Высшая школа, 2000. - 480 с.
4. Электрические системы и сети в примерах и иллюстрациях [Текст]: Учеб. пособие для электроэнерг. спец. /Под ред. В.А. Строева. – М.: Высшая школа, 1999. – 352 с.
5. Справочник по электроснабжению и электрооборудованию [Текст]: В 2-х т. Т. 1. Электроснабжение /Под общ. ред. А.А. Федорова. - М.: Энергоатомиздат, 1986. - 568 с.
6. Справочник по проектированию электроснабжения [Текст] /Под ред. Ю.Г. Барыбина и др. – М.: Энергоатомиздат, 1990. – 576 с.
Дата добавления: 2019-02-26; просмотров: 428; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!