Решение примерного варианта контрольной работы №2
Задача 1. Используя двойной интеграл, вычислить статический момент относительно оси Ox тонкой однородной пластинки, имеющей форму области D, ограниченной заданными линиями: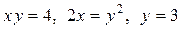 
. Построить чертеж области интегрирования.
Указание. Считать плотность вещества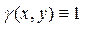 
.
Решение.
Область D (рис. 11) представляет собой криволинейный треугольник MNK, где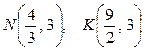 
. Для определения координат точки М решаем систему уравнений: 
Область D – правильная в направлении оси O х, она задается системой неравенств: 
где 
– это уравнения линий, ограничивающих область слева и справа.
Найдем статический момент пластинки MNK относительно оси Ox по формуле (11):
.
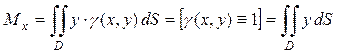Для вычисления двойного интеграла сводим его к повторному интегралу в соответствии с системой неравенств, задающих область D:
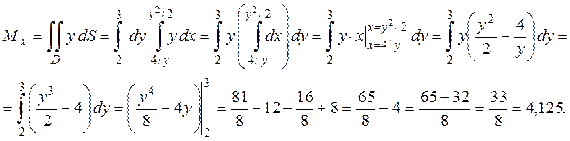
Ответы: Mx = 4,125 ед. стат. момента; область интегрирования на рисунке 11.
Задача 2. Используя тройной интеграл в цилиндрической системе координат, вычислить массу кругового цилиндра, нижнее основание которого лежит в плоскости xOy, а ось симметрии совпадает с осью Oz, если заданы радиус основания R = 0,5, высота цилиндра H = 2 и функция плотности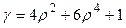 
, где r – полярный радиус точки.
Решение.
Массу кругового цилиндра можно вычислить, используя тройной интеграл по области V, по формуле (12):
,
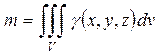где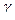 
– функция плотности, а V – область, соответствующая цилиндру.
Переходя к трехкратному интегралу в цилиндрических координатах, получаем:
|
|
|
,
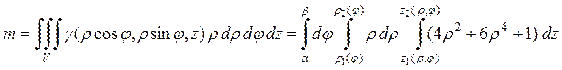где область интегрирования V (круговой цилиндр) можно задать системой неравенств: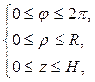 
при R = 0,5и H = 2.
Для определения массы цилиндра нужно вычислить трехкратный интеграл:
.
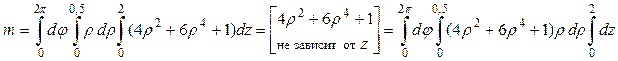Вычислим внутренний интеграл по переменной z: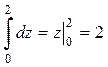 
.
Затем находим интеграл по переменной r:
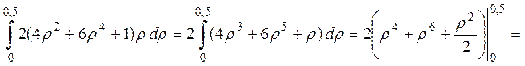
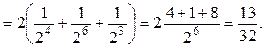
Третий этап – вычисление внешнего интеграла по переменной φ:
.
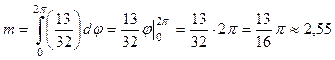Ответ: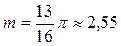 
ед. массы.
Задача 3. Вычислить работу силы 
при перемещении точки приложения силы вдоль заданной кривой L: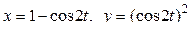 
от точки B до точки C, если значения параметра t в точках B и C заданы: 
.
Решение.
Для вычисления работы используем криволинейный интеграл II рода (формула (13)):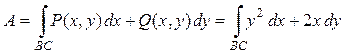 
.
Составленный криволинейный интеграл сводим к определенному интегралу, используя параметрические уравнения кривой ВС:
.
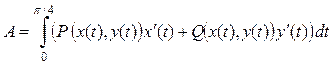Для заданной кривой получаем:
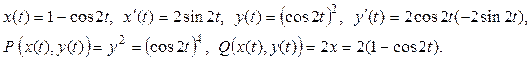
Таким образом, для нахождения работы нужно вычислить определенный интеграл:
Сделаем замену переменной в определенном интеграле:
, 
,
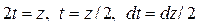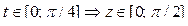тогда получим: 
.
Используем прием «подведение под знак дифференциала части подинтегральной функции»: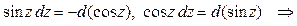 
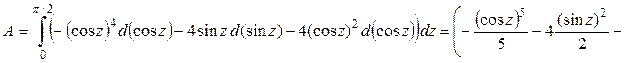
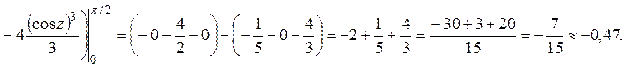
Ответ: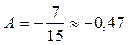 
ед. работы.
Задача 4. Задан радиус-вектор движущейся точки:
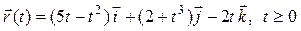. Найти векторы скорости и ускорения движения этой точки через 2 минуты после начала движения.
|
|
|
Решение.
Вектор-функция задана в виде: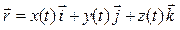 
.
Найдем первые и вторые производные ее проекций x(t), y(t) z(t) по аргументу t:
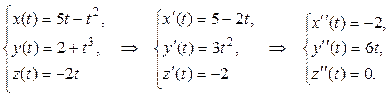
Найдем векторы скорости и ускорения движения точки по формулам (14) и (15):
.
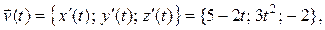
Через 2 минуты после начала движения векторы скорости и ускорения будут:
, 
.
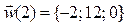Ответы: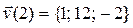 
, 
.
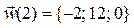Задача 5. Дано векторное поле 
и уравнение плоскости d: 3x + y + 2z – 3 = 0. Требуется:
1) найти поток поля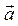 
через плоскость треугольника АВС где А, В, и С – точки пересечения плоскости d с координатными осями, в направлении нормали плоскости, ориентированной «от начала координат»; построить чертеж пирамиды ОАВС, где О – начало координат;
2) используя формулу Остроградского-Гаусса, вычислить поток поля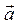 
через полную поверхность пирамиды ОАВС в направлении внешней нормали.
Решение.
1) Чтобы вычислить поток поля 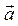через плоскость треугольника АВС используем формулу (16): ПАВС = 
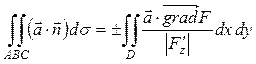, где D – проекция треугольника АВС на плоскость xOy, F – функция, задающая плоскость d, которой принадлежит треугольник АВС.
Для построения чертежа найдем точки А, В, и С пересечения плоскости d с координатными осями:
.
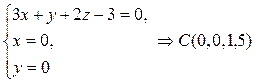Построим чертеж пирамиды, отложив на координатных осях точки А, В, С и соединив их с началом координат O (рис. 12).
|
|
|
Из уравнения плоскости d: 3x + y + 2z – 3 = 0, которое имеет вид F(x, y, z) = 0, находим
.
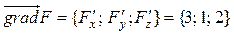Поскольку все три проекции градиента положительные, то этот вектор образует с координатными осями острые углы, т.е. направлен «от начала координат» по отношению к плоскости d.
Это означает, что вектор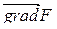 
и орт «внешней» нормали 
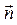, указанный в задаче, совпадают по направлению, поэтому вычисление потока через плоскость треугольника АВС сводится к вычислению двойного интеграла:
ПАВС = + 
(перед интегралом ставим знак «+»), где AO В – проекция треугольника ABC на плоскость xOy.
Для расстановки пределов интегрирования по треугольнику AO В (рис. 13) найдем уравнение прямой АВ на плоскости xOy:
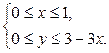
Вычислим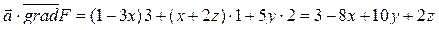 
и получим подинтегральную функцию, подставив 
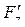= 2 и 
(из уравнения плоскости):
.
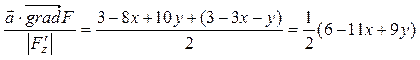Таким образом, поток поля 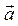через плоскость треугольника АВС:
.
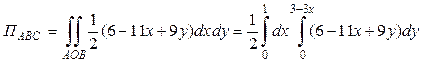Вычислим внутренний интеграл по переменной y:
Вычислим внешний интеграл по переменной х:
.
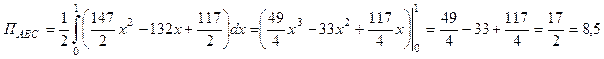2) Чтобы вычислить поток поля 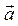через полную поверхность пирамиды ОАВС, воспользуемся формулой Остроградского-Гаусса:
.
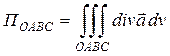Найдем дивергенцию этого поля по формуле (17):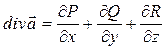 
. Для поля 
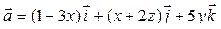получаем:
|
|
|
.
Вычислим поток поля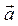 
через полную поверхность пирамиды ОАВС:
, где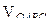 
– объем пирамиды ОАВС. Этот объем можно вычислить, следующим образом:
.
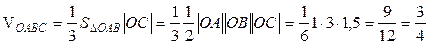В результате получаем: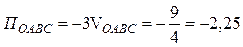 
.
Ответы: 1) П ABC = 8,5, рисунок 12; 2) ПОАВС = –2,25.
Задача 6. Проверить, является ли векторное поле силы 
потенциальным или соленоидальным. В случае потенциальности поля найти его потенциал и вычислить с помощью потенциала работу силы 
при перемещении единичной массы из точки M(0,1,0) в точку N(–1,2,3).
Решение.
Для проверки потенциальности векторного поля 
найдем его ротор по формуле (19):
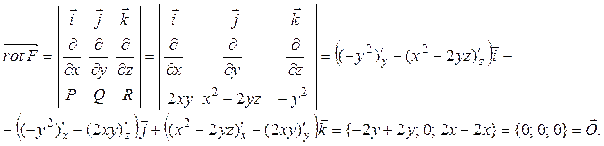
Следовательно, поле потенциально.
Для проверки соленоидальности поля найдем его дивергенцию по формуле (17):
.
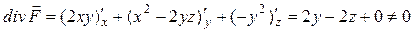Следовательно, поле не соленоидально.
Для нахождения потенциала U(x,y, z) векторного поля возьмем фиксированную точку В(0,0,0), текущую точку С(x, y, z) и вычислим криволинейный интеграл 
по ломаной В EKC, звенья которой параллельны осям координат и E(x,0,0), K(x,y,0) (см. рис. 8). По формуле (20) получим:
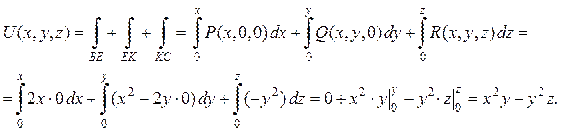
Получили потенциал поля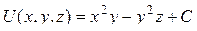 
, где С – произвольная постоянная. Для проверки решения найдем градиент потенциала 
: 
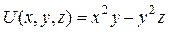. Следовательно, потенциал поля силы найден верно.
Найдем работу векторного поля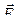 
при перемещении единичной массы из точки M(0,1,0) в точку N(–1,2,3) по формуле (21):
.
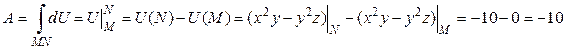Ответы: поле потенциально, не соленоидально;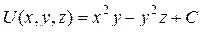 
, где С – произвольная постоянная; работа А = –10.
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. –М.: Айрис-пресс, 2003. – 288 с.
2. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 2 / Д.Т. Письменный. –М.: Айрис-пресс: Рольф, 2002. – 256 с.
3. Пискунов, Н.С. Дифференциальное и интегральное исчисление: учебник для втузов. В 2 т. Т. 1 / Н. С. Пискунов.– М.: Интеграл-Пресс, 2001.– 456 с.
4. Шипачев, В.С. Высшая математика: учебник для вузов / В.С. Шипачев.– М. : Высш. шк., 2007.– 479 с.
5. Данко, П.Е. Высшая математика в упражнениях и задачах: учебное пособие для втузов. В 2 ч. Ч.1 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова.– М.: Оникс: Мир и образование, 2005.– 304 с.
6. Данко, П.Е. Высшая математика в упражнениях и задачах: учебное пособие для втузов. В 2 ч. Ч.2 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова.– М.: Оникс: Мир и образование, 2005.– 416 с.
7. Шипачев, В.С. Задачник по высшей математике / В.С. Шипачев.– М. : Высш. шк., 2001.– 304 с.
8. Кручкович Г.И. Сборник задач и упражнений по специальным главам высшей математики: учебное пособие для втузов. / Г.И. Кручкович [и др.], под ред. Г.И. Кручковича. – М.: Высш. шк., 1970.– 512 с.
Дата добавления: 2019-02-22; просмотров: 220; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!