Малюнок 1.5 Схема визначення композиційної семантики
В цій схемі похідну стрілку Sem 0 ® Sem 1 можна тлумачити як уточнення (експлікацію) семантики.
Ця схема буде використана далі для введення аплікативної аксіоматичної семантики.
1.4 Властивості програмної алгебри
Побудована програмна алгебра дозволяє сформулювати властивості программ, досліджуючи властивості функцій цієї алгебри, заданих її термами (функціональними виразами). Доведемо декілька таких властивостей.
Зауваження 1.6 В програмній алгебрі рівність розглядається як рівність функцій.
Лема 1.1 Доведемо властивість асоціативності послідовного виконання, тобто справедливість наступної тотожності (f, g, h Î FS):
(f·g) ·h=f· (g·h).
Доведення. Оскількі в лемі формулюється рівність функцій, то слід довести, що на одному і тому ж даному обидві функції мають бути 1) одночасно невизначеними, або 2) одночасно визначеними і в цьому випадку давати однакові результати (сильна рівність функцій). Використовуючи позначення f s(st)¯ (фунція f s визначена на st) та f s(st) (фунція f s не визначена на st) наведене формулювання рівності можна задати наступним чином:
f s 1=f s 2 тоді і тільки тоді, коли для довільного стану stÎState
1) ((fs1(st)& fs2(st)) або
2) (fs1(st)¯& fs2(st)¯& fs1(st)= fs2(st)).
Стосовно леми це означає:
(f·g)·h=f·(g·h) ) тоді і тільки тоді, коли для довільного стану stÎState
1)((f·g)·h)(st)& (f·(g·h))(st) або
2) ((f·g)·h)(st)¯& (f·(g·h))(st)¯& ((f·g)·h)(st)= (f·(g·h))(st))
Перейдемо до доведення. Беремо довільний стан stÎState. Спочатку доведемо, що якщо ((f·g)·h)(st), то (f·(g·h))(st). Дійсно, для ((f·g)·h)(st) маємо формулу h(g(f(st))). Тому значення ((f·g)·h)(st) буде не визначеним, якщо або f(st) не визначене, або g(f(st)) не визначене, або h(g(f(st))) не визначене. Але в кожному з цих трьох випадків буде невизначеним і значення (f·(g·h))(st). Має місце і зворотнє. Отже, якщо одне із значень ((f·g)·h)(st) або (f·(g·h))(st) не визначене, то і друге значення також не визначене, тому формула ((fs 1(st)& fs 2(st)) буде істинною. Зауважимо, що звідси випливає, що якщо значення одного із функціональних виразів є визначеним, то є визначеним і значення іншого функціонального виразу.
|
|
|
Отже, коли одне із значень буде визначеним, то тоді визначені обидва значення і вони будуть рівними, бо ((f·g)·h)(st)= h(g(f(st))) та (f·(g·h))(st)=h(g(f(st))).
Лема доведена▄
У подальшому не будемо детально аналізувати випадки невизначеності функцій, сподіваючись, що читач сам зможе такі ситуації проаналізувати.
Зауваження 1.7 Рівність функцій можна доводити як рівність їх графіків. Але це вимагає переозначення композицій з функціональних в теоретико-множинні терміни. Тут цього робити не будемо.
Далі доведемо наступне твердження.
Лема 1.2 (Про властивості циклу) Для довільних функцій f sÎFS і fbÎFB, та довільного стану stÎState мають місце наступні властивості:
|
|
|
· WH(fb,f s)= IF(fb, f s · WH(fb,f s), id).
· NumIt WH((fb, f s), st)=0 тоді і тільки тоді, коли fb(st)¯=false (це також означає, що WH(fb, f s)(st)= st).
· Якщо NumIt WH((fb, f s), st)>0, то
– fb(st)¯=true,
– WH(fb, f s)(st)= WH(fb, f s)( f s(st)) та
– NumIt WH((fb, f s), f s(st))= NumIt WH((fb, f s), st) – 1.
Доведення.
Спочатку доведемо першу властивість, що задає певну тотожність. Беремо довільний стан stÎState. Припустимо, що WH(fb, f s)(st) визначено. Можливі два варіанта:
1) fb(st)=false,
2) fb(st)=true.
У першому випадку тіло циклу не виконується (NumIt WH((fb, f s), st)=0), тому WH(fb,f s)(st)=st. При обчисленні IF(fb, f s· WH(fb,f s), id) (st) потрібно обчислити id(st), що дає також значення st. Тому лема для цього випадку справедлива.
У другому випадку визначеність WH(fb,f s)(st) означає, що є послідовність станів та значень предикату (тому NumIt WH((fb, f s), st))>0), яка задовольняє наступним умовам:
st0=st, st1=f s(st0), st2=f s(st1),…, stn=f s(stn-1), причому
fb(st0)=true, fb(st1)=true,…, fb(stn-1)=true, fb(stn)=false.
Розглянемо, яке значення має WH(fb,f s)(st1). Зрозуміло, що послідовність обчислень повторює вищенаведену послідовність, але початковим станом є st1. Тому WH(fb,f s)(st1)=stn. Звідси також випливає, що NumIt WH((fb, f s), st1)= n–1.
Подивимось тепер на обчислення функціонального виразу (праву частину тотожності)
|
|
|
IF(fb, f s· WH(fb,f s), id) (st).
Оскільки fb(st)=true, то
IF(fb, f s·WH(fb,f s), id)(st)= (f s·WH(fb,f s)) (st)= WH(fb,f s)(f s(st))=WH(fb,f s) (st1)= st n.
Таким чином, і в цьому випадку лема справедлива.
Аналогічно доводиться, що якщо визначена ліва частина тотожності, то буде визначена і права частина з тим самим результатом. Тотожність доведено. З цього доведення випливають і інші дві властивості, сформульовані в лемі▄
Зауваження 1.8 Тотожність WH(fb,f s)=IF(fb, f s·WH(fb,f s), id) стверджує, що WH(fb,f s) є розв’язком відносно X (можливо, одним із розв’язків) функціонального рівняння
X=IF(fb, f s · X, id).
Дослідження рівнять такого типу буде проведено у розділі, присвяченого рекурсії. ▄
Леми 1.1 та 1.2 характеризували властивості побудованої алгебри функцій A_Prog. Такіх властивостей є досить багато. Їх ідентифікація (формулювання) є важливою проблемою. Такі тотожності дозволяють робити еквівалентні перетворення програм з метою доведення їх властивостей, або проведення оптимізації, трансляції, інтерпретації і таке інше.
Перейдемо тепер до визначення підалгебр алгебри A_Prog. Серед різних можливих підалгебр виділимо підалгебру, яка індукована аналізом відношення розширення (збагачення) станів новими змінними з їх значеннями. Наприклад, знаючи, що sem_P(GCD)([Ma8, Na16])= [Ma8, Na8], запитаємо про значення sem_P(GCD)([Ma8, Na16, La9]), тобто про значення функції sem_P(GCD) на новому стані, який має нову змінну L. Більшість програмістів погодиться з тим, що результуючий стан буде просто розширенням попереднього результуючого стану цією новою змінною, тобто, що sem_P(GCD)([Ma8, Na16, La9])= [Ma8, Na8, La9]). Іншими словами, функція sem_P(GCD) є монотонною щодо відношення розширення станів Í. Монотонність функцій визначається наступним чином.
|
|
|
Функція fsÎFS називається монотонною, якщо з того, що fs(st)¯=str та stÍst¢ випливає, що fs(st)¯=str¢ та strÍstr¢. Підклас монотонних функцій позначимо MFS.
Така властивість функцій використовується програмістами при збільшені памяті комп’ютера, бо програми на збільшеній памяті будуть працювати так само (в усякому разі ми на це сподіваємось), як і на меншій памяті.
А чи є подібна властивість для функцій, породжених арифметичними виразами та умовами мови SIPL? Виявляється, при розширенні станів значення арифметичних функцій та предикатів не змінюється. Така властивість називається еквітонністю (“екві” означає “рівний”). Точне визначення наступне.
Функція fÎFA називається еквітонною, якщо з того, що f(st)¯=r та stÍst¢ випливає, що f(st¢)¯=r. Підклас еквітонних функцій позначимо EFA, підклас еквітонних предикатів – EFB.
Як бачимо, поняття монотонної та еквітонної функції є дуже важливими, тому подивимось на поведінку таких функцій стосовно композицій мови SIPL.
Виявляється (і зараз це буде доведено), що введені класи утворюють еквітонно-монотонну підалгебру
A_EM_Prog =<FNA, FNB, FNAB, E FA, E FB, M FS;
Sn, ASx, ·, IF, WH, xÞ, id>
алгебри функцій A_Prog.
Для цього потрібно довести, що класи E FA, E FB, M FS замкнені відносно заданих на них композицій.
Спочатку доведемо, що клас EFA замкнений відносно композицій алгебри A_Prog, заданих на EFA, тобто що він є замкненим відносно композиції суперпозиції S n та функції розіменування. Нехай f – n-арна функція з FNA, g1,…,gn ÎEFA. Треба довести, що Sn(f, g1,…,gn) ÎEFA. Беремо довільні st та st¢, такі що stÍst¢. Вважаємо також, що (Sn(f, g1,…,gn))(st)¯=r. Доведемо, що (Sn(f, g1,…,gn))(st¢)¯=r. Дійсно, враховуючи, що g1(st¢)= g1(st), …,gn(st¢)=gn(st) маємо
(Sn(f, g1,…,gn))(st¢)=f(g1(st¢),…,gn(st¢))= f(g1(st),…,gn(st))=r.
Неважко також переконатися, що функція розіменування є еквітонною функцією з класу EFA.
Аналогічно доводиться, що клас і еквітонних предикатів EFB замкнений відносно відповідних композицій суперпозиції.
Залишилося довести, що клас монотонних функцій MFS замкнений відносно композицій присвоєння, послідовного виконання, умовного оператора, циклу та тотожної функції. Розглянемо всі ці випадки (для довільних st та st¢, таких що stÍst¢).
1. Присвоєння. Нехай faÎEFA та ASx (fa)(st)¯=st r. За визначенням ASx (fa)(st)=st Ñ[xa fa(st)]. Обчислимо ASx (fa)(st¢), враховуючи, що для faÎEFA fa(st¢)=fa(st). Маємо
ASx (fa)(st¢)= st¢ Ñ[xa fa(st¢)]= st¢ Ñ[xa fa(st)].
Порівнюючи st Ñ[xa fa(st)] та st¢ Ñ[xa fa(st)] можна стверджувати, що st Ñ[xa fa(st)]Íst¢ Ñ[xa fa(st)], оскільки значення змінної x у цих станах є однакові, а stÍst¢.
2. Послідовне виконання. Нехай f s 1, f s 2ÎMFS та f s 1·f s 2(st)¯=st r. За визначенням, f s 1·f s 2(st)=f s 2(f s 1(st)). Обчислимо f s 1·f s 2(st¢), враховуючи, що f s 1, f s 2ÎMFS. Маємо f s 1·f s 2(st¢)= f s 2(f s 1(st¢)). Оскільки f s 1(st)Í f s 1(st¢), то і f s 2(f s 1(st))Í f s 2(f s 1(st¢)), що і треба було довести.
3. Умовний оператор. Нехай fbÎEFB, f s 1, f s 2ÎMFS та IF(fb, fs 1, fs 2)(st)¯=st r. За визначенням, IF(fb, fs 1, fs 2)(st) дорівнює f s 1(st), якщо fb(st)=true, або f s 2(st), якщо fb(st)=false. Обчислимо IF(fb, fs 1, fs 2)(st¢), враховуючи, що fbÎEFB (тобто fb(st¢)= fb(st)), а f s 1, f s 2 Î MFS. Тому, якщо fb(st¢)=true, то IF(fb, fs 1, fs 2)(st¢)= fs 1(st¢), і оскільки fs 1(st) Í fs 1(st¢), то IF(fb, fs 1, fs 2)(st)ÍIF(fb, fs 1, fs 2)(st¢). Аналогічно для випадку fb(st¢)=false отримуємо IF(fb, fs 1, fs 2)(st)ÍIF(fb, fs 1, fs 2)(st¢).
4. Цикл. Доведення випливає з того, що послідовності станів при обчисленні WH(fb,f s)(st¢) відповідають послідовності станів при обчисленні WH(fb,f s)(st), причому увесь час має місце співвідношення stiÍsti¢ (i=0,…, n).
5. Тотожна функція є монотонною з класу MFS.
Таким чином доведено наступну лему.
Лема 1.3 Еквітонно-монотонна алгебра A_EM_Prog є підалгеброю
алгебри функцій A_Prog.
Доведена лема дозволяє дати більш точний опис функцій, породжуваних мовою SIPL. Для цього слід показати, що алгебра A_ SIPL є підалгеброю алгебри A_EM_Prog. Слід переконатися, що функції-константи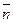 
та 
, 
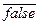є еквітонними функціями (що очевидно). Отже, справедливо наступне:
· якщо aÎAexp, то sem_A(a)ÎEFA ,
· якщо bÎBexp, то sem_B(b)ÎEFB ,
· якщо SÎStm, то sem_S(S)ÎMFS ,
· якщо PÎProg, то sem_P(P)ÎMFS .
Отримані твердження можна сформулювати у вигляді наступної теореми.
Теорема 1.2 Вирази та умови мовиSIPL породжують еквітонні функції, а програми та оператори – монотонні функції.
З теореми випливає, що якщо програма мови SIPL завершується з якимись результатами на певному стані, то вона завершиться і на розширеному стані, причому однакові змінні в обох результуючих станах будуть мати однакові результати.
Доведемо тепер коректність програми GCD. Позначимо функцію взяття найбільшого спільного дільника двох чисел як gcd.
Відзначимо, що оскільки у нас поки що є лише одна – композиційна семантика, то коректність програми доводиться відносно цієї семантики. Тому програмістські терміни слід тлумачити саме у термінах композиційної семантики. Так, завершуваність програми означає, що функція, яка задає семантику програми, визначена на відповідному стані, ітерація циклу – обчислення наступного члена послідовності станів, і так далі.
Теорема 1.3 (Про часткову коректність програми GCD) Нехай стан st такий, що M Þ(st)=m, N Þ(st)=n (m, n>0). Тоді, якщо sem_P(GCD)(st)¯=str, то M Þ(str)=N Þ(str)=gcd(m, n).
Зауваження 1.9 Згідно теореми 1.2 можна взяти стан, який має лише дві змінні – M та N. В цьому випадку теорему можна сформулювати більш просто:
якщо sem_P(GCD)( [Mam, Nan])¯= [Mar 1, Nar 2], то r 1=r 2=gcd(m, n).
Доведення.
Побудуємо семантичний терм функції sem_P(GCD).
Маємо
sem_P(GCD)=sem_P(begin while M¹N do if M>N then M:=M–N else N:=N–M end)=
=WH(S2(neq, MÞ, NÞ)),
IF(S2(gr, MÞ, NÞ),
ASM( S2(sub, MÞ, NÞ)),
ASN( S2(sub, NÞ, MÞ))
)
)
Таким чином, семантика програми задається семантичним термом з композицією циклу у якості головної операції. Для спрощення позначимо
p_g = S2(neq, MÞ, NÞ),
f_g = IF(S2(gr, MÞ, NÞ), ASM( S2(sub, MÞ, NÞ)), ASN( S2(sub, NÞ, MÞ))).
У цьому випадку sem_P(GCD)= WH(p_g, f_g).
Оскільки значення WH(p_g, f_g)(st) визначене, то NumItWH((p_g, f_g), st)³0. Нехай NumItWH((p_g, f_g), st)=k. Теорему будемо доводити індукцією за k (тобто, за кількістю ітерацій циклу). Індуктивна гіпотеза фактично повторює формулювання теореми:
якщо m >0, n >0, MÞ(st)=m, NÞ(st)=n, WH(p_g, f_g)(st)¯=str, то MÞ(str)=NÞ(str)=gcd(m, n).
База індукції. Нехай k=0. Згідно леми 1.2, p_g(st)¯=false та WH(p_g, f_g)(st)= st.
Що означає умова p_g(st)¯=false? Щоб це з’ясувати, проведемо наступні обчислення: p_g(st)=S2(neq, MÞ, NÞ)(st)=neq(MÞ(st), NÞ(st))= neq(m, n)=false. Це означає, що m=n, тому MÞ(st)=NÞ(st)= gcd(m, n).
Теорема виконується для цього випадку.
Крок індукції. Нехай теорема справедлива для всіх станів st таких, що NumItWH((p_g, f_g), st)=k (обчислення WH(p_g, f_g)(st) вимагає k застосувань функції f_g на відповідних станах). Доведемо, що тоді теорема буде справедлива для станів st, на яких обчислення WH(p_g, f_g)(st) вимагає k+1 кроків. В цьому випадку (згідно леми 1.2) це означає, що p_g(st)¯=true (тобто m¹n), WH(p_g, f_g)(st) = WH(p_g, f_g)(f_g (st)) та NumItWH((p_g, f_g), f_g (st))=k.
Проведемо обчислення f_g (st)= IF(S2(gr, MÞ, NÞ), ASM( S2(sub, MÞ, NÞ)), ASN( S2(sub, NÞ, MÞ)))(st).
Маємо два випадки:
1) S2(gr, MÞ, NÞ)(st)¯=true (це означає, що m>n). Тоді f_g (st)= ASM(S2(sub, MÞ, NÞ))(st)=stÑ[MaS2(sub, MÞ, NÞ)(st)]= stÑ[Ma sub(MÞ(st), NÞ(st)]=stÑ[Ma sub(m, n)]= stÑ[Ma m–n]. (Для стану st з двома змінними можна записати, що результат є [Mam, Nan] Ñ[Ma m–n]= [Ma m–n, Nan].)
2) S2(gr, MÞ, NÞ)(st)¯=false (це означає, що m£n, але враховуючи, що m¹n, маємо m < n). Тоді f_g (st)= AS N( S2(sub, NÞ, MÞ))(st)=stÑ[NaS2(sub, NÞ, MÞ)(st)]= stÑ[Na sub(NÞ(st), MÞ(st)]=stÑ[Na sub(n, m)]= stÑ[Na n–m]
(Для стану st з двома змінними можна записати, що результат є [Mam, Nan] Ñ[Na n–m]= [Mam, N a n–m].)
З теорії чисел випливає, що при вказаних умовах gcd(m, n)= gcd(m, m–n), якщо m > n, та gcd(m, n)= gcd(n–m, n), якщо m < n.
Дійсно, не обмежуючи загальності, розглянемо випадок m>n. Тут M має значення m–n , а N – n. Покажемо, що gcd(m, n)= gcd(m, m–n). Для цього слід показати, що множина спільних дільників m і n і множина спільних дільників m–n і n – співпадають. Нехай q – спільний дільник m і n, тобто m = q*k , n = q*r, для деяких натуральних чисел k, r. Тоді m–n = q*k – q*r = q*(k–r), тобто q – спільний дільник m–n і n. Аналогічним чином доводиться і зворотне твердження. Оскільки множини спільних дільників двох пар чисел співпадають, то і найбільший спільний дільник у них теж співпадає.
Отже, в стані st 1=f_g(st) значення змінних M та N додатні (більше нуля), та дорівнюють відповідно m та m–n, або n–m та n. Таким чином, для обох випадків маємо MÞ(st 1)>0, NÞ(st 1)>0, та gcd(MÞ(st 1), NÞ(st 1))= gcd(MÞ(st), NÞ(st))=gcd(m, n).
Тепер можна скористуватися індуктивною гіпотезою для стану st 1, бо всі її засновки виконуються. Тому отримуємо, що MÞ(str)=NÞ(str)= gcd( MÞ(st 1), NÞ(st 1)).
З урахуванням того, що gcd(MÞ(st 1), NÞ(st 1))=gcd(m, n), маємо, що MÞ(str)=NÞ(str)=gcd(m, n).
Теорему доведено. ▄
Відзначимо дві обставини, пов’язані з теоремою коректності.
По-перше, теорему доведено при умові додатності значень змінних M та N. А як буде працювати програми, коли ця умова не виконується? Коли значення змінних M та N не є додатними та рівні між собою (наприклад, значення змінних M та N дорівнють –5), то програма зупиняється, не змінюючи стан. Але наявне від’ємне число (або 0), що є значенням змінних, не може вважатися їх найбільшим спільним дільником. Коли ж значення змінних різні і хоча б одне із значень є від’ємним або 0, то програма зациклюється. Отже, на правильний результат можна сподіватись лише для додатних значень змінних M та N.
По-друге, теорему коректності доведено при умові завершуваності програми. Така коректність називається частковою коректністю. Повна (тотальна) коректність програми P для певного класу ST вхідних даних означає, що програма є частково коректною та завершується на всіх вхідних даних з цього класу. Якщо позначити формулу завершуваності програми P на стані stÎST як termination(P)(st), а коректність – як correctness(P)(st), то умова часткової коректності задається формулою
"stÎST (termination(P)(st)Þcorrectness(P)(st),
а тотальної коректності –
"stÎST (termination(P)(st)Ùcorrectness(P)(st).
Теорема 1.4 (Про повну коректність програми GCD) Нехай стан st є такий, що MÞ(st)=m, NÞ(st)=n та m, n >0. Тоді для деякого стану str маємо, що sem_P(GCD)(st)¯=str та (MÞ(str))=(NÞ(str))=gcd(m, n).
Щоб отримати повну коректність програми для додатних значень змінних M та N, треба довести завершуваність програми (точніше, визначеність значення функції WH(p_g, f_g)(st)). Це означає, що треба довести визначеність значення NumItWH((p_g, f_g), st), якщо m, n >0.
Розглянемо послідовність станів змінних
st0=st, st1=f s(st0), st2=f s(st1), … .
Оскільки при обчисленні нових станів задіяна лише функція віднімання, яка є всюди визначеною, то кожен елемент послідовності є визначеним, а сама послідовність є нескінченною.
Доведемо, що в цій послідовності є стан, в якому значення змінних M та N співпадають. Доведення проведемо від супротивного. Нехай це не так, тобто нехай в цій послідовності для кожного стану значення M та N різні. Розглянемо тепер послідовність сум значень цих змінних, тобто послідовність
t 0=MÞ(st 0)+ NÞ(st 0), t 1=MÞ(st 1)+ NÞ(st 1), t 2=MÞ(st 2)+ NÞ(st 2), …
В початковому стані значення M та N додатні, тому t 0 >0. За відсутності рівних значень M та N додатними мають бути і всі інші числа t 0, t 1, t 2,… . Разом з тим послідовність є строго спадною, тобто t 0 > t 1 > t 2 >… , тому що нові значення M та N отримуються відніманням меншого з чисел від більшого. При наведених умовах послідовність t 0, t 1, t 2,… не може бути нескінченною, бо обмежена знизу числом 2, що є найменшою сумою двох додатних чисел.
Отримане протиріччя говорить про те, що в послідовності станів змінних st0=st, st1=f s(st0), st2=f s(st1), … є стан з однаковими значеннями M та N, на якому цикл зупиняється, тобто значення WH(p_g, f_g)(st) буде визначеним.
Це означає, що для додатних значень змінних M та N доведено повну коректність нашої програми. ▄
Зауваження 1.10 Звернемо ще раз увагу на те, що при доведенні теореми ми часом застосували програмістську термінологію, говорячи, наприклад, про ітерації циклу, про завершуваність програми, а не про обчислення послідовності певних значень функцій, як того вимагає композиційна семантика. Зроблено це для того, щоб доведення краще відповідало програмістській інтуїції. Втім, сподіваємось на те, що читач зуміє розпізнати та трансформувати програмістські терміни у точні математичні формулювання.
Варто підкреслити ще одну обставину, а саме, що без наявності формальної семантики та синтаксису ми не могли б навіть говорити про доведення різних властивостей програм, та зокрема, їх коректності. На інтуїтивному рівні розуміння програм може бути лише інтуїтивне обґрунтування властивостей програм.
Висновки
В цьому розділі був розглянутий простий приклад програми в мові SIPL. Ця мова є одним з варіантів простих мов подібного типу, наприклад, мови WHILE [Nilsons]. Фактично такі мови є мовами структурного програмування [Структурне програм]. Однак тут була дана композиційна семантика мови SIPL, яка базується на запропонованому В.Н. Редьком композиційному програмуванні [Редько]. Такім чином, основні результати цього розділу полягають у наступному:
1. Дано неформальний та формальний опис мови SIPL.
2. Для формального визначення синтаксису мови запропоновано її БНФ та розглянуті її властивості (дерева виводу, однозначність та неоднозначність БНФ).
3. Для формального визначення семантики мови побудовано алгебру даних мови SIPL та низку функціональних алгебр. Операціями цих алгебр є композиції, що формалізують засоби конструювання програм.
4. Визначено відображення побудови семантичного терму програми.
5. Досліджено низку тотожностей в алгебрі програм.
6. Продемонстрована можливість доведення часткової та повної коректності на підставі введених формалізацій.
Разом з тим виникає низка питань. Можливо, всі введені поняття і методи спрацьовують лише на простій мові, і для більш складних мов це не спрацює? Тобто чи є введені поняття необхідними та суттєвими, чи може вони випадкові? Які поняття ще слід ввести, щоб працювати з більш потужними мовами програмування?
Питання такого типу є загальнометодологічними питаннями. Їх розглянемо в наступному розділі.
Контрольні питання.
1. Які недоліки неформального опису мов програмування?
2. Яким чином задається синтаксис мови SIPL?
3. Що є деревом синтаксичного виводу програми?
4. Коли програма є синтаксично правильною?
5. Що таке неоднозначна БНФ?
6. Для чого вводиться пріоритет операцій?
7. Які пріоритети введено для операцій мови SIPL?
8. Які синтаксичні категорії та метазмінні введені в мові SIPL?
9. Які типи даних використовуються у мові SIPL?
10. Які алгебри даних пов’язані з мовою SIPL?
11. Як визначаються операції іменування та розіменування?
12. Які класу функцій використовуються для формалізації семантики мови SIPL?
13. Які типи номінативних функцій використовуються для формалізації семантики мови SIPL?
14. Як визначається суперпозиція в n-арну функцію?
15. Як визначається композиція присвоєння?
16. Як визначається композиція послідовного виконання?
17. Як визначається композиція розгалуження?
18. Як визначається композиція циклу?
19. Які програмні алгебри пов’язані з мовою SIPL?
20. За якими критеріями в перелік композицій включають функції?
21. Як визначається підалгебра алгебри A_Prog, породжена мовою SIPL?
22. Як частковість функцій впливає на визначення композицій?
23. Як визначається семантичний терм програми?
24. Як будується семантичний терм програми?
25. Які властивості виконуються для програмних алгебр?
26. Як визначаються монотонні функції?
27. Як визначаються еквітонні функції?
28. Які визначають програми мови SIPL?
29. Що таке часткова коректність програм?
30. Що таке повна коректність програм?
Вправи.
1. Довести однозначність синтаксичного аналізу при використанні правил пріоритету та асоціативності операцій.
2. Побудувати рекурентні співвідношення для визначення синтаксичних категорій.
3. Навести приклади неоднозначного аналізу програм мови SIPL.
4. Побудувати програми на мові SIPL для наступних задач (x,y, n – додатні цілі числа):
· обчислення x * y, використовуючи функції +, –,
· обчислення n!,
· обчислення x–y, використовуючи функцію віднімання одиниці (–1),
· перевірки парності числа n,
· обчислення x div y, використовуючи функції +, –,
· обчислення xy, використовуючи функції *,+, –,
· обчислення [lg n], використовуючи функції div, mod, +, –,
· обчислення x mod y, використовуючи функції +, –,
· обчислення 3x, використовуючи функції *,+, –,
5. Перевірити синтаксичну правильність програм, створених у вправі 4, побудувавши їх дерева синтаксичного виводу. Побудувати семантичні терми цих програм, та застосувати їх до певних вхідних даних.
6. Довести часткову та повну коректність програм, створених у вправі 4.
7. Довести лему про співпадіння дляпрограм мови SIPL, а саме, визначити за програмою мови SIPL змінні, від яких залежить програма (індукцією за структурою програми), та довести, що значення програми будуть однаковими на станах з однаковими значеннями таких змінних.
2. Розвиток основних понять програмування
Постійне розширення сфери застосування обчислювальної техніки і необхідність побудови все більш складних, але надійних програмних систем змушують дослідників знову і знову звертатися до визначення основних понять програмування. Незважаючи на різноманіття існуючих моделей програм і парадигм програмування, не можна не визнати тієї обставини, що розробка загальноприйнятної теорія програмування ще не завершена. Водночас зрозуміло, що центральною складової такої теорії повинні бути строгі уточнення понять програми і програмування. Одним із підходів до початкових уточнень цих понять є композиційно-номінативний підхід, який може розглядатися як подальший розвиток композиційного програмування.
Цей підхід базується на наступних трьох основних принципах: розвитку, композиційності і номінативності. Принцип розвитку (від абстрактного до конкретного) говорить про поступове уточнення поняття програми, починаючи з найбільш абстрактних і продовжуючи більш конкретними і багатими уточненнями. Принцип композиційності трактує програми як функції, що будуються з інших функцій за допомогою спеціальних операцій, які називаються композиціями. Принцип номінативності говорить про необхідність використовувати відношення іменування для роботи з програмами і даними.
Ідеї розвитку, композиційності і номінативності добре відомі і простежуються з глибокої давнини. Категорія розвитку є однієї з центральних категорій у такому філософському напрямку, як діалектика, серед представників якої виділимо Геракліта Ефеського та Г.В.Ф. Гегеля. Композиційні властивості мовних виразів були чітко сформульовані Г. Фреге та Р. Карнапом. Принцип композиційності був основним у композиційному програмуванні, запропонованому В.Н. Редьком. Різним аспектам номінативності (іменування) присвятили свої роботи Аристотель, Гоббс, Джон Стюарт Мілль, Джордж Буль, Пірс, Фреге, Рассел, Кріпке і багато інших.
Перш ніж переходити до детального розвитку основних понять програмування, проаналізуємо визначення поняття 'програма', наведені у словниках.
2.1 Аналіз словникових визначень поняття програми
Почнемо з визначень поняття програми, які наводяться у словниках і енциклопедіях. Великий тлумачний словник сучасної української мови[1], Меріам-Убстер Електронний словник[2] та інші словники дають наступне трактування слова 'програма'.
Етимологія: від грецького prographein – попередній запис (pro – перед + graphein – писати). Пізніше латинське programma: письмове повідомлення. Значення[3] :
· наперед продуманий план якої-небудь діяльності, роботи і т. ін.;
· план для програмування деякого механізму (як комп'ютер);
· послідовність кодів інструкцій, що можна ввести в механізм (наприклад, комп'ютер).
Аналізуючи це та інші визначення терміна 'програма', дійдемо висновку, що визначення використовують такі терміни, як 'план', 'послідовність', 'дія', 'інструкція', 'програмування', 'комп'ютер' і т.п. Подивимося, наприклад, на визначення першого терміна в цьому списку. 'План' є:
· креслення або діаграма,
· метод досягнення кінцевої мети,
· упорядкована класифікація частин проекту або мети,
· детальна програма дій.
Бачимо, що визначення терміна 'план', які нас цікавлять, звертаються знову до слова 'програма'. Звідси можна зробити два висновки:
1) словникові визначення поняття програми призводять до хибного кола, бо ніякого глибокого розвитку цього поняття не відбувається, а є лише досить проста тавтологія, коли фактичного розкриття терміну не відбувається, а стверджується, що програма – це те саме, що і план, а план є програмою,
2) поняття програми є дуже широким поняттям, яке не визначається як конкретизація деякого іншого поняття (не визначається за схемою родовидових понять Аристотеля).
Подібна ситуація буде і з іншими термінами з нашого списку. Правда, критикуючи словникові визначення за неповноту, зауважимо, що вони надають початкове уявлення про значення різних термінів. Тому треба погодитись зі словами М.Т. Рильського:
Не бійтесь заглядати у словник:
це пишний яр, а не сумне провалля.
Таким чином, термін 'програма' є надзвичайно загальним, багатоаспектним і не може бути простим способом визначений через інші терміни. Але як же тоді визначати такі загальні терміни?
Сформулювавши питання таким чином, ми фактично ставимо запитання про методи наукового пізнання і тим самим полишаємо область програмування і переходимо в більш загальну область, що називається гносеологією, або епістемологією, і яка визначається як наука про взаємини суб'єкта та об'єкта, про закони, форми і методи пізнання, а також відношенні знання до дійсності, критеріях його істинності і достовірності. Тут суб'єкт та об'єкт – філософські категорії: під суб'єктом розуміється той, хто досліджує об'єкт.
2.2 Розвиток поняття програми з гносеологічної точки зору
Насамперед необхідно обґрунтувати, що поняття програми дійсно є складним, багатоаспектним поняттям і не зводиться тривіальним чином до більш простих понять. Це стає зрозумілим, якщо згадати історію розвитку програм, що починалася з досить простих обчислювальних програм для перших комп'ютерів і потім поступово перетворилася в потужну галузь виробництва, яка залучає величезні людські і фінансові ресурси. Складність поняття програми зрозуміла і із словникових визначень. Уточнення таких складних, багатосторонніх та багатоаспектних понять має відбуватися згідно загальних законів гносеології. Сформулюємо приведене твердження у вигляді наступного принципу.
Принцип гносеологічності. Уточнення основних понять програмування здійснюється відповідно до загальних законів (принципів) гносеології, застосування яких має програмологічну спрямованість.
Наведений принцип має два аспекти. Перший стосується доцільності використання загальних законів (принципів) гносеології для уточнення основних понять програмування. Другий аспект говорить про те, що ці закони слід конкретизувати, орієнтуючись на предметну область, що досліджується, та на теорію, що будується, тобто на програмування та на програмологію. Тут під програмологією розуміється наука про програми та процеси програмування.
Гносеологія як наука про пізнання повинна, зокрема, надати нам загальні закони уточнення понять конкретних предметних областей. Складність використання гносеології з цією метою полягає в тому, що незважаючи на багатовікову історію її розвитку, все ж не створені загальноприйняті закони наукового пізнання. Існують різні школи і напрямки, що часто трактують одні і ті самі питання у різний спосіб. У силу цього для дослідника конкретної предметної області залишаються три можливості:
· приєднатися до однієї зі шкіл гносеології,
· розробити власний гносеологічний підхід,
· ігнорувати загальногносеологічні проблеми.
Кожна з можливостей має свої переваги та недоліки. Розробити власний підхід дуже складно. Це призведе до значних витрат на чисто філософську діяльність, займе багато часу. Ігнорування гносеологічних проблем призведе до примітивних помилок, які вже давно зрозумілі філософам. Тут є повна аналогія з теорією дебютів у шахах. Розробити власний дебют дуже важко, бо історія шахів нараховує тисячоліття і зроблено надзвичайно багато. Ігнорування теорії дебютів призведе до програшу вже на початку партії. Тому шахісти, як правило, використовують вже розроблені та досліджені дебюти. Так і ми спробуємо використати певний гносеологічний підхід. Але який? Звичайно той, що стоїть найближче до практики програмування.
Тому слід визначити ті особливості програмування, які повинні знайти своє обґрунтування в гносеологічному підході. Це перш за все програмування як поступове уточнення, програмування від абстрактного до конкретного. Це підтримується такими методами, як структурне, систематичне, об'єктно-орієнтоване програмування та таке інше. Виявляється, є гносеологічний підхід, який саме і проголошує метод розвитку (побудови від абстрактного до конкретного) своїм головним методом. Цей підхід називається діалектичною логікою.
Отже, в рамках даної роботи будемо спиратися саме на цей напрямок гносеології, який був розвинутий Г.В.Ф. Гегелем та його послідовниками. Правда, для наших цілей немає потреби використовувати діалектичну логіку у всій її потужності. Будемо використовувати лише ті елементи діалектичної логіки, які необхідні для опису понять програмування.
Основною складовою діалектичної логіки є система взаємопов'язаних та взаємообумовлених категорій, які тут розглядаються як всезагальні ознаки предметів. Прикладами категорій є категорії абстракне–конкретне, об’єктивне–суб’єктивне, якість–кількість–міра, елемент–частина–ціле, форма–зміст, явище–сутність, одиничне–особливе–всезагальне та багато інших.
Система категорій утворює каркас нашого мислення. Розбудова такої системи спирається на низку принципів.
Першим принципом є розвиток від абстрактного до конкретного: перехід від абстрактних, бідних за смислом визначень до конкретних, більш багатих за смислом. Другий принцип – це рух мислення від однієї категорії до протилежної за значенням з подальшим їх об’єднанням у третій категорії (тріадичний розвиток). Третій принцип фактично є певним уточненням перших двох принципів. Згідно йому категорії членуються на три групи, що відповідають трьом етапам пізнання. Перша група – це зовнішні визначення предметів, друга – внутрішні визначення, третя – визначення самого поняття. На першому етапі предмет визначається з боку його зовнішності, на другому визначається його внутрішня побудова та зв’язки з іншими предметами, на третьому поєднується зовнішні визначення предмета з його внутрішніми визначеннями.
Наведені етапи дослідження предмета часто формулюють у вигляді наступної схеми: синкретичний етап (предмет не членується на складові, розглядаються зовнішні відношення), аналітичний етап (розглядається внутрішня структура та відношення між складовими) та синтетичний етап (об’єднуються зовнішні та внутрішні відношення та складові.
Сформульовані принципи вказують на методи розбудови системи категорій. Та основний смисл прихований в самих категоріях. Виділяють біля сотні категорій, які всі пов’язані між собою. Таких зв’язків – тисячі. Тому немає простого викладу системи категорій. Проводячи аналогію з математикою, можемо казати, що визначення системи категорій задається складною системою з сотень рівнянь над сотнями змінних. Разом з тим для визначення основних понять програмування ми і не будемо використовувати усю потужність системи філософських категорій, а лише обмежимось тими моментами, які пов’язані з програмуванням. Цей висновок випливає і з принципу гносеологічності, але сформулюємо його як спеціальний принцип.
Принцип програмологічної проекції категорій: при визначенні основних понять програмування категорії розглядаються лише в тих аспектах, які відображають властивості програмування.
Зв’язки категорій часто формулюються як закони діалектики. Серед таких законів зупинимося більш докладно на законі заперечення заперечення. У діалектичній логіці заперечення розглядається як зміна (розвиток), що змінюючи річ (заперечуючи її), приводить до нової речі, яка зберігає в деякої іншій формі властивості початкової речі. Закон заперечення заперечення говорить про те, що зміна заперечує змінюване, результат у свою чергу змінюється новим запереченням, що приводить нас не до простого повторення початкового, а до його нового рівня розвитку. Тим самим цей закон стверджує спадкоємність, зв'язок нового зі старим, повторювальність на вищій стадії розвитку деяких властивостей нижчої стадії.
Нарешті, надамо певні пояснення категорії абстрактне–конкретне. Інколи ці терміни тлумачаться як уявне(ідеальне)–реальне. Тут ми беремо інше значення цих термінів. Абстрактне (походить від латинського abstraction – відволікання, виділення) означає одностороннє, просте, нерозвинуте. Конкретне (від латинського concretus – зрощене) означає єдність різних сторін, багатостороннє. Тут важливо відзначити, що конкретність розглядається саме як єдність, як системність.
Процес опису деякого предмета (речі, об'єкта) фіксується за допомогою понять. Як було сказано, розвиток понять будемо здійснювати від абстрактного до конкретного. Починаємо з найбільш абстрактних (але істотних) понять. Зміст понять задається за допомогою суджень, що розкривають властивості предмета. Сукупність суджень про поняття на визначеному етапі дослідження будемо називати рівнем абстракції, на якому розглядається поняття. На кожному рівні абстракції можна робити умовиводи, що формулюють властивості предмета дослідження. Крок конкретизації полягає в тому, що вводяться поняття і судження, які розкривають нові властивості предмета. На отриманому новому рівні абстракції робляться нові умовиводи і т.д.
Застосовуючи зазначені положення до програм, одержуємо наступний принцип.
Принцип розвитку (від абстрактного до конкретного). Програмні поняття уточнюється в процесі їх розвитку. Цей процес починається з найбільш абстрактних уявлень, які відображають загальні істотні властивості програм та програмування, потім поступово переходить до більш конкретних уявлень у їх єдності, які відображають специфічні властивості програм та програмування, і таким чином нарешті розкриває програмні поняття в їх багатстві та взаємозв'язках.
Слід відзначити, що наведений принцип (та і інші методологічні принципи та визначення) не слід тлумачити абсолютно. Зокрема, цей принцип безумовно слід розглядати в єдності з рухом пізнання від конкретного до абстрактного. Тому завжди треба брати до уваги відносність аспектів, переходи одних аспектів в інші, та пам’ятати в цілому про наявність складних взаємовідношень між поняттями. Сукупність таких відношень називають діалектикою понять.
Наведений принцип розвитку є дуже загальним, тому сформулюємо деякі наслідки, які розкривають його зміст. Насамперед відзначимо, що оскільки поняття будуть розглядатися на різних рівнях абстракції, то при їх вивченні варто чітко
· вказувати рівень абстракції, що розглядається (принцип фіксації рівня абстракції),
· при побудові умовиводів використовувати тільки такі властивості понять, що були явно визначені раніше (принцип достатньої підстави),
· не використовувати властивостей, заданих на інших рівнях і явно не визначених на рівні, що розглядається (принцип інкапсуляції рівнів абстракції),
· в процесі розвитку попередні властивості не відкидаються, а зберігаються на нових рівнях розвитку, можливо у іншій формі (принцип кумулятивності розвитку).
Ще одним наслідком принципу розвитку є принцип генетичності, який стверджує, що структури програм є похідними від їх генетичних структур (структур породження).
Підставою вибору того чи іншого напрямку розвитку є принцип єдності логічного і історичного. Цей принцип може розглядатися як певний варіант відомого гносеологічного принципа єдності теорії та практики.
Розвиток понять часто відбувається згідно тріаді розвитку: теза – антитеза – синтез.
Розглянемо простий приклад. Припустимо, що ми хочемо дати визначення терміну "теща" (теза). С цим терміном асоціюється інший термін – "зять" (антитеза). Наявність цих двох термінів (які протистоять один одному) ще не дає можливості безпосередньо визначити перший термін. Необхідно зробити ще один крок розвитку (синтез), що поєднає терміни "теща" та "зять". Це поєднання задається особою, що є дружиною зятя та дочкою тещі.
Наведений розвиток призвів до визначення терміну "теща", що приводиться у словниках: теща – мати дружини
Малюнок 2.1. Тріада розвитку
Підсумовуючи наведені вище гносеологічні положення, можна говорити про наступне.
1. Предмети світу пов’язані між собою. Це є емпіричний факт, що часто формулюється як принцип взаємозв’язку предметів (речей). Як наслідок отримуємо, що кожен предмет є єдністю багатьох сторін (аспектів).
2. Оскільки кожен предмет (крім дуже простих) має багато сторін, то неможливо визначити його одним визначенням.
3. Зважаючи на неможливість охопити всі сторони предмета одним визначенням, спочатку зупиняються лише на деяких аспектах (тобто предмет спочатку розглядається абстрактно).
4. Подальше визначення (уточнення) поняття предмета може відбуватися шляхом конкретизації обраних аспектів (як правило за родовидовою схемою Аристотеля), або (що є більш загальною схемою) за тріадою розвитку, коли далі обираються інші аспекти (тим самим вони є запереченням початковообраних аспектів), та які потім інтегруються з початковообраними аспектами.
5. Вибір аспектів визначається метою дослідження, але важливим є вибір суттєвих аспектів, що ведуть до визначення предмета по суті.
6. Цей вибір аспектів, як правило, відповідає наступній схемі: зовнішні аспекти – внутрішні аспекти – взаємозв’язок аспектів.
Озброївшись основними гносеологічними принципами, перейдемо до розгортання основних понять програмування.
2.3 Розвиток основних понять програмування
Для уточнення поняття програми будемо розглядати походження (генезис) тих понять, що виникають у процесі його розвитку. При цьому прагнемо, щоб нові поняття, які виникають були дуже простими і не вимагали для свого розуміння багатого досвіду програмування. У цьому сенсі запропоноване уточнення (експлікація) поняття програми може розглядатися як апріорна експлікація.
Звертаємо увагу на те, що термін 'поняття' буде вживатися в наступних смислах: 1) в інтуїтивному, коли поняття розглядається у всьому багатстві його властивостей, 2) у частково експлікованому, коли з поняттям зв'язуються тільки ті властивості, що визначені на фіксованому рівні абстракції. Будемо звертатися до інтуїтивного розуміння у тому випадку, коли необхідно ввести нову властивість, яка глибше розкриває зміст досліджуваного поняття. Частково експліковане розуміння використовується для вивчення властивостей поняття на фіксованому рівні абстракції. Сподіваємося, що з тексту завжди буде зрозуміло, про яке тлумачення йде мова.
Наша мета полягає в тому, щоб не просто ввести якісь визначення понять програмування, а продемонструвати їх зв’язки та те, як від одних понять ми мусимо переходити до інших.
Наприклад, ми хочемо визначити поняття університету. Перший аспект, що можна виділити (абстрагувати) в цьому понятті, це те, що університет складається із студентів. Але це дуже абстрактна характеристика університету. Переходимо до (діалектичного) заперечення цього аспекту: університет – це викладачі. Але знову таке визначення неповне. Далі ідемо до синтезу: університет це студенти та викладачі, пов’язані навчальним процесом (лекції, семінари, і таке інше). Це вже досить конкретне визначення. Але і така тріада є абстрактною. Під таке визначення університету підпадають і дитячий садок, і школа. Тому треба вводити ще більш конкретні визначення, розкриваючи структуру університету з різних сторін, (навчальні плані, факультети, приміщення і д. д. і т. п. Тільки на цьому шляху поняття університету буде розкрите конкретно, у його складових та їх зв’язках, призначенні університету та таке інше.
Така сама ситуація має місце і для понять програмування. Розглянемо ще один простий приклад. Припустимо, що містер NN хоче дізнатися про стан свого банківського рахунку. Він зв'язується з банківським службовцем, для якого проблема містера NN перестає бути одиничною проблемою, а стає масовою: як за номером банківського рахунку з'ясувати стан рахунку. Для розв'язання цієї проблеми службовець використовує спеціальну програму. Але ця програма є однієї з багатьох програм, таких як системи керування базами даних, операційні системи і т.п., які розробляються і обслуговуються програмістами банку. Цей приклад показує як, починаючи з "маленької" індивідуальної проблеми, ми змушені переходити до все більш загальних проблем, які вимагають для свого розв’язання усе більш складних і розвинених програмних систем. Приблизно таким же способом будемо розвивати поняття програми, починаючи з найбільш простих абстрактних властивостей і продовжуючи більш спеціальними і багатими властивостями. Отже, процес розвитку веде нас від індивідуальних властивостей через особливі до загальних.
Як уже відзначалось раніше, у процесі уточнення програмних понять будемо часто використовувати тріаду розвитку: теза – антитеза – синтез.
Уточнення поняття програми природно починати, як говорили древні, ab ovo – із самого початку.
Але що обрати за початок?
Можна починати від понять програми та програмування. Але наведені приклади говорять про те, що для уточнення цих понять все одно необхідно вийти на всезагальні поняття. Такою всезагальністю є поняття людства (суспільства). З цього і почнемо розвиток понять програмування.
2.3.1 Початкова тріада понять програмування
При пізнанні сутності програм та програмування ми повинні в першу виходити з єдності трьох визначень їх понять: одиничності, особливості та всезагальності. Цим категоріям відповідають такі моменти розгляду досліджуваного предмету, як елемент, частина та ціле. Зрозуміло, що сфера програмування належить до такої цілісності, як людство (суспільство). Але це занадто багата цілісність. Вона містить такі особливості, як сфери освіти, охорони здоров’я, оборони та таке інше. Серед цих особливих сфер є і сфера діяльності, яка пов’язана з програмами та програмуванням. Назвемо цю сферу сферою інформатизації (це занадто широко, але і більш вузький термін важко вказати). Тому згідно принципу програмологічної проекції будемо як всезагальне для теорії програмування брати цю сферу (малюнок 2.2).
Дата добавления: 2019-02-13; просмотров: 289; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!