Побудова семантичного терму програми
Програма мови SIPL може бути перетворена в семантичний терм (терм програмної алгебри), який задає семантику цієї програми (семантичну функцію програми), перетвореннями такого типу:
· sem_P: Prog ® FS
· sem_S: Stm ® FS
· sem_A: Aexp ® FA
· sem_B: Bexp ® FB
Ці перетворення задаються рекурсивно (за структурою програми). Тому побудова семантичного терму залежить від вибору структури синтаксичного запису програми. Тут треба зважати на неоднозначність обраної нами граматики, що може призвести до різної семантики програм. Для досягненя однозначності треба користуватись пріоритетами операцій та типом їх асоціативності.
Таблиця 1.6
| Правило заміни | Номер правила |
|
sem_P: Prog ® FS задається правилами:
| |
| sem_P(beginSend)= sem_S(S) | NS_Prog |
|
sem_S: Stm ® FS задається правилами:
| |
| sem_S(x:=a)=ASx(sem_A(a)) sem_S(S1;S2)= sem_S(S1) ·sem_S(S2) sem_S(ifbthenS1elseS2)= IF(sem_B(b), sem_S(S1), sem_S(S2)) sem_S(whilebdoS)= WH(sem_B(b), sem_S(S)) sem_S(beginSend)=(sem_S(S)) sem_S(skip)=id | NS_Stm_As NS_Stm_Seq NS_Stm_If NS_Stm_Wh NS_Stm_skip |
|
sem_A: Aexp ® FA задається правилами:
| |
sem_A(n))= 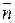 sem_A(x))=xÞ
sem_A(a1+a2)=S2(add, sem_A(a1), sem_A(a2))
sem_A(a1–a2)=S2(sub, sem_A(a1), sem_A(a2))
sem_A(a1*a2)=S2(mult, sem_A(a1), sem_A(a2))
sem_A(a1¸a2)=S2(div, sem_A(a1), sem_A(a2))
sem_A((a))=sem_A(a)
sem_A(x))=xÞ
sem_A(a1+a2)=S2(add, sem_A(a1), sem_A(a2))
sem_A(a1–a2)=S2(sub, sem_A(a1), sem_A(a2))
sem_A(a1*a2)=S2(mult, sem_A(a1), sem_A(a2))
sem_A(a1¸a2)=S2(div, sem_A(a1), sem_A(a2))
sem_A((a))=sem_A(a)
| NS_A_N um NS_A_VarNS_A_Add NS_A_Sub NS_A_Mult NS_A_D iv NS_A_Par |
|
sem_B: Bexp ® FB задається правилами:
| |
sem_B(true)=  sem_B(false)=
sem_B(false)= 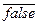 sem_B(a1<a2)=S2(less, sem_A(a1), sem_A(a2))
sem_B(a1£a2)=S2(leq, sem_A(a1), sem_A(a2))
sem_B(a1=a2)=S2(eq, sem_A(a1), sem_A(a2))
sem_B(a1¹a2)=S2(neq, sem_A(a1), sem_A(a2))
sem_B(a1³a2)=S2(geq, sem_A(a1), sem_A(a2))
sem_B(a1>a2)=S2(gr, sem_A(a1), sem_A(a2))
sem_B(b1Úb2)=S2(or, sem_B(b1), sem_B(b2))
sem_B(b1Ùb2)=S2(and, sem_B(b1), sem_B(b2))
sem_B(Øb)=S1(neg, sem_B(b))
sem_B((b))= sem_B(b)
sem_B(a1<a2)=S2(less, sem_A(a1), sem_A(a2))
sem_B(a1£a2)=S2(leq, sem_A(a1), sem_A(a2))
sem_B(a1=a2)=S2(eq, sem_A(a1), sem_A(a2))
sem_B(a1¹a2)=S2(neq, sem_A(a1), sem_A(a2))
sem_B(a1³a2)=S2(geq, sem_A(a1), sem_A(a2))
sem_B(a1>a2)=S2(gr, sem_A(a1), sem_A(a2))
sem_B(b1Úb2)=S2(or, sem_B(b1), sem_B(b2))
sem_B(b1Ùb2)=S2(and, sem_B(b1), sem_B(b2))
sem_B(Øb)=S1(neg, sem_B(b))
sem_B((b))= sem_B(b)
| NS_B_true NS_B_false NS_B_less NS_B_leq NS_B_eq NS_B_neq NS_B_geq NS_B_gr NS_B_or NS_B_and NS_B_neg NS_B_Par |
|
|
|
Наведені правила слід розглядати як загальні правила, які в логіці називають схемами правил. Щоб із загального правила (метаправила) отримати конкретне правило (об’єктне правило), слід замість синтаксичних метасимволів, таких як a, b, S, P, n, x, підставити конкретні синтаксичні елементи (записи), наприклад замість a підставити N–M, замість b – M>N і т.п. Далі ліва частина конкретного правила заміняються на його праву частину і т.д.
Приклад 1.2 Побудуємо семантичний терм виразу X+Y*Z. Побудова терму полягає в обчисленні значення sem_A(X+Y*Z). Щоб зробити перший крок такого обчислення, треба віднайти правило, ліва частина якого буде співпадати з записом sem_A(X+Y*Z) при відповідній конкретизації такого правила. Цей процес називається уніфікацією двох записів (термів). В нашому випадку можлива уніфікація з лівою частиною правил NS_A_Add та NS_A_Mult. В першому випадку уніфікація sem_A(X+Y*Z) та sem_A(a1+a2) можлива при заміні a1 на X та a2 на Y*Z, а в другому уніфікація sem_A(X+Y*Z) та sem_A(a1*a2) можлива при заміні a1 на X+Y та a2 на Z. Наведені заміни називаються уніфікаторами і зазвичай позначаються [a1/X, a2 /Y*Z] та [a1/X+Y, a2 /Z], або [a1aX, a2 aY*Z] та [a1aX+Y, a2 aZ]. Зазначимо, що друга уніфікація порушує пріоритет операцій, тому розглядаємо лише першу уніфікацію. Застосування цієї уніфікації до правила NS_A_Add призводить до наступного конкретного (об’єктного) правила
|
|
|
NS_A_Add¢: sem_A(X+Y*Z)= S2(add, sem_A(X), sem_A(Y*Z)).
Застосування цього правила дозволяє перетворити запис sem_A(X+Y*Z) в запис S2(add, sem_A(X), sem_A(Y*Z)). Цей запис містить два підзаписи (sem_A(X) та sem_A(Y*Z)), до яких можна застосувати перетворення. А саме, підзапис sem_A(X) уніфікується з лівою частиною правила NS_A_Var за допомогою уніфікатора [x/X], а підзапис sem_A(Y*Z) – з NS_A_Mult за допомогою уніфікатора [a1/Y, a2/Z]. Застосування цих уніфікаторів призводить до двох нових конкретних правил
NS_A_Var¢: sem_A(X)= XÞ та
NS_A_Mult¢: sem_A(Y*Z)= S2(mult, sem_A(Y), sem_A(Z)).
Застосовуючи ці правила до виразу S2(add, sem_A(X), sem_A(Y*Z)) отримаємо S2(add, XÞ, S2(mult, sem_A(Y), sem_A(Z))). Залишилось конкретизувати правило NS_A_Var, щоб отримати остаточний результат
sem_A(X+Y*Z)= S2(add, XÞ, S2(mult, YÞ, ZÞ))▄
Отже, процес побудови семантичного терму програми полягає в послідовному перетворенні запису, для якого будується семантичний терм. Ці перетворення вимагають наступних дій:
|
|
|
· вибір загального правила, яке можна застосувати до підзапису поточного виразу з урахуванням пріоритету операцій,
· уніфікація лівої частини правила з обраним підзаписом,
· отримання конкретного правила із загального правила,
· заміна у поточному записі лівої частини конкретного правила на його праву частину.
Більш формально процес перетворень такого типу сформульований в теорії переписуючих правил.
Зауважимо ще раз, що ми тлумачимо відображення sem_P: Prog ® FS, sem_S: Stm ® FS, sem_A: Aexp ® FA, sem_B: Bexp ® FB синкретично, вважаючи в залежності від контексту, що це відображення в відповідні функції класів FS, FA, FB, або в терми, що задають функції відповідних класів.
Приклад 1.3 Побудовати семантичний терм програми SIPL. Побудову будемо робити згідно вищенаведених правил. Деталі не вказуємо.
sem_P(GCD)=
= sem_P(begin
while M¹N do
if M>N then M:=M–N else N:=N–M
end)=
= sem_S(while M¹N do if M>N then M:=M–N else N:=N–M)=
= WH(sem_B(M¹N), sem_S(if M>N then M:=M–N else N:=N–M))=
= WH(S2(neq, sem_A(M), sem_A(N)),
IF(sem_B(M>N), sem_S(M:=M–N), sem_S(N:=N–M)))=
= WH(S2(neq, MÞ, NÞ), IF(S2(gr,MÞ,NÞ),
AS M(sem_A(M–N)), AS N(sem_A(N–M))))=
= WH(S2(neq, MÞ, NÞ), IF(S2(gr,MÞ,NÞ),
AS M(S2(sub,sem_A(M),sem_A(N))), AS N(S2(sub,sem_A(N),sem_A(M)))))=
=WH(S2(neq, MÞ, NÞ),
|
|
|
IF(S2(gr, MÞ, NÞ),
ASM( S2(sub, MÞ, NÞ)),
ASN( S2(sub, NÞ, MÞ))))▄
Повернемось тепер до доведення того факту, що семантика довільної програми мови SIPL задається термом алгебри A _ SIPL. Дійсно, аналізуючи таблицю 1.6 бачимо, що там фігурують лише базові фукції алгебри A _ SIPL. Більш стоге доведення можна отримати індукцією за структурою програми SIPL. Таким чином, є справедливим наступне твердження.
Теорема 1.1. Длядовільної програми мови SIPL її семантична функція задається термом алгебри A _ SIPL.
Дата добавления: 2019-02-13; просмотров: 253; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
