Правила дифференцирования функций.

Пусть U(х) и V(х) дифференцируемы в точке х.

1. (U(x) + V(x))` = U`(x) + V`(x)

2. (U(x) * V(x))` = U`(x) * V`(x) + V`(x) * U`(x)

3. (C*U(x))` = CU`(x), C - const

4. (U(x) / V(x))` = [U`(x) * V(x) - V`(x) * U(x)]/ V²(x)

Таблица производных.

1. C` = 0, C – const.

2. x` = 1

3. (x^α)` = α x^{α – 1}, α Є R

4. (a^x)` = a^x lnx, a>0 , a≠1

5. (ln x)` = 1/x

6. (sin x)` = cos x

7. (cos x)` = - sin x

8. (tg x)` = 1/(cos x)²

9. (ctg x)` = - 1/(sin x)²

10. (arcsin x)` = 1/ ²)

11. (arccos x)` = - 1/ 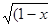²)

12. (arctg x)` = 1/(1 + x²)

13. (arcctg x)` = - [1/(1 + x²)]

правила для нахождения дифференциала можно написать самим, умножив соответствующее правило взятия производной на dx.

Например: d sinx = (sinx)`dx = cosx dx.

Пример 1. Найти приращение функции f(x) = x², если х = 1, ∆х = 0,1

Решение: f(х) = х², f(х+∆х) = (х+∆х)²

Найдем приращение функции ∆f = f(x+∆x) – f(x) = (x+∆x)² – x² = x²+2x*∆x+∆x² – x² = 2x*∆x + ∆x²/

Подставим значения х=1 и ∆х= 0,1, получим ∆f = 2*1*0,1 + (0,1)² = 0,2+0,01 = 0,21

Пример 2. Найти производную функции f(x) = x², в произвольной точке х по определению производной, т.е. не используя таблицу производных.

∆x→0

Решение: (х²)` = lim ∆f / ∆х

Из первого примера ∆f = 2x*∆x+∆x², подставим, получим

∆x→0

∆x→0

∆x→0

(x²)` = lim ∆f / ∆х = lim (2x*∆x+∆x²)/∆x = lim  [∆x (2х + ∆х)]/ ∆x = 2x

 

Пример 3. у = 1-х, Найти ∆у при х=2, ∆ = 0,1

Решение: у(х) = 1-х, у(х+∆х) = 1 – (х+∆х),

∆у = у (х+∆х) – у(х) = 1-х - ∆х – (1 – х) = 1-х - ∆х – 1 + х = - ∆х

при х = 2, ∆х = 0,1 ∆у = -∆х = -0,1.

Пример 4. Найти производную от функции у=3х⁴ – 2х² + 1.

Решение у` = 3*4х³ – 2*2х + 0 = 12х³ – 4х.

Пример 5. Найти производную от функции у = x² *℮^х.

Решение: у` = (x<sup>2</sup>)` *℮^х + x² *(℮^х)` = 2x ℮^х + x² *℮^х ln℮

ln ℮ = log_℮℮ = 1.         y` = 2x℮^x + x² * ℮^x

Пример 6. У = х/(х²+1). Найти у`.

Решение у` = [1*(х²+1) – х*2х] / (х²+1)² = [х²+1 – 2х²] / (x² +1)² = (1-x²) / (x²+1)²

Производные от сложных функций.

Формула для нахождения производной от сложной функции такова:

[f (φ(х))]` = f<sub>φ</sub>`(φ(x)) * φ`(x)

Например: у = (1-х²)³; у`= 3(1 –х<sup>2</sup>)<sup>2</sup> * (-2х) или у = sin<sup>2</sup>х; у` = 2sinx * cosx. 

Пример 7 . Найти dy, если у = sin 3х

Решение dy = у` * dx = (sin3x)` dx = (cos3x) * 3dx = 3 cos3x dx.

Пример 8. Найти dy, если у = 2^{х^2}/

Решение: dy = y` * dx = (2<sup>x^2</sup>)` * dx = 2^{x^2} ln2 * 2xdx

 

Производные высших порядков.

Пусть мы нашли от функции у = f(х) ее производную у` = f `(х). Производная от этой производной и называется производной второго порядка от функции f(х) и обозначается у`` или f `` (х) или (d²y) / (dx²). Аналогично определяются и обозначаются:         производная третьего порядка у``` = f ```(x) = (d³y) / (dx³).

                         производная четвертого порядка у^IV = f ^IV(x) = (d⁴y) / (dx⁴).

                         производная n-oго порядка у⁽ⁿ⁾ = f ⁽ⁿ⁾(x) = (d ⁿ y) / (dxⁿ).

Пример: у = 5х⁴ – 3х³ + 2х – 2. Найти у``.

Решение. Находим в начале первую производную: у` = 20х³ – 9х² +2, потом вторую от первой производной: у`` = 60х² – 18х.

Пример. y=хsinx. Найти у```.

Решение. y` = sinx + xcosx

y`` = cosx + cosx – x sinx = 2cosx – x sinx

y``` = -2sinx – sinx – x cosx = -3sinx – x cosx.

Тема 12. Понятие первообразной. Неопределенный интеграл. Свойства неопределенного интеграла.

Определение. Функция F(x) называется первообразной для функции f(x) на интервале Х, если в каждой точке этого интервала выполняется условие

F ` (x)=f(x).

Например, для функции f(x) = 2х первообразной является F(х) = х² для любых х Є (-∞, ∞).

Действительно, F`(x) = 2x = f(x).

F₁(x) = x² + 2 так же является первообразной для f(x) = 2x, F₂(x) = x² – 100 первообразная той же функции f(x) = 2x.

Теорема. Если F₁(x) и F₂(x) первообразные для функции f(x) на некотором интервале Х, то найдется такое число С, что справедливо равенство:

F₂(x) = F₁(x) + C,

Или можно сказать так, две первообразные для одной и той же функции отличаются друг от друга на постоянное слагаемое.

Определение. Совокупность всех первообразных для функции f(x) на интервале Х называется неопределенным интегралом от функции f(x) и обозначается 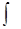f(x)dx, где 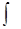- знак интеграла, f(x) – подинтегральная функция, f(x)dx – подинтегральное выражение. Таким образом

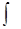f(x)dx = F(x) + C,

F(x) – некоторая первообразная для f(x), С – произвольная постоянная. Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

---

Дата добавления: 2019-02-12; просмотров: 181; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!