Завдання про проведення профілактичних робіт

МЕТОДИ стохастичного програмування

Проблема вибору рішення в умовах ризику та невизначеності.

Оптимізаційні задачі та їх математичні моделі в припущенні, що вся вихідна інформація однозначно задана, називаються детермінованими. У дійсності ж детерміновані моделі часто неадекватні реальним процесам, оскільки в практичних завданнях буває важко визначити точні значення параметрів моделі. Це пояснюється неповнотою і неточністю даних, на основі яких формується модель. Наявність невизначених факторів переводить задачу в нову якість: вона з задачі знаходження оптимального рішення перетворюється в задачу вибору рішення в умовах неповної інформації та невизначеності, що забезпечує по можливості максимальне значення показника ефективності.

У деяких випадках параметри носять імовірнісний характер і являють собою випадкові величини, характеристики яких нам відомі або в принципі можуть бути отримані. Оптимізаційні задачі, в яких окремі або всі параметри є випадковими величинами, називаються стохастичними. Обмеженість і неточність інформації про завдання призводить до ситуації, в якій доводиться приймати рішення в умовах ризику. Теорія і методи вирішення екстремальних задач в умовах неповної інформації вивчається в розділі стохастичного програмування. В інших випадках наявна інформація не дозволяє скласти уявлення про характер зміни параметрів математичної моделі і не має сенсу говорити про їх законах розподілу або інших імовірнісних характеристиках. У таких ситуаціях доводиться приймати рішення в стані невизначеності. З точки зору вихідних даних задачі стохастичного програмування є проміжними між оптимізаційними завданнями, поставленими в умовах повної визначеності і в умовах невизначеності.

Основою для побудови всіх моделей стохастичного програмування служить перетворення вихідної задачі в імовірнісної постановці в еквівалентну задачу, що володіє детермінованою структурою. У стохастичному програмуванні досліджуються одно крокові і багатокрокові завдання. Завдання, в яких рішення вибирається один раз і воно не змінюється при надходженні інформації про реалізаціях випадкових параметрів, називаються одно крокових. У завданнях цього класу цільова функція і обмеження можуть бути обрані різними способами. В якості цільової функції можуть бути прийняті: - математичне сподівання деякої функції від рішення, - комбінація математичного сподівання і середнього квадратичного відхилення, - ймовірність попадання функції від вирішення в деяку область.

Обмеження задачі в одних випадках можуть виконуватися при всіх можливих значеннях випадкових параметрів (жорстка постановка), а в інших випадках потрібна, щоб вірогідність попадання рішення в допустиму область була не менше заданої (модель з імовірнісними обмеженнями). У кожній конкретній задачі доводиться спеціально обумовлювати, що розуміється під допустимим і оптимальним рішеннями. У багатокрокових задачах по мірі отримання додаткової інформації про розвиток процесу є можливість неодноразової коректування рішень, прийнятих раніше. Природно, що для потреб практики багатокрокові завдання більш кращі, ніж одно крокові. Їхнє дослідження, взагалі кажучи, представляє більш складну задачу, і тут не розглядаються.

Завдання стохастичного програмування з випадковими параметрами в цільової функції

Розглянемо задачі стохастичного програмування, в яких випадкові параметри містяться тільки в цільовій функції. Нехтуючи випадковістю ряду параметрів і замінюючи їх середніми значеннями, такі завдання часто зводяться до звичайних детермінованим завданням. Як правило, така заміна може бути здійснена, якщо випадкові параметри мало відрізняються від своїх математичних сподівань, однак, якщо вплив випадковості на цікавий для нас процес істотно, то буде необачно використовувати даний критерій. Оптимізація «в середньому» буде законною, якщо процес має властивість повторюваності і недолік показника ефективності в одних випадках компенсується його надлишком в інших. Використання критерію середнього значення припускає можливість багаторазового вирішення однієї і тієї ж задачі, поки не будуть отримані досить точні розрахункові формули.

Нехай х - випадкова величина з математичним очікуванням m і дисперсією σ². Якщо (x₁, x₂, ... , x _n) - випадкова вибірка об'єму n, то вибіркове середнє 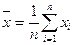має дисперсію σ²/n. Тому при n→ ∞ σ²/n → 0, і означає 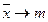по ймовірності. Іншими словами, при достатньо великому обсязі вибірки різниця між вибірковим середнім та математичним очікуванням прагне до нуля. Отже, використання критерію середнього значення допустимо лише у випадку, коли одне й те саме рішення доводиться приймати велику кількість разів. Навпаки, якщо необхідність у прийнятті деякого рішення зустрічається рідко, то середнє значення може значно відрізнятися від математичного очікування, і орієнтація на середнє значення буде приводити до невірних результатів для рішень, які доводиться приймати невелике число раз. Це означає доцільність введення критерію, в якому враховується не тільки середнє значення, але також розкид можливих значень відносно середнього, тобто дисперсія або середнє квадратичне відхилення. Можливим критерієм, що відповідає цій меті, є комбінація математичного сподівання і середнього квадратичного відхилення.

Завдання про проведення профілактичних робіт

В процесі експлуатації верстата можуть виникати несправності, і верстат зупиняється для їх усунення. Час усунення несправності постійно й дорівнює Т _В₁ Після ремонту верстат знову включається і продовжує свою роботу. Припустимо, що протягом часу t верстат n(t) раз виходить з ладу, і нехай ця величина має порядок n(t) = at^α, де а – випадкова величина з математичним очікуванням m = М(а) і середнім квадратичним відхиленням σ = σ(а). Показник α > 1, так як з плином часу верстат виробляє свій ресурс, і його надійність зменшується (значення α = 1 означає, що відмови верстата зростають пропорційно часу і «старіння» не відбувається). Через певний час проводиться профілактика верстата, триваюча час Т _В₂, і він відновлює усі свої характеристики надійності до первісного стану. Потрібно визначити оптимальний час між сусідніми профілактиками, при якому коефіцієнт простою К _П верстата був би мінімальним. Під коефіцієнтом простою буєм розуміти частку часу, протягом якого верстат не працює.

Протягом періоду тривалості t верстат простоює час 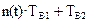, і, отже, коефіцієнт простою верстата дорівнює

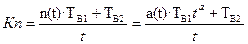(13)

Завдання мінімізації функції (13) є задачею стохастичного програмування, оскільки параметр α випадковий. Для вирішення завдання застосовні два критерії, що дозволяють звести задачу до детермінованої: критерій середнього значення і комбінований критерій середнього значення і середнього квадратичного відхилення. Згідно з першим критерієм в якості цільової функції береться математичне очікування коефіцієнта простою, тобто

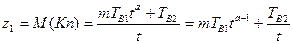
Оптимальне рішення 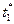знаходиться з рівняння уравнения 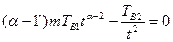або 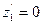, звідси

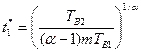(14)

Згідно комбінованому критерію в якості цільової функції береться 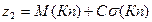, где С – задана постійна, визначальна «ступінь важливості» середнього квадратичного відхилення по відношенню до математичного сподівання. Так як Так как , то

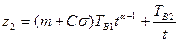
Як і у випадку першого критерію знаходимо оптимальний час між профілактики

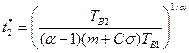
Приклад 6. У задачі про проведення профілактичних робіт приймемо наступні дані 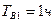, , 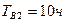, , 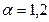, 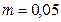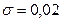С=1. Тоді у відповідності з формулами (14) і (15) отримаємо 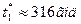, 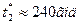. Таким чином, оптимальний час між профілактики залежить від обраного критерію, і якщо таких верстатів багато, то доцільно проводити профілактику через 316 год, а при малому числі верстатів час між проведенням профілактики слід скоротити до 240 год.

Дата добавления: 2019-02-12; просмотров: 131; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!