Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.

det A ¹ 0;

Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.

Теорема. Система из n уравнений с n неизвестными

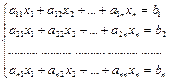
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

x_i = D _i / D , где

D = det A , а D _i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i .

D _i =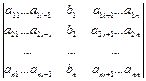

      

При D = 0 система имеет бесконечное множество решений.

Решение систем линейных уравнений матричным методом.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Метод удобен для решения систем невысокого порядка.

Метод основан на применении обратной матрицы.

Пусть дана система уравнений :

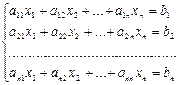
Составим матрицы: A = 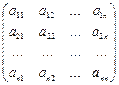;    B = ;     X = .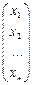

Систему уравнений можно записать:

A × X = B .

Сделаем следующее преобразование: A ^-1 × A × X = A ^-1 × B ,

т.к. А^-1 × А = Е, то Е × Х = А^-1 × В

Х = А^-1 × В

Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.

       Пример. Решить систему уравнений:

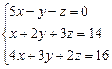
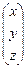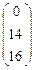Х = , B = , A =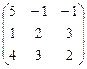

Найдем обратную матрицу А^-1.

D = det A = 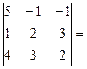5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.

M ₁₁ =  = -5;         M ₂₁ = 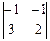 = 1;              M ₃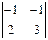₁ =    = -1;

M ₁₂ = 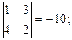           M ₂₂ =  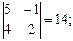               M ₃₂ =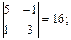

M ₁₃ = 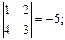             M ₂₃ =  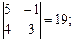               M ₃₃ =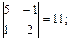

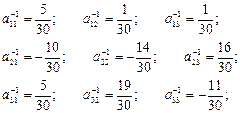                A ^-1 = ;

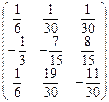Находим матрицу Х.

Х = 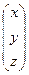= А^-1В = × = .

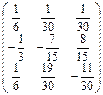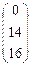Итого решения системы: x =1; y = 2; z = 3.

Метод Гаусса. Однородные системы линейных уравнений и их решение.

Метод Гаусса.

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

       Рассмотрим систему линейных уравнений:

 

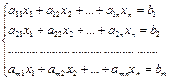
       Разделим обе части 1–го уравнения на a ₁₁ ¹ 0, затем:

1) умножим на а₂₁ и вычтем из второго уравнения

2) умножим на а₃₁ и вычтем из третьего уравнения

И т.д.

Получим:

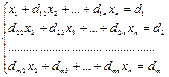, где d _{1 j} = a _{1 j} / a ₁₁ , j = 2, 3, …, n +1.

d_ij = a_ij – a_i1d_1j    i = 2, 3, … , n;  j = 2, 3, … , n+1.

Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.

3 вывода: 1. решение одно

Система несовместна

Решений бесчисленное множество

Однородные системы линейных уравнений

Если правая часть каждого уравнения в системе линейных уравнений нулевая, то система называется однородной.

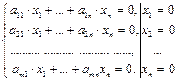
Однородная система всегда совместна, т.к. имеет нулевое решение. Это решение называется тривиальным.

Теорема. Для того, чтобы однородная система 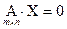 имела нулевое решение необходимо и достаточно, чтобы ранг матрицы был меньше числа неизвестных.

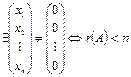
Следствие. Однородная система с матрицей 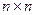 имеет ненулевое решение тогда и только тогда, когда определитель системы равен 0.

Некоторые свойства решений однородных систем:

· Если набор неизвестных – решение однородной системы, то коэффициент любой также является решением.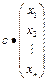  

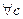
· Есл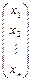и и 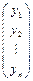 какие-то решения однородной системы, то +  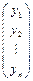- также является решением этой системы.

---

Дата добавления: 2019-02-12; просмотров: 209; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!