Поверхностные интегралы 1 рода
Формула из теории: 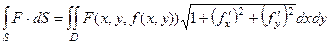 .
.
Задача 10. Найти поверхностный интеграл 1-го рода от скалярной функции 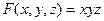 по треугольнику с вершинами (1,0,0), (0,1,0) и (0,0,1).
по треугольнику с вершинами (1,0,0), (0,1,0) и (0,0,1).
Решение. Во-первых, нужно получить явное уравнение плоскости, в которой расположен треугольник. Пусть 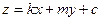 . Подставим точку (0,0,1), получим
. Подставим точку (0,0,1), получим 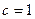 .
.
Подставим (1,0,0), получим 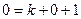 , откуда
, откуда 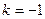 .
.
Подставим (0,1,0), получим 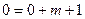 , откуда
, откуда 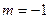 .
.
Итак, уравнение плоскости: 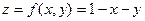 .
.
Тогда 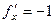 ,
, 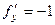 .
.
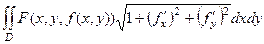 =
= 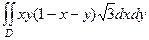 , где
, где  - проекция исходного треугольника на плоскость, т.е. треугольник с вершинами (0,0), (1,0) и (0,1) в плоскости, ограниченный сверху линией
- проекция исходного треугольника на плоскость, т.е. треугольник с вершинами (0,0), (1,0) и (0,1) в плоскости, ограниченный сверху линией 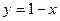 .
.

Расстановка пределов в таком двойном интеграле была подробно изучена в прошлом семестре:
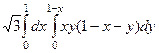 =
= 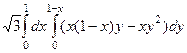 =
=
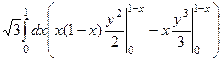 =
=
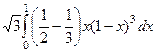 =
= 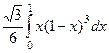 . Далее, чтобы уменьшить количество арифметических действий при раскрытии скобок, можно сделать замену
. Далее, чтобы уменьшить количество арифметических действий при раскрытии скобок, можно сделать замену
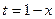 , при этом получим
, при этом получим 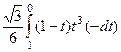 =
= 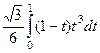 =
=
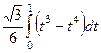 =
= 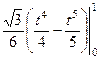 =
= 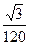 . Ответ.
. Ответ. 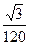 .
.
Задача 10. Найти поверхностный интеграл 1-го рода от скалярной функции 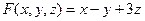 по полусфере радиуса 3 в верхней полуплоскости.
по полусфере радиуса 3 в верхней полуплоскости.
Решение. Уравнение сферы 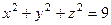 , тогда явное уравнение данной полусферы
, тогда явное уравнение данной полусферы 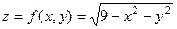 , соответственно
, соответственно
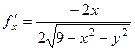 ,
, 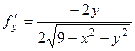 .
.
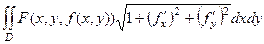 =
=
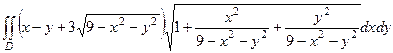 =
=
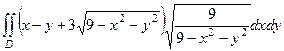 , где
, где  - проекция этой полусферы на плоскость Оху т.е. круг радиуса 3:
- проекция этой полусферы на плоскость Оху т.е. круг радиуса 3: 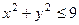 .
.
Разобьём на 2 слагаемых, причём во 2-м корни сокращаются:
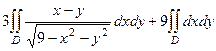 . В первом перейдём к полярным координатам, а во втором интеграл от 1, т.е. это просто площадь круга.
. В первом перейдём к полярным координатам, а во втором интеграл от 1, т.е. это просто площадь круга.
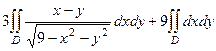 =
= 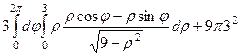 =
= 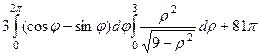 =
=
= 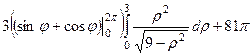 =
= 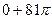 =
= 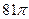 .
.
интеграл по 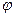 получается 0, поэтому в первом слагаемом интеграл по
получается 0, поэтому в первом слагаемом интеграл по 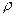 вычислять уже не нужно.
вычислять уже не нужно.
Ответ. 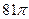 .
.
|
|
|
Криволинейные интегралы 2 рода
Задача 12.
Найти работу векторного поля 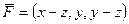 по перемещению точки по винтовой линии (спирали), заданной уравнениями
по перемещению точки по винтовой линии (спирали), заданной уравнениями
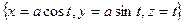 ,
, 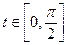 .
.
Решение. Требуется вычислить такой интеграл:
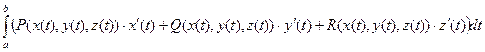
или его краткий вид: 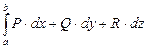 .
.
Производные: 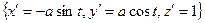 .
.
Тогда
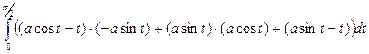 =
=
Заметим, что 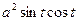 присутствует со знаками + и –, сокращается.
присутствует со знаками + и –, сокращается.
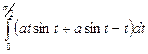 =
= 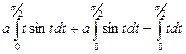 , в первом из них применим интегрирование по частям:
, в первом из них применим интегрирование по частям: 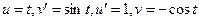 .
.
 =
=
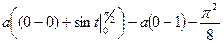 =
= 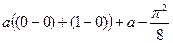 =
= 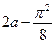 .
.
Ответ. 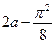 .
.
Вариант этой задачи для 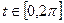 (домашнее задание).
(домашнее задание).
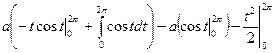 =
= 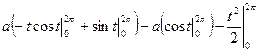 =
= 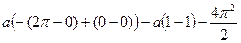 =
=  .
.
Практика № 3.
Задача 13.
Найти работу векторного поля 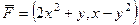 по перемещению точки по участку параболы
по перемещению точки по участку параболы 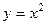 , где
, где 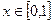 .
.
Решение. Здесь используем формулу для явно заданной кривой:
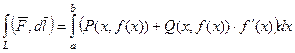 .
.
Все 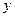 , которые встречаются в записи компонент векторного поля, надо выразить в виде
, которые встречаются в записи компонент векторного поля, надо выразить в виде 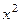 . Очевидно также, что
. Очевидно также, что 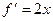 Итак:
Итак:
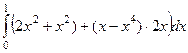 =
= 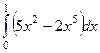 =
= 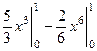 =
=
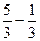 =
= 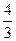 .
.
Ответ.  .
.
Задача 13-А (домашняя аналогичная № 13).
Найти работу векторного поля 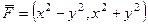 по перемещению точки по участку кубической параболы
по перемещению точки по участку кубической параболы 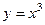 , где
, где 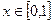 .
.
Ответ. 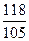 .
.
Задача 14.
Найти работу векторного поля 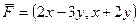 по перемещению точки по половине эллипса, заданного параметрически:
по перемещению точки по половине эллипса, заданного параметрически:
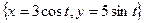 ,
, 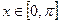 .
.
Решение. Здесь используем формулу для параметрически заданной кривой: 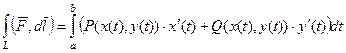 .
.
При этом учитываем, что 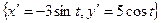 . При этом все
. При этом все 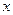 и
и 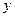 , которые встречаются в записи компонент векторного поля, надо выразить в виде
, которые встречаются в записи компонент векторного поля, надо выразить в виде 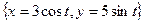 .
.
|
|
|
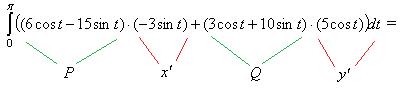
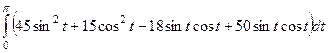 =
=
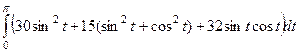 =
=
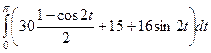 =
= 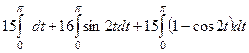 =
= 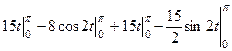 =
= 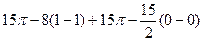 =
=
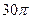 . Ответ.
. Ответ. 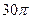 .
.
В следующих задачах кривые будут замкнутые, и в них будем применять формулу Грина, доказанную на лекции: 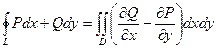 .
.
Наиболее удобно её применение именно в тех случаях, когда граница состоит из нескольких частей, ведь работу векторного поля надо было бы отдельно вычислять по каждой части (у которой своё уравнение в плоскости), а двойной интеграл сразу по единой плоской области.
Задача 15.
Найти циркуляцию векторного поля 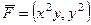 по перемещению точки по границе верхнего полукруга радиуса 1 двумя методами:
по перемещению точки по границе верхнего полукруга радиуса 1 двумя методами:
А). без формулы Грина. Б). по формуле Грина.
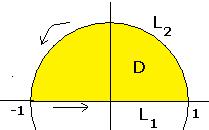
Решение.
Решение А). без формулы Грина. В этом случае нужно для каждого участка - отрезка 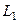 и полуокружности
и полуокружности  - вычислить работу поля отдельно. Чтобы обход всего контура осуществлялся один раз и против часовой стрелки, надо, чтобы движение по отрезку было слева направо
- вычислить работу поля отдельно. Чтобы обход всего контура осуществлялся один раз и против часовой стрелки, надо, чтобы движение по отрезку было слева направо 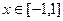 (при этом
(при этом 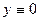 , и
, и 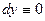 ), а по полуокружности справа налево, т.е. на ней использовать обычный метод параметрического задания точек:
), а по полуокружности справа налево, т.е. на ней использовать обычный метод параметрического задания точек: 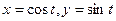 .
.
По 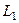 :
: 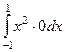 = 0.
= 0.
По  :
:  =
=
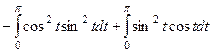 , во втором интеграле очевидно, подведение под знак дифференциала, а в первом есть несколько путей решения:
, во втором интеграле очевидно, подведение под знак дифференциала, а в первом есть несколько путей решения:
1) с помощью замены, учитывая то, что суммарная степень чётна (изучали во 2 семестре).
|
|
|
2) применить формулу понижения степени к каждому из квадратов.
3) использовать то, что 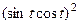 и формулу
и формулу 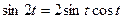 .
.
Наиболее оптимальным наверное, здесь будет 3-й путь.
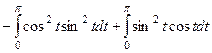 =
= 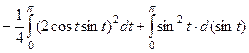
= 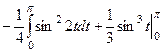 =
= 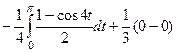 =
=
 =
= 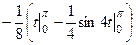 =
= 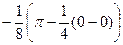 =
= 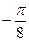 .
.
Решение Б). По формуле Грина.
Если 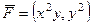 то
то 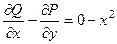 .
.
Двойной интеграл по полукругу вычисляется с помощью полярных координат, это стандартная задача, которые решали во 2 семестре. Так как полукруг в верхней полуплоскости, то 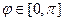 , а радиус 1,
, а радиус 1, 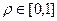 .
.
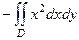 =
= 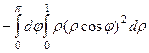 =
= 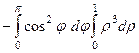 =
=
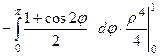 =
= 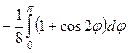 =
= 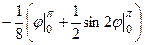 =
=  =
= 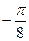 .
.
Ответ. 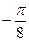 .
.
Задача 16.
Найти циркуляцию векторного поля 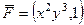 по перемещению точки по треугольнику с вершинами (0,0), (0,1), (1,1) с помощью формулы Грина.
по перемещению точки по треугольнику с вершинами (0,0), (0,1), (1,1) с помощью формулы Грина.
Решение. Если не использовать формулу Грина, то на каждой из сторон - горизонтальной, вектикальной и наклонной - надо было бы отдельно провести вычисление работы поля. Используя формулу Грина, мы вычислим лишь один двойной интеграл.
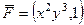
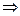
 .
.
Чертёж этого треугольника:
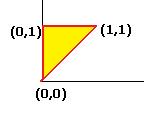
Далее следует стандартный метод вычисления двойного интеграла, изученный в прошлом семестре. Сначала спроецируем фигуру на ось Ох и найдём глобальные границы по  , это
, это 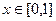 . При каждом конкретном
. При каждом конкретном  высота изменяется от наклонной линии
высота изменяется от наклонной линии 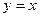 до горизонтальной
до горизонтальной  , то есть
, то есть 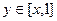 . Итак,
. Итак,
|
|
|
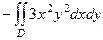 =
= 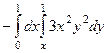 =
= 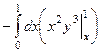 =
= 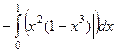 =
=  =
= 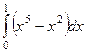 =
= 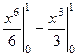 =
= 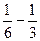 =
= 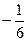 .
.
Ответ. 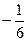 .
.
Задача 17.
Найти циркуляцию 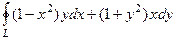 где L - это граница четверти круга радиуса 1 (лежащего в 1-й четверти).
где L - это граница четверти круга радиуса 1 (лежащего в 1-й четверти).
Решение. 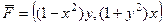
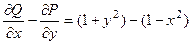 =
=
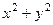 . Если бы мы не применяли формулу Грина, то пришлось бы 3 раза вычислять работу силы по трём разным участкам, из которых состоит этот замкнутый контур: часть окружности, горизонтальный и вертикальный отрезки. Чертёж:
. Если бы мы не применяли формулу Грина, то пришлось бы 3 раза вычислять работу силы по трём разным участкам, из которых состоит этот замкнутый контур: часть окружности, горизонтальный и вертикальный отрезки. Чертёж:
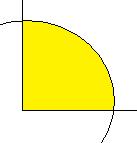
А по формуле Грина надо найти двойной интеграл по четверти круга, с очевидным переходом к полярным координатам.
 =
= 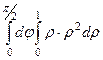 =
= 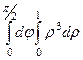 =
=  =
=
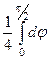 =
= 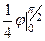 =
= 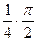 =
= 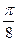 .
.
Ответ. 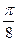 .
.
Контрольная работа
(30 минут, по 15 минут на задачу).
Задача 1. Тройной интеграл в сферических координатах.
Задача 2. Криволинейный интеграл 1-го рода.
Практика № 4.
Дата добавления: 2019-01-14; просмотров: 174; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
