Метод наибольшего правдоподобия
Требования к диагностическим тестам.. 3
Основные формы и виды тестов. 4
Составление тестов и определение их области содержания. 4
Модели и методы диагностики знаний. 5
Однопараметрическая модель Раша. 6
Оценивание параметров функции успеха в однопараметрической модели Раша. 11
Метод моментов. 12
Метод наибольшего правдоподобия. 17
Анализ точности оценивания параметров функции успеха. 20
Точность исходных измерений. 20
Проверка адекватности модели Раша с помощью χ2 - критерия Пирсона. 23
Проверка равномерности распределения дистракторов и эффективности их работы.. 26
Влияние числа дистракторов на точность оценивания уровня знаний. 27
Дифференцирующая (разрешающая) способность теста. 28
Оценка различающей способности тестовых заданий с помощью точечно-бисериального коэффициента. 29
Шкалы оценок в диагностическом тестировании. 30
Шкала первичных баллов. 31
Дробная и политомическая оценка результатов тестирования. 32
Нормативная шкала. 35
Метрическая шкала. 37
Перенос результатов тестирования различных выборок испытуемых на метрическую шкалу. 38
Использование перекрытия вариантов тестов. 38
Использование достаточных статистик. 41
Преобразование метрической шкалы в нормированную.. 42
Увеличение дифференциации результатов тестирования. 43
IRT - теория моделирования и параметризации педагогических тестов. 45
Оценивание параметров функции успеха в модели Бирнбаума. 48
Построение единой метрической шкалы в модели Бирнбаума при использовании параллельных вариантов теста 50
Метод линейной регрессии. 52
Метод промежуточной шкалы.. 53
Метод сопоставления функций успеха. 54
Анализ качества диагностических материалов. 57
Оценка надежности нормативно-ориентированного теста. 59
Оценка надежности критериально-ориентированного теста. 60
Стандартная ошибка тестовых измерений. 62
Оценка валидности диагностических тестов. 62
Адаптивное тестирование. 64
Психологическое тестирование. 65
Назначение психодиагностики и классификация ее методов. 65
Основные требования к психологическим тестам.. 67
Определение норм для теста. 68
Валидность. 69
Надежность. 70
Психологические тесты, имеющие связь с диагностикой знаний. 72
Тесты интеллекта. 72
Тесты способностей. 73
Тесты достижений. 74
Критериально-ориентированные тесты.. 74
Литература. 74
Требования к диагностическим тестам
Выделяют пять общих требований к тестам контроля знаний:
- валидность;
- определенность (общепонятность);
- простота;
- однозначность;
- надежность.
Валидность теста – это адекватность. Различают содержательную и критериальную (функциональную) валидность: первая – это соответствие теста содержанию контролируемого учебного материала, вторая – соответствие теста оцениваемому уровню деятельности.
Выполнение требования определенности (общедоступности) теста необходимо не только для понимания каждым учеником того, что он должен выполнить, но и для исключения правильных ответов, отличающихся от эталона.
Требование простоты теста означает, что тест должен иметь все задания примерно одного уровня сложности, т.е. он не должен быть комплексным и состоять из заданий разного уровня сложности.
Однозначность определяют как одинаковость оценки качества теста разными экспертами. Для выполнения этого требования тест должен иметь эталон.
Требование надежности заключается в обеспечении устойчивости результатов многократного тестирования одного и того же испытуемого.
При реализации систем компьютерного тестирования необходимо придерживаться именно этих пяти требований к создаваемым тестам. Однако реализация описанных выше условий к тестам еще не означает того, что созданный комплекс будет отвечать всем требованиям, предъявляемым к системам тестирования.
Основные формы и виды тестов
Следует различать два основных подхода к разработке тестов для конкурсного (профессионального отбора) и для аттестации учащихся [1,2]: нормативно-ориентированный и критериально – ориентированный. Первый подход позволяет сравнивать учебные достижения (уровень знаний и умений) отдельных испытуемых друг с другом на основе распределения баллов. А критериально - ориентированный подход позволяет оценивать, в какой степени испытуемый овладел необходимым для профессиональной деятельности учебным материалом. Оба эти подхода в равной степени необходимы для создания диагностических тестов в интеллектуальных обучающих системах.
Между нормативно-ориентированными и критериально-ориентированными тестами существует ряд различий [2], заключающихся не в самих тестовых заданиях, а в интерпретации индивидуальных баллов. Первое различие - цели создания теста. Нормативно-ориентированные тесты позволяют оценить соответствие знаний и умений испытуемого некоторой норме: подходит - не подходит. Критериально - ориентированные тесты дают возможность оценки уровня обученности и эффективности программы обучения. Второе различие – уровень детализации области содержания. От критериально – ориентированных тестов чаще всего требуется большая детализация. Третье различие – статистическая обработка. Обработанные (шкалированные) баллы по результатам нормативно – ориентированного тестирования базируются на статистических данных нормативной группы, то есть специфической достаточно большой выборке испытуемых, для чего применяются специальные нормативные шкалы. Кроме того, существует и ряд других отличий.
В настоящее время наибольшее распространение получили следующие формы тестовых заданий:
- закрытая, предполагающая выбор одного или более правильных вариантов ответов из числа предложенных;
- форма на установление соответствия между двумя предложенными множествами;
- открытая форма с ограничениями на ответ, предполагающая ввод в качестве ответа одного или нескольких чисел, слов или формул;
- форма на установление правильной последовательности.
Введение в тест заданий с многовариантными ответами развивает потребность в поиске разных путей решения задачи, что необходимо для достижения основной цели обучения умения самостоятельно выбирать способ выполнения поставленной задачи.
Использование компьютеров расширяет возможности в применении различных форм тестов. В частности возможна автоматическая проверка текстовых ответов.
Составление тестов и определение их области содержания
При изучении любой учебной дисциплины есть особенно важные темы, без знания которых невозможно усвоение более сложного материала в процессе учебы или которые будут необходимы в работе по специальности. Важность каких-либо разделов курса можно учесть, увеличив долю вопросов по этим разделам в общем количестве вопросов. Однако наиболее важные разделы не всегда содержат больше всего материала.
При составлении заданий теста следует соблюдать ряд правил, необходимых для создания надежного, сбалансированного инструмента оценки знаний. В первую очередь, необходимо проанализировать содержание заданий с позиции равной представлености в тесте разных учебных тем, понятий, и т.д. Тест не должен быть нагружен второстепенными терминами, несущественными деталями с акцентом на механическую память. Задания теста должны быть сформулированы четко, кратко и недвусмысленно, чтобы все учащиеся понимали смысл того, что у них спрашивается. Важно проследить, чтобы ни одно задание теста не могло служить подсказкой для ответа на другое [3].
Варианты ответов на каждое задание должны подбираться таким образом, чтобы исключались возможности простой догадки или отбрасывания заведомо неподходящего ответа.
Важно выбирать наиболее приемлемую форму ответов на задания. Учитывая, что задаваемый вопрос должен быть сформулирован коротко, желательно также кратко и однозначно формулировать ответы. Например, удобна альтернативная форма ответов, когда учащийся должен подчеркнуть одно из перечисленных решений “да-нет”, “верно-неверно”.
Задачи для тестов должны быть информативными, отрабатывать одно или несколько понятий, определений и т.д. При этом тестовые задачи не должны быть слишком громоздкими или слишком простыми. Вариантов ответов на задачу должно быть, по возможности, не менее пяти, а в качестве неверных ответов желательно использовать наиболее типичные ошибки [4].
Для аттестации студентов можно использовать критериально-ориентированные тесты. При этом необходимо решить задачу измерения уровня обученности для большой области знаний, навыков и умений, с учетом степени важности и объема изучаемого материала в разделах курса. Для этого необходимо:
1) определить область содержания и цель тестирования, провести анализ учебной дисциплины и отобрать материал для теста;
2) задать ограничения и выбрать подходы к процессу разработки, создать план теста и его спецификацию;
3) создать задания и провести их анализ экспертами для оценки конгруэнтности области содержания и целям тестирования;
4) провести пробное тестирование и проанализировать его результаты;
5) выбрать стандарты оценивания;
6) оценить надежность и валидность (критериальной и конструктной) теста;
7)окончательная доработка теста и его параллельных форм.
Модели и методы диагностики знаний
При создании тестов возникают определенные трудности в части формирования шкалы оценок выполнения заданий. Традиционная Российская система оценивания знаний обучаемых основана на лингвистических оценках, по которым проставляются записи в зачетных книжках за период обучения, производится учет успеваемости, устанавливается стипендия и т.д.
Очевидно, что при формировании такой шкалы оценок велика доля субъективизма, поскольку здесь многое зависит от опыта, интуиции, компетентности и профессионализма преподавателя. Кроме того, требования, предъявляемые разными преподавателями к уровню знаний студентов, колеблются в очень широких пределах.
При формировании шкалы оценок довольно часто встречается метод “проб и ошибок”. Поэтому реальные знания учащегося не получают объективного отражения и как негативное последствия - снижается стимулирующее воздействие экзаменационной оценки на познавательную деятельность и качество учебного процесса в целом.
В некоторых моделях тестирования оценивание результатов производится только по факту правильности ответа, т.е. ход решения в задачах не проверяется и не оценивается. Таковы, например, закрытые задания с однозначным числовым ответом или бинарные тесты.
Первичной информацией при тестировании знаний является набранный балл испытуемых или так называемый первичный балл. Достоинством этой оценки является ее простота и наглядность, Действительно, чем больше заданий выполнил испытуемый, тем выше его балл.
Однако проблема заключается в том, что первичный балл является не абсолютной, а относительной оценкой. Он существенно зависит от трудности заданий теста и на другом тесте он может оказаться иным, причем сама трудность теста в свою очередь определяется всем контингентом испытуемых. Желательно иметь объективную оценку уровня подготовленности испытуемых, подтверждаемую на различных тестах, имеющих заранее определенный уровень трудности заданий.
Вторым существенным недостатком первичных баллов является их нелинейность по отношению к тем параметрам, которые они должны характеризовать (уровень подготовленности). В частности, если тест состоит из 100 заданий, то разность в первичных баллах b1-b2=86-82=4 соответствует большему различию в уровне подготовленности участников, чем та же разность для участников имеющих, например 23 и 19 баллов. Сравнивая первичные баллы необходимо понимать, что первичные баллы являются лишь индикатором подготовленности испытуемых, а не ее мерой.
Любая информация для ее последующего применения в заданиях теста должна быть представлена определенным количественным показателем, рассчитанным с использованием условной единицы образовательной информации.
Однопараметрическая модель Раша
Статистическая обработка результатов тестирования на основе модели Раша обладает важными достоинствами, среди которых, необходимо отметить следующие.
Модель Раша превращает измерения, сделанные в дихотомических и порядковых шкалах в линейные измерения, в результате качественные данные анализируются с помощью количественных методов. Это позволяет использовать широкий спектр статистических процедур.
Оценка трудности тестовых заданий не зависит от выборки испытуемых, на которых была получена и оценка уровня знаний испытуемых аналогично не зависит от используемого набора тестовых заданий. Пропуск данных для некоторых комбинаций (испытуемый ÷ тестовое задание) не является критическим. Кроме того, модель Раша характеризуется наименьшим числом параметров: один параметр уровня знаний для каждого испытуемого и только один параметр трудности для каждого задания.
Модель Раша опирается на понятия "трудность задания" и "уровень подготовленности". Так, одно задание считается более трудным, чем другое, если вероятность правильного ответа на первое задание меньше, чем на второе, независимо от того, кто их выполняет. Аналогично, более подготовленный студент имеет большую вероятность правильно ответить на все задания, чем менее подготовленный.
Благодаря простой структуре модели существуют удобные вычислительные процедуры для проверки адекватности модели: для всего набора тестовых результатов, для каждого испытуемого, для каждого задания и для каждого конкретного ответа.
Рассмотрим модель Раша более подробно. Пусть тест состоит из К различных заданий бинарного типа), пытуемый получает 1, если ответил правильно и 0 при неверном ответе) и его выполняют N – студентов. В результате получается матрица ответов An,k состоящая из N- строк (i) и К –столбцов (j).
An,k=(aij)
Число bi равное сумме баллов в i- строке называется первичным баллом i- испытуемого (оно равно числу его правильных ответов):
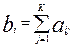
При необходимости первичный балл можно выразить в процентах (или долях) следующим образом  100%. Уровни подготовленности участников A и B обозначим через Sa и Sb, а трудность заданий через t (на самом деле все задания имеют разный уровень трудности tk). В модели Раша доказывается, что:
100%. Уровни подготовленности участников A и B обозначим через Sa и Sb, а трудность заданий через t (на самом деле все задания имеют разный уровень трудности tk). В модели Раша доказывается, что:
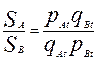 (1)
(1)
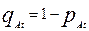
 ,
,
где 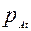 и
и 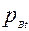 - вероятность выполнения задания уровня трудности t соответственно участниками A и B,
- вероятность выполнения задания уровня трудности t соответственно участниками A и B, 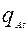 и
и 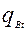 - вероятности невыполнения задания уровня трудности t соответственно участниками A и B. Из общих соображений выражение (1) должно быть верным для любого уровня трудности заданий и любой пары участников тестирования. Пусть, какое либо задание имеет трудность t=1 и необходимо сравнить трудности двух заданий. В модели Раша уровень трудности определяется, как отношение вероятности (
- вероятности невыполнения задания уровня трудности t соответственно участниками A и B. Из общих соображений выражение (1) должно быть верным для любого уровня трудности заданий и любой пары участников тестирования. Пусть, какое либо задание имеет трудность t=1 и необходимо сравнить трудности двух заданий. В модели Раша уровень трудности определяется, как отношение вероятности (  ) того, что некоторый стандартный участник испытания с единичным уровнем подготовки (S=1) не выполнит данное задание к вероятности (
) того, что некоторый стандартный участник испытания с единичным уровнем подготовки (S=1) не выполнит данное задание к вероятности ( 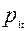 ) его выполнения:
) его выполнения:
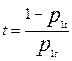 .
.
Единичный уровень подготовки и единичная трудность задания в модели Раша связаны между собой. Используя выражение:
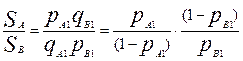 ,
,
и предположив, что уровень подготовленности именно участника В является единичным ( 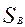 =1) получим следующее выражение:
=1) получим следующее выражение:
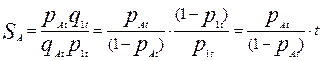 (2)
(2)
Уравнение (2) связывает уровень трудности некоторого задания и уровень подготовленности некоторого участника с вероятностью правильного выполнения задания и должно быть справедливо для заданий любого уровня трудности. Учитывая общность полученного уравнения (2) можно показать, что вероятность Р(S,t), того, что участник с уровнем подготовки S правильно выполнит задание трудности t, выражается следующей формулой:
 (3)
(3)
Вероятность Р(S,t) получила название функции успеха. Как видно из выражения (3) функция успеха зависит только от отношения t к S, поэтому модель Раша называется однопараметрической и использует шкалу отношений.
Вводя новые переменные:
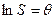 ,
,  ,
,
 ,
, 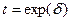
Выражение (3) можно переписать в виде:
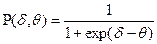 (4)
(4)
Формула (4) является основным уравнением однопараметрической логистической модели Раша, единица измерения δ и θ называется логитом. При одном логите (δ0=1 и θ0=1) вероятность успеха 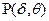 =0,5, т.е. вероятность выполнения стандартного задания стандартным участником должна быть равна 0,5 (см. рис.1). Модель Раша позволяет сделать
=0,5, т.е. вероятность выполнения стандартного задания стандартным участником должна быть равна 0,5 (см. рис.1). Модель Раша позволяет сделать

Рис.1. Характеристическая кривая трудности задания
один очень важный вывод: чем выше уровень подготовки участника, тем больше вероятность выполнения задания любого уровня трудности. Стоит отметить, что параметры δ и θ называют латентными параметрами, т.к. они не измеряются непосредственно в процессе тестирования.
Функция успеха может быть получена исходя их принципа максимума информации ( 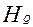 ) о системе (минимума энтропии (
) о системе (минимума энтропии ( 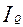 )) [5]. Для этого введем следующие характеристики:
)) [5]. Для этого введем следующие характеристики:
 -среднее значение тестового балла участника тестирования по всей выборке заданий (К - число заданий в тесте), иными словами средняя успешность выполнения всех К заданий i- испытуемым;
-среднее значение тестового балла участника тестирования по всей выборке заданий (К - число заданий в тесте), иными словами средняя успешность выполнения всех К заданий i- испытуемым;
 - среднее значение балла задания теста по всей выборке испытуемых (N- число участников тестирования), иными словами средняя успешность выполнения j –задания всеми N испытуемыми.
- среднее значение балла задания теста по всей выборке испытуемых (N- число участников тестирования), иными словами средняя успешность выполнения j –задания всеми N испытуемыми.
Число bi равное сумме баллов в i- строке называется первичным баллом i- испытуемого (оно равно числу его правильных ответов):
 ,
,
а число cj равное сумме баллов в k- столбце называется первичным баллом j- задания (оно равно числу правильных ответов на это задание всеми испытуемыми):
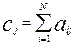 .
.
Количество различных состояний системы (число способов распределения 0 и 1 в матрице ответов An,k=(aij)), при заданном значении первичного балла j-задания  определяется числом сочетаний (
определяется числом сочетаний ( 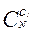 ) по
) по  из N:
из N:
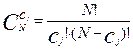 ,
,
а полное число состояний системы W с учетом изменения j от 1 до К будет равно:
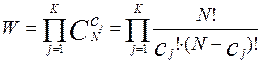 .
.
Информационная энтропия 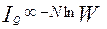 ,
,
где 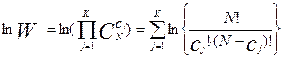 .
.
Используя формулу Стирлинга можно получить следующую формулу:
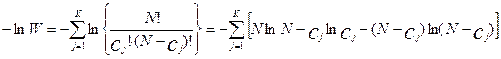 .
.
Чтобы найти распределение, соответствующее наибольшему статистическому весу W рассмотрим вариацию  , соответствующую максимуму информации (
, соответствующую максимуму информации (  ) о системе (минимума энтропии (
) о системе (минимума энтропии ( 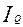 )):
)):
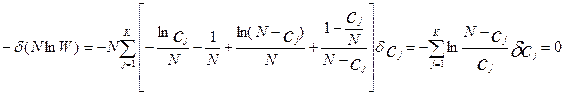
или: 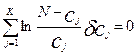
Вариации  выбираются произвольно, за исключением некоторого их числа равного числу дополнительных условий (множителей Лагранжа). Все вариации
выбираются произвольно, за исключением некоторого их числа равного числу дополнительных условий (множителей Лагранжа). Все вариации  можно рассматривать как независимые друг от друга, а зависящими от них величинами считать множители Лагранжа. Будем полагать одну из вариаций
можно рассматривать как независимые друг от друга, а зависящими от них величинами считать множители Лагранжа. Будем полагать одну из вариаций  ≠ 0, а остальные равными. Поэтому к выражению
≠ 0, а остальные равными. Поэтому к выражению  надо прибавить проварьированые дополнительные условия. В данном случае имеется всего лишь одно дополнительное условие, которое связывает набранный индивидуальный первичный балл i –испытуемого (
надо прибавить проварьированые дополнительные условия. В данном случае имеется всего лишь одно дополнительное условие, которое связывает набранный индивидуальный первичный балл i –испытуемого ( 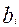 ) с первичным баллом j –задания:
) с первичным баллом j –задания:
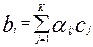 , где
, где 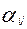 - множитель, определяющий успешность выполнения i –испытуемым j –задания.
- множитель, определяющий успешность выполнения i –испытуемым j –задания.
Индивидуальный балл i –испытуемого является определенным в результате тестирования, поэтому его вариация  равна 0.
равна 0.
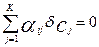
Таким образом:
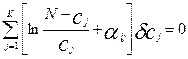 .
.
С учетом того, что 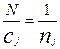 находим:
находим:
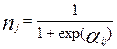 .
.
Сравнивая полученное выражение с формулой: 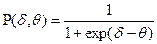
можно интерпретировать 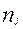 , как вероятность успеха, т.е. вероятность выполнения i –участником j – задания, а
, как вероятность успеха, т.е. вероятность выполнения i –участником j – задания, а 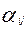 как (
как ( 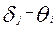 ) разность между трудностью j –задания и уровнем подготовленности i –участника, выраженную в логитах.
) разность между трудностью j –задания и уровнем подготовленности i –участника, выраженную в логитах.
Оценивание параметров функции успеха в однопараметрической модели Раша
При любом проведении процесса тестирования результаты вычисления  - статистических оценок
- статистических оценок  , где i=1, 2, ……..n, и
, где i=1, 2, ……..n, и 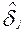 - статистических оценок
- статистических оценок  , где j=1, 2, ……..k будут отличаться от существующих точных значений
, где j=1, 2, ……..k будут отличаться от существующих точных значений  , где i=1, 2, ……..n, и
, где i=1, 2, ……..n, и  , где j=1, 2, ……..k. По своему физическому смыслу оценки являются определенными функциями исходных случайных значений элементов матрицы ответов An,k состоящей из N- строк (i) и К –столбцов (j)
, где j=1, 2, ……..k. По своему физическому смыслу оценки являются определенными функциями исходных случайных значений элементов матрицы ответов An,k состоящей из N- строк (i) и К –столбцов (j)
An,k=(aij)
и поэтому сами являются случайными величинами [6]. Таким образом, возникает вопрос о нахождении математических ожиданий и дисперсий этих случайных величин. Необходимо чтобы математическое ожидание соответствующих оценок совпадало с соответствующими точными значениями, а дисперсия оценки была бы минимальной [7,8].
Статистическая оценка уровня подготовленности  и уровня трудности
и уровня трудности 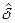 будут являться несмещенными оценками, если их математическое ожидание при любом объеме выборки испытуемых будет равно самому оцениваемому параметру, например:
будут являться несмещенными оценками, если их математическое ожидание при любом объеме выборки испытуемых будет равно самому оцениваемому параметру, например: 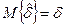 .
.
Смещенные оценки приводят к сдвигу оцениваемых параметров относительно истинных значений, и их следует избегать. Однако на практике бывает трудно установить факт смещения или не удается получить не смещенную оценку, но и смещенная оценка позволяет получить неплохое оценивание, если дисперсия оцениваемого параметра достаточно велика. В реальности дисперсия не может быть меньше определенного предела, обусловленного количеством исходных данных. На практике обычно используют асимптотически не смещенную оценку, математическое ожидание которой стремится к истинному значению оцениваемого параметра, при неограниченном увеличении объема выборки.
Статистическая оценка называется эффективной если при заданной выборке, она имеет возможную наименьшую дисперсию D* при неполной информации, возможно, получить лишь оценку с D>D*. Если отношение D/D*→1, при увеличении выборки, то оценка называется асимптотически эффективной.
Статистическая оценка называется состоятельной, если несмещенная оценка не является эффективной, но при увеличении объема выборки ее дисперсия уменьшается.
Несмещенность, эффективность и состоятельность являются независимыми свойствами, характеризующими оценки с разных сторон. Задача отыскания эффективных несмещенных оценок имеет особо важное значение при обработке результатов малых выборок испытуемых.
Метод моментов
Для оценки параметров функции успеха (δ и θ) необходимо провести тестирование какого либо числа испытуемых N с помощью некоторого числа бинарных заданий К и построить матрицу ответов An,k состоящую из N- строк (i) и К –столбцов (j).
An,k=(aij)
Число bi равное сумме баллов в i- строке называется (как и раньше) первичным баллом i- испытуемого (оно равно числу его правильных ответов):
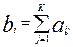 ,
,
а число cj равное сумме баллов в k- столбце называется (как и раньше) первичным баллом j- задания (оно равно числу правильных ответов на это задание):

Необходимо найти:
 - статистическую оценку
- статистическую оценку  , где i=1, 2, ……..n,
, где i=1, 2, ……..n,
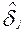 - статистическую оценку
- статистическую оценку  , где j=1, 2, ……..k.
, где j=1, 2, ……..k.
И оценить точность  и
и 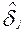 , т.е. найти
, т.е. найти 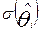 и
и 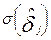 . Не вдаваясь в подробности [6-8], кратко рассмотрим, как найти
. Не вдаваясь в подробности [6-8], кратко рассмотрим, как найти  ,
, 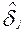 ,
, 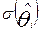 и
и 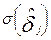 . Пусть участник с номером - i выполняет К заданий. Вероятность выполнения составляет Pi1-для первого задания, Pi2-для второго, Pi3 –для третьего, и т.д. до Pik. Случайные элементы (aij) матрицы ответов являются индикаторами успешного решения i – участником j- задания (aij принимают значения 1 или 0). Поэтому, математическое ожидание aij (М{aij}) просто равно вероятности Pij , а дисперсия aij (D{aij}) равна произведению Pij и qij (вероятность неправильного ответа i –участника на j- задание). Математическое ожидание M{bi} первичного балла i- испытуемого будет равно:
. Пусть участник с номером - i выполняет К заданий. Вероятность выполнения составляет Pi1-для первого задания, Pi2-для второго, Pi3 –для третьего, и т.д. до Pik. Случайные элементы (aij) матрицы ответов являются индикаторами успешного решения i – участником j- задания (aij принимают значения 1 или 0). Поэтому, математическое ожидание aij (М{aij}) просто равно вероятности Pij , а дисперсия aij (D{aij}) равна произведению Pij и qij (вероятность неправильного ответа i –участника на j- задание). Математическое ожидание M{bi} первичного балла i- испытуемого будет равно:
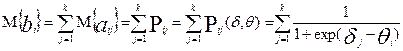 ,
,
математическое ожидание M{cj} первичного балла j- задания будет равно:
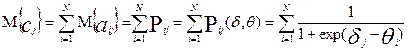 .
.
Далее приравниваем математическое ожидание первичных баллов самим первичным баллам. Пирсон [7,8] доказал, что в этом случае получаются достаточно хорошие несмещенные оценки (их дисперсия при увеличении выборки стремится к 0). Таким образом, получаем следующую систему уравнений:
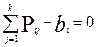
N-уравнений по числу участников, содержащих (N+K) неизвестных,
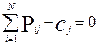
K-уравнений по числу заданий, содержащих (N+K) неизвестных.
В модели Раша [6,9,10] первичные баллы являются достаточными статистиками и
(N+K)<NK, т.е. задачу можно редуцировать (уменьшить число уравнений, которые необходимо решать). Число различных значений θ будет равно числу различных значений первичного балла, а не N (участники, получившие все 0 и все 1 должны быть исключены). Поскольку, число возможных значений первичного балла равно (K-1), то число уравнений будет равно (2K-1). Система из (2K-1) нелинейных уравнений может быть решена методом итераций путем линеаризации уравнений [6]. Напомним, что
 .
.
Пусть необходимо решить нелинейное уравнение вида:
f(x)=0,
где f(x) – заданная дважды дифференцируемая функция, и для искомого корня известно приближенное значение Х0 . Разложим функцию f(x) в окрестности точки Х0 в ряд Тейлора и ограничимся двумя первыми членами:
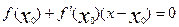 .
.
Далее находим, что:
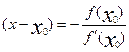 ,
,
а для итерационной процедуры:
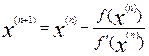 , где n – номер последовательного итерационного приближения.
, где n – номер последовательного итерационного приближения.
Производные левых частей уравнений:
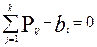
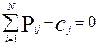
имеют следующий вид:
 , где
, где 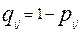
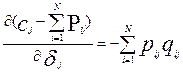 ,
,
а для нахождения соответствующих итерационных приближений можно записать:
 , где b=0, 1, 2, ……….K
, где b=0, 1, 2, ……….K
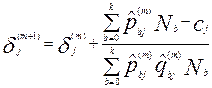 , где j=1, 2, 3, ……K.
, где j=1, 2, 3, ……K.
Здесь b- номер группы участников, набравших один и тот же первичный балл, Nb- количество участников в группе b, 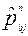 ,
,  ,
, 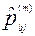 ,
, 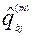 - статистические оценки вероятностей, вычисляемые с использованием формулы:
- статистические оценки вероятностей, вычисляемые с использованием формулы:
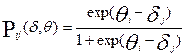
по имеющимся приближенным значениям латентных параметров. В результате получим:
 ,
, 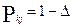 ,
,
где Δ- малое положительное число (например: 0,005).
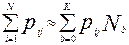
Для вычисления соответствующих приближений используют следующую схему [10,11]:
Полагают n=0 и вычисляют начальные приближения  для каждого b:
для каждого b:
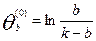 , b=1, 2, 3, ……k-1
, b=1, 2, 3, ……k-1
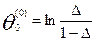 ,
, 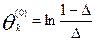
затем находят среднее значение

и центруют оценки 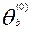 , т.е. вычисляем уклонения:
, т.е. вычисляем уклонения:
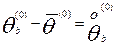
Полагают m=0 и вычисляют начальные приближения  для каждого j:
для каждого j:
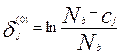 , j=1, 2, 3, ………K.
, j=1, 2, 3, ………K.
Очередное приближение 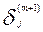 вычисляют по формуле:
вычисляют по формуле:
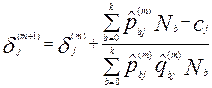 ,
,
где 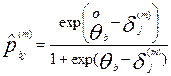
до тех пор пока не будет выполнено неравенство:
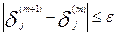 , для любого j=1, 2, 3, …….K,
, для любого j=1, 2, 3, …….K, 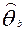 - имеющиеся к данному моменту центрированные оценки уровня подготовленности испытуемых, ε- малая положительная величина (ε<<∆).
- имеющиеся к данному моменту центрированные оценки уровня подготовленности испытуемых, ε- малая положительная величина (ε<<∆).
Вычисляют очередное приближение 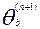 по формуле:
по формуле:
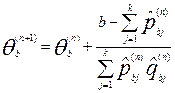 ,
,
где 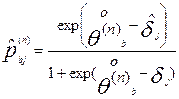
до тех пор пока не будет выполнено неравенство:
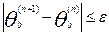 , для любого b=1, 2, 3, …….K-1,
, для любого b=1, 2, 3, …….K-1,
 - имеющиеся к данному моменту оценки уровня трудности заданий. Затем находят среднее значение
- имеющиеся к данному моменту оценки уровня трудности заданий. Затем находят среднее значение
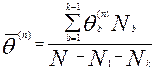
и центруют оценки 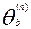 , т.е. вычисляют уклонения:
, т.е. вычисляют уклонения:
 .
.
Затем вычисляют среднеквадратичное отклонение оценок очередного приближения от аналогичных оценок предыдущей итерации:
 ,
,
Если σ>ε/3, то переходят к пункту 3, если σ≤ε/3 то вычисления заканчивают.
Оценки уровня подготовленности участников тестирования 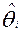 и уровней трудности заданий
и уровней трудности заданий  характеризуют взаимное расположение латентных параметров на единой шкале логитов, но не их независимые значения (шкала не нормированная, а метрическая), нет информации определяющей начало отсчета. Замена
характеризуют взаимное расположение латентных параметров на единой шкале логитов, но не их независимые значения (шкала не нормированная, а метрическая), нет информации определяющей начало отсчета. Замена 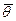 =0 на
=0 на 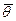 =1 лишь смещает оценки по шкале на 1, не меняя их взаимного расположения.
=1 лишь смещает оценки по шкале на 1, не меняя их взаимного расположения.
Для выявления возможного сдвига оценок параметров тестирования необходимо, чтобы различные варианты теста имели общие задания или часть испытуемых выполнила все варианты. Предельным является случай, когда каждый испытуемый получает случайный набор заданий из общей базы, причем на всей выборке испытуемых будут использованы все задания базы, а число заданий в базе превосходит общее число задаваемых данному испытуемому вопросов. Эта проблема будет детально обсуждена в параграфе: Модель педагогического тестирования, при случайном выборе K заданий из множества M (модель “K из M”).
Метод наибольшего правдоподобия
Данный метод основывается на использовании функции правдоподобия [6,8]. В применении к тестированию функция правдоподобия L дискретной случайной величины балла aij будет функцией аргументов  и
и 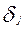 , представляющей произведение вероятностей
, представляющей произведение вероятностей 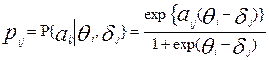 для всевозможных значений i и j:
для всевозможных значений i и j:
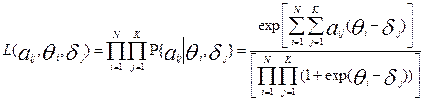
В качестве точечных оценок латентных параметров принимают такие значения 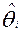 и
и 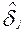 , при которых функция правдоподобия
, при которых функция правдоподобия  достигает максимума),кие оценки называют оценками наибольшего правдоподобия). Необходимо отметить, что функции
достигает максимума),кие оценки называют оценками наибольшего правдоподобия). Необходимо отметить, что функции 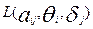 и
и  достигают максимума при одних и тех же значениях своих аргументов, поэтому более удобно искать максимум функции
достигают максимума при одних и тех же значениях своих аргументов, поэтому более удобно искать максимум функции 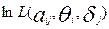 . В данном случае:
. В данном случае:
 ,
,
где  и
и  - соответственно первичные баллы участников и заданий.
- соответственно первичные баллы участников и заданий.
Логарифмическая функция правдоподобия зависит только от первичных баллов 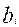 и
и 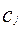 , являющихся достаточными статистиками исходных наблюдений. Для нахождения максимума функции правдоподобия приравняем нулю частные производные логарифмической функции правдоподобия по каждому из аргументов:
, являющихся достаточными статистиками исходных наблюдений. Для нахождения максимума функции правдоподобия приравняем нулю частные производные логарифмической функции правдоподобия по каждому из аргументов:
 , i=1, 2, 3, ……N
, i=1, 2, 3, ……N
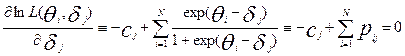 , j=1, 2, 3, ……K
, j=1, 2, 3, ……K
Данная система нелинейных уравнений называется системой уравнений правдоподобия и содержит (N+K) уравнений с (N+K) неизвестными латентными параметрами 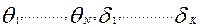 . Эта система имеет единственное решение, соответствующее максимуму логарифмической функции правдоподобия. В случае модели Раша наблюдается совпадение систем уравнений, получаемых в методе моментов и методе максимального правдоподобия. Следовательно, решение этих уравнений можно выполнить, используя все выше изложенные рассуждения. Для другой функции успеха уравнения правдоподобия будут иметь иной вид.
. Эта система имеет единственное решение, соответствующее максимуму логарифмической функции правдоподобия. В случае модели Раша наблюдается совпадение систем уравнений, получаемых в методе моментов и методе максимального правдоподобия. Следовательно, решение этих уравнений можно выполнить, используя все выше изложенные рассуждения. Для другой функции успеха уравнения правдоподобия будут иметь иной вид.
Метод наибольшего правдоподобия обладает следующими свойствами:
Получаемые оценки являются состоятельными, несмещенными и эффективными.
Оценки подчиняются нормальному распределению с параметрами:
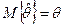 ,
,
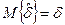 ,
,
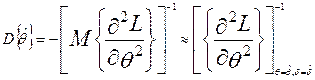 ,
, 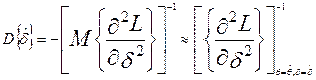
и имеют наименьшую дисперсию по сравнению с другими нормальными оценками. Дифференцирование по представленным формулам позволяет оценить в рамках модели Раша нижние границы дисперсий оценок латентных параметров:
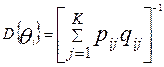 ,
, 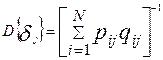
3) Если эффективные оценки существуют, то метод наибольшего правдоподобия дает именно эти оценки.
4) Метод наибольшего правдоподобия наиболее полно использует данные выборки об оцениваемом параметре и позволяет найти достаточные оценки, если они существуют. Однако, несмотря на 40-летний опыт применения этой модели во многих областях, прежде всего в образовании и психологии, до сих пор продолжаются дискуссии об истинной ценности и эффективности модели Раша. До сих пор существуют две крайние точки зрения на эту модель.
Наиболее убежденные сторонники модели Раша утверждают: "Можно ли собрать или построить или сформулировать данные так, чтобы они соответствовали определению измерения (модели Раша)? Если нет, — то такие данные бесполезны".
Их наиболее последовательные оппоненты утверждают следующее: "Данные — это данные, а модель — это конструкция исследователя, которая подвержена ошибкам". Например, при построении регрессии, выбрасывая те или иные данные, можно получить любую зависимость, но мы тем самым ограничиваем реальный мир данных. Таким образом, создается искусственная переменная, о которой мало что известно.
Для практики одним из наиболее важных критериев является точность оценивания. Чем больше точность, тем лучше работает модель. В случае отсутствия ошибок измерения любая модель в смысле точности измерения работает идеально. Но на практике ошибки всегда есть и поэтому важно знать, насколько точные оценки позволяет получать та или иная модель.
На основе имитационного моделирования можно исследовать точность оценивания уровня знаний и трудностей заданий. А также число итераций, требуемых для вычисления этих оценок (методом наибольшего правдоподобия) в многофакторной ситуации в зависимости от:
- диапазона уровней знаний испытуемых;
- диапазона трудностей заданий;
- степени соответствия диапазонов уровней знаний испытуемых и трудностей заданий;
- числа испытуемых;
- числа заданий;
- степени соответствия данных модели;
- доли пропущенных данных.
Для статистической обработки результатов моделирования используется многофакторный дисперсионный анализ.
Анализ точности оценивания параметров функции успеха
Точность исходных измерений
При диагностике знаний исходными величинами в модели Раша являются вероятности (  ) верного решения j- задания участниками, набравшими один и тот же первичный балл b. Эти вероятности определяются соответствующими несмещенными оценками – относительными частотами -
) верного решения j- задания участниками, набравшими один и тот же первичный балл b. Эти вероятности определяются соответствующими несмещенными оценками – относительными частотами - 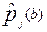 , имеющими дисперсию
, имеющими дисперсию 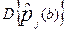 :
:
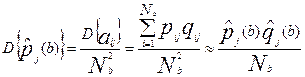
Однако последняя оценка является смещенной, поскольку
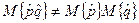
Символ M обозначает математическое ожидание.
 ,
,
где  .
.
Поэтому: 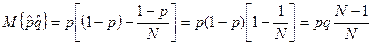 и
и
несмещенная оценка дисперсии относительной частоты  определяется формулой:
определяется формулой:
 ,
,
где 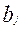 - количество участников, набравших балл b и правильно выполнивших задание с номером j. Таким образом:
- количество участников, набравших балл b и правильно выполнивших задание с номером j. Таким образом:
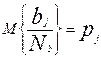 ,
,  ,
, 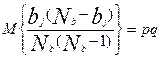
Оценим дисперсию оценки функции успеха ( 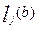 ) решить задание с номером- j, участником, набравшим b – баллов [6]:
) решить задание с номером- j, участником, набравшим b – баллов [6]:
 .
.
После дифференцирования данного уравнения получим:
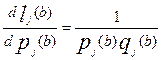
Дифференциалы можно заменить средними квадратичными ошибками (корень квадратный из дисперсии):
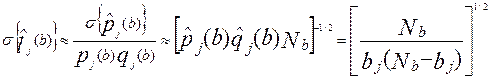
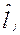 - средневзвешенное значение, причем:
- средневзвешенное значение, причем: 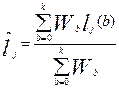 .
.
Величина 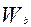 является статистическим весом (весовым коэффициентом) набранного балла b, т.е. она показывает, как часто данный набранный балл, встречается у участников тестирования среди различных комбинаций набранных баллов (0≤
является статистическим весом (весовым коэффициентом) набранного балла b, т.е. она показывает, как часто данный набранный балл, встречается у участников тестирования среди различных комбинаций набранных баллов (0≤ 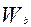 ≤1). Последнее равенство в формуле среднеквадратичной оценки предполагает, что
≤1). Последнее равенство в формуле среднеквадратичной оценки предполагает, что 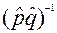 является хорошей оценкой для
является хорошей оценкой для  . Однако
. Однако
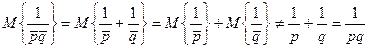
и поэтому оценка 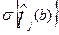 является смещенной. В случае биноминального распределения несмещенное оценивание 1/p невозможно [6, 9]. Однако [12]
является смещенной. В случае биноминального распределения несмещенное оценивание 1/p невозможно [6, 9]. Однако [12]
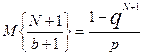
Следовательно, (N+1)/(b+1) является асимптотически несмещенной оценкой для 1/p. Поэтому, выражение:

является (по N) асимптотически несмещенной оценкой для  и
и

где 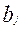 - количество участников, решивших j – задание и набравших по b – баллов,
- количество участников, решивших j – задание и набравших по b – баллов, 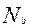 - общее количество участников набравших балл – b.
- общее количество участников набравших балл – b.
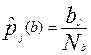 ,
, 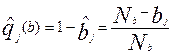
Легко заметить, что заметное отличие

от 
наблюдаются только при малых значениях  . Предположив некоррелированность случайных величин, для статистических оценок соответствующих дисперсий можно получить следующие формулы:
. Предположив некоррелированность случайных величин, для статистических оценок соответствующих дисперсий можно получить следующие формулы:
 ,
,
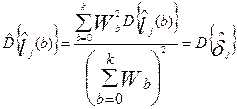 ,
,
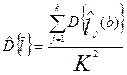 ,
,
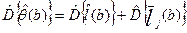
Последняя формула получена без учета ковариации между 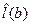 и
и  . Величина
. Величина 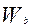 является статистическим весом (весовым коэффициентом) набранного балла b, т.е. она показывает, как часто данный набранный балл встречается у участников тестирования среди различных комбинаций набранных баллов (0≤
является статистическим весом (весовым коэффициентом) набранного балла b, т.е. она показывает, как часто данный набранный балл встречается у участников тестирования среди различных комбинаций набранных баллов (0≤ 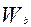 ≤1).
≤1).
Проверка адекватности модели Раша с помощью χ2 - критерия Пирсона
Если предположить справедливость модели Раша то разности 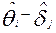 [6] позволяют вычислить теоретические вероятности
[6] позволяют вычислить теоретические вероятности 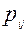 того, что i-участник испытания правильно выполнит j-задание:
того, что i-участник испытания правильно выполнит j-задание:
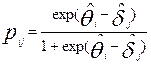 .
.
Первичные баллы делят всех N испытуемых на K+1 группу в зависимости от числа правильно выполненных заданий в тесте, причем уровень подготовленности  одинаков для всех участников, набравших одинаковый первичный балл- b. Введем следующие обозначения: Nb – количество испытуемых набравших по b – баллов, Nbj – количество испытуемых набравших b- баллов и правильно выполнивших j-задание (j=1, 2, 3, …. K).
одинаков для всех участников, набравших одинаковый первичный балл- b. Введем следующие обозначения: Nb – количество испытуемых набравших по b – баллов, Nbj – количество испытуемых набравших b- баллов и правильно выполнивших j-задание (j=1, 2, 3, …. K).
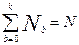
Для каждого значения b и j экспериментальное и теоретическое значение вероятностей будут соответственно равны:
 и
и  .
.
Возникает вопрос, насколько значимы различия между экспериментальными и теоретическими значениями вероятностей? Какие расхождения связанны со случайными отклонениями и ограниченностью данных, позволяющими считать, что модель Раша не противоречит исходной матрице ответов, а какие противоречат модели Раша.
Необходимо проверить при определенном уровне значимости α следующую нулевую статистическую гипотезу Ho: генеральная совокупность участников испытания и тестовых заданий такова, что вероятность  адекватно моделируется формулой Раша:
адекватно моделируется формулой Раша:
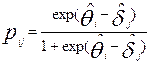
В качестве меры согласия теоретической и экспериментальной величины вероятности выбирают χ2 – критерий Пирсона:
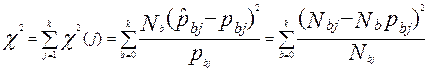 .
.
Число степеней свободы (ν) χ2 – распределения равно g-1, где g – количество групп, на которые разбиваются участники испытания в зависимости от набранного балла (g=K+1), таким образом, ν=K. Следует учесть, что число участников тестирования должно быть относительно велико. Статистика  имеет K(K+1) число степеней свободы.
имеет K(K+1) число степеней свободы.
Поскольку в условиях нулевой гипотезы статистика χ2 должна иметь определенное конкретное вероятностное распределение, то появляется возможность сравнить наблюдаемое значение  и критическое
и критическое  (взятое из соответствующих таблиц для χ2 распределения).
(взятое из соответствующих таблиц для χ2 распределения).
Если  ≥
≥  , то модель Раша не согласуется с опытными данными.
, то модель Раша не согласуется с опытными данными.
Если  ≤
≤  , то модель Раша согласуется с опытными данными.
, то модель Раша согласуется с опытными данными.
При проведении тестирования возникает необходимость обработки матрицы ответов, состоящей из элементов аij принимающих случайные значения 0 (неправильно) или 1(правильно). Математическое ожидание и дисперсия будут соответственно равны:
 ,
,  ,
,
где i=1, 2, 3, ……..N (N-число участников тестирования), j=1, 2, 3, …….K (К-число заданий в тесте),  - вероятность правильного решения i- участником с уровнем подготовленности
- вероятность правильного решения i- участником с уровнем подготовленности  задания j с уровнем трудности
задания j с уровнем трудности  .
.
 ,
, 
Статистические оценки 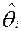 и
и 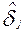 , математическое ожидание и дисперсии уровней подготовленности участников тестирования и уровней трудности заданий позволяют вычислить нормированное уклонение (ν(аij)) элемента аij матрицы ответов:
, математическое ожидание и дисперсии уровней подготовленности участников тестирования и уровней трудности заданий позволяют вычислить нормированное уклонение (ν(аij)) элемента аij матрицы ответов:
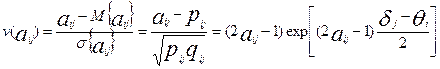 .
.
Согласно модели Раша для 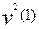 и
и 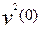 получим:
получим:
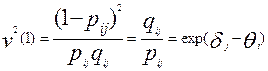 ,
,
 ,
,
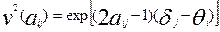 .
.
Если сумма квадратов указанных нормированных уклонений для всех значений аij матрицы ответов составляющих единую строку (ответы i- участника на все задания) или единый столбец (ответы всех участников на j-задание) подчиняются распределению χ2 , то модель Раша применима к результатам данного тестирования. Иными словами должны выполняться следующие равенства:
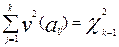 ,
,  ,
,
где K-1 и N-1 соответствующее число степеней свободы нормированного уклонения. На практике 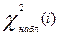 и
и 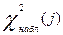 рассчитывают, используя следующие выражения:
рассчитывают, используя следующие выражения:
 ,
,
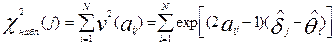 .
.
Если вычисления значения критерия 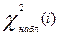 или
или 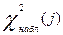 не превосходят критических значений при заданном уровне значимости α и соответствующем числе степеней свободы, то можно считать, что анализируемая строка или столбец полученных результатов не противоречит модели Раша и следовательно, эта модель применима. Более подробную информацию по данному вопросу можно найти в работе [13].
не превосходят критических значений при заданном уровне значимости α и соответствующем числе степеней свободы, то можно считать, что анализируемая строка или столбец полученных результатов не противоречит модели Раша и следовательно, эта модель применима. Более подробную информацию по данному вопросу можно найти в работе [13].
Проверка равномерности распределения дистракторов и эффективности их работы
Дистракторы являются очень важным элементом тестовых заданий в закрытой форме, с выбором одного или нескольких правильных ответов. При этом остальные ответы не являясь правильными должны выглядеть правдоподобными (их принято называть дистракторами). Оказывается, что при удачном подборе дистракторов, испытуемые, неправильно отвечающие на задание выбирают их с одинаковой частотой. Равномерность распределения дистракторов является показателем надежности и валидности задания. Рассмотрим следующий пример расчета равномерности распределения дистракторов [6]. Пусть, на какое то из заданий теста, содержащее 5 вариантов ответов, 642 человека дали неправильные ответы. Теоретическая частота выбора каждого из дистракторов составляет 642/4=160,5. Составим следующую таблицу 1:
Таблица 1
| Частоты | Номер дистрактора | Σ | |||
| 1 | 2 | 3 | 4 | ||
| Экспериментальная частота выбора (n) | 140 | 179 | 180 | 143 | 642 |
| Теоретическая частота выбора (n*) | 160,5 | 160,5 | 160,5 | 160,5 | 642 |
| (n-n*) | -20,5 | 18,5 | 19,5 | -17,5 | 0 |
Для  получим:
получим: 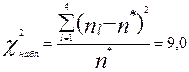 . Критическое значение критерия, соответствующее трем степеням свободы и уровню значимости α=0,05
. Критическое значение критерия, соответствующее трем степеням свободы и уровню значимости α=0,05  . Поскольку,
. Поскольку, 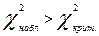 , то гипотезу о равномерном выборе дистракторов следует отвергнуть, однако при α=0,02
, то гипотезу о равномерном выборе дистракторов следует отвергнуть, однако при α=0,02 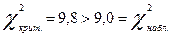 .
.
Анализ выбора дистракторов данным испытуемым может представлять не менее важную задачу, чем анализ равномерности распределения. Поскольку, он позволяет в ряде случаев выявить характер “незнания” тестируемого и составить представления о мере эклектичности его знаний.
Для оценки равномерности распределения дистракторов, а по существу определения эффективности их работы могут быть использованы отличные от определения 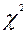 коэффициента подходы. В частности можно использовать подход [14], основанный на модели Раша, согласно которой вероятность
коэффициента подходы. В частности можно использовать подход [14], основанный на модели Раша, согласно которой вероятность 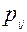 того, что i- участник тестирования с уровнем подготовленности
того, что i- участник тестирования с уровнем подготовленности  правильно выполнит j – задание с уровнем трудности
правильно выполнит j – задание с уровнем трудности  определяется формулой:
определяется формулой:
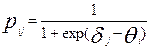 ,
,
а вероятность неправильного ответа 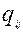 (выбора одного из дистракторов данного задания):
(выбора одного из дистракторов данного задания):
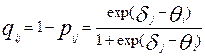 .
.
Предположим, что вероятность выбора одного из r – дистракторов ( 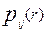 ), предлагаемых в данном тестовом задании, является монотонно убывающей функцией уровня подготовленности участника, и линейно связанна с вероятностью
), предлагаемых в данном тестовом задании, является монотонно убывающей функцией уровня подготовленности участника, и линейно связанна с вероятностью 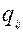 неправильного ответа, например:
неправильного ответа, например:
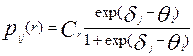 ,
,
где 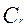 некоторый коэффициент линейной связи. Нахождение значения коэффициента
некоторый коэффициент линейной связи. Нахождение значения коэффициента  при использовании выборок испытуемых порядка нескольких тысяч человек в сравнении с результатами работы дистракторов, полученными другими методами, показывает, что величина
при использовании выборок испытуемых порядка нескольких тысяч человек в сравнении с результатами работы дистракторов, полученными другими методами, показывает, что величина  для хороших дистракторов варьируется от 0,98 до 1,02, а для плохих
для хороших дистракторов варьируется от 0,98 до 1,02, а для плохих 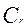 < 0,90. При этом наблюдается очень хорошее согласование результатов, что показывает возможность использования коэффициента
< 0,90. При этом наблюдается очень хорошее согласование результатов, что показывает возможность использования коэффициента 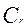 для оценки работы дистракторов.
для оценки работы дистракторов.
Дата добавления: 2019-01-14; просмотров: 343; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
