Десятичная запись приближенных чисел. Значащая цифра. Верные значащие цифры. Округление чисел. Связь между числом верных знаков и погрешностью числа

⇐ ПредыдущаяСтр 3 из 8Следующая ⇒

Десятичная запись приближенных чисел. Значащая цифра. Верные значащие цифры. Известно, что любое положительное число a может быть представлено в виде конечной или бесконечной десятичной дроби

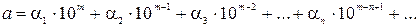где α_i – цифры числа (i = 1, 2, 3,…, n, …), причем α_i ≠ 0, а m – старший десятичный разряд числа a. Каждая единица соответствующего i – го разряда, если считать слева направо, имеет свое значение 10^m ^-ⁿ ^{+ 1}, называемое ценой разряда. Так, цена первого (слева) разряда есть 10^m , второго - 10^m ^{– 1} и т. д.

Например, в десятичной записи числа 2857,697

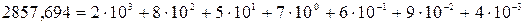цена разряда, в котором стоит цифра 8, есть 10^{3- 2 + 1} = 100; цифра 7 –

10^{3- 4 + 1}=1, цифра 4 - 10^{3- 7 + 1} = 0,001.

На практике обычно имеют дело с приближенными числами, представляющими собой конечные десятичные дроби

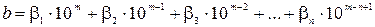Все сохраняемые десятичные знаки β_i (i = 1, 2, 3,…, n) называются значащими цифрами числа b, причем возможно, что некоторые из них равны нулю (за исключением β₁). При позиционном отображении числа b в десятичной системе счисления нередко приходится вводить лишние нули в начале или в конце числа, например

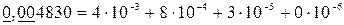
или

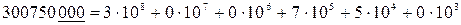Такие нули (в приведенных примерах они подчеркнуты) не считаются значащими числами.

Определение 1. Значащей цифрой приближенного числа называются всякая цифра, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда. Все остальные нули, входящие в состав приближенного числа и служащие лишь для обозначения десятичных разрядов его других цифр, не причисляются к значащим цифрам.

У Данилиной А.И. [1] дается несколько иное определение. Значащими цифрами называются все его цифры, кроме нулей, стоящих левее первой отличной от нуля цифры.

Нули в конце числа – всегда значащие цифры (в противном случае их не пишут). Например, числа 0,00207 и 54,700 имеют соответственно 3 и 5 значащих цифр.

При написании целых чисел могут иметь место некоторые тонкости. Так, если мы хотим показать, что у выше написанного числа 300750000 последние три нуля не являются значащими, то используется нормализованная форма записи чисел: 0,300750·10⁹. Число 0,00207 в этой форме запишется в виде 0,207·10^-2. В этих записях 0,300750 и 0,207 – мантиссы соответствующих чисел, 9 и -2 – порядки чисел.

Определение 2. n первых значащих цифр приближенного числа являются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого n – й значащей цифрой (α_n), считая слева направо, т. е. выполняется неравенство

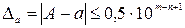. (2)

Например, для точного числа A = 47,96 число a = 48,00 является приближением с тремя верными знаками, так как 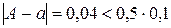(здесь m =1; n = 3).

Если неравенство (2) не выполняется, то цифру α_n называют сомнительной.

У Копченовой Н.В. [3] приводится более простое правило определения числа верных знаков приближенного числа.

Количество верных знаков числа отсчитывается от первой значащей цифры числа до первой значащей цифры его абсолютной погрешности; например, число a = 20,7626 с абсолютной погрешностью Δ_a = 0,0926 имеет три верных знака (2, 0, 7); остальные знаки сомнительные. В приближенном числе a = 15, 00235, имеющему абсолютную погрешность Δ_a = 0,1·10^-3, имеется пять верных знака (1, 5, 0, 0, 2).

Замечание. При выполнении неравенства (2) количество верных значащих цифр понимается в узком смысле. Наряду с таким понятием используется понятие верных значащих цифр в широком смысле.

Число a является приближением точного числа A с n верными знаками в широком смысле, если абсолютная погрешность 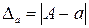не превышает единицы десятичного разряда, в котором стоит n-я значащая цифра α_n приближенного числа, т. е. выполняется неравенство

. (3)

Например, для точного числа A = 457,9678 число a = 457,967 является приближением с шестью верными знаками, так как 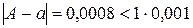(здесь m =2; n = 6).

Округление чисел. Часто возникает необходимость в округлении приближенного или точного числа a, т. е. в замене его числом a₁ с меньшим количеством значащих цифр. При этом сохраняют одну или несколько цифр, считая слева направо, и отбрасывают все последующие. Число a₁ выбирают так, чтобы погрешность округления 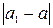была минимальной.

Наиболее употребительными являются следующие правила округления.

1. Если отбрасываемые цифры составляет число, большее половины единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу.

2. Если отбрасываемые цифры составляет число, меньшее половины единицы последнего оставляемого разряда, то оставляемые цифры не изменяются.

3. Если отбрасываемые цифры составляет число, равное половине единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу, если она нечетная, и остается без изменения, если она четная (правило четной цифры).

Примеры. Округлить до трех цифр следующие числа:

а) a = 13,8658. Согласно правилу 1, получим a₁ = 13,9;

б) a = 148,358. Согласно правилу 2, получим a₁ = 148;

в) a = 6,86500. Согласно правилу 3, получим a₁ = 6,86;

г) a = 347,50. Согласно правилу 3, получим a₁ = 348;

д) округляя число π = 3,1415926535… до пяти, четырех и трех значащих цифр, получим приближенные числа 3,1416; 3,142; 3,14 с абсолютными погрешностями, меньшими 0,5·10^-4; 0,5·10^-3; 0,5·10^-2.

Точность приближенного числа зависит не от количества значащих цифр, а от количества верных значащих цифр. В случаях, когда приближенное число содержит излишнее количество неверных значащих цифр, прибегают к округлению. При этом руководствуются следующим практическим правилом:

При выполнении приближенных вычислений число значащих цифр промежуточных результатов не должно превышать числа верных цифр более чем на одну или две единицы. Окончательный результат может содержать не более чем одну излишнюю значащую цифру, по сравнению с верными.

Заметим, что абсолютная погрешность приближенного числа a₁ после округления складывается из абсолютной погрешности числа a и погрешности округления

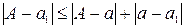Связь между числом верных знаков и относительной погрешностью приближенного числа. Устанавливается на основе следующей теоремы (доказательство приведено в [2, с. 25-27]).

Теорема. Если положительное приближенное число a имеет n верных цифр в узком смысле, то относительная погрешность δ этого числа не превосходит 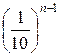, деленную на первую значащую цифру α₁ данного числа,

т. е. .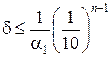

Из этой теоремы вытекают два следствия.

Следствие 1. За предельную относительную погрешность числа a можно принять:

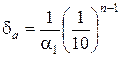, (4)

где α₁ - первая значащая цифра числа a.

Следствие 2. Если число a имеет больше двух верных цифр т. е. n ≥ 2, то справедлива формула

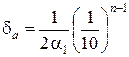. (5)

Замечание. Если приближенное число a имеет n верных цифр в широком смысле, то оценки (4) и (5) следует увеличить в два раза.

Пример 1. Какова относительная погрешность, если вместо числа π взять число a = 3,14?

Решение. В данном примере α₁ = 3 и n = 3. Следовательно

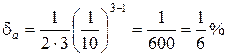Пример 2. Сколько десятичных знаков взять при вычислении 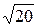с относительной погрешностью 0,1%?

Решение. Так как первая цифра результата 4, т. е. α₁ = 4, а δ_a = 0,001, то согласно , имеем 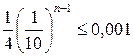. Из последнего неравенства находим 10 ⁿ^-1≥250 и n ≥ 4.

Вышеприведенная теорема дает возможность по числу верных знаков приближенного числа

(6)

определить его относительную погрешность δ.

Из формулы относительной погрешности 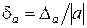имеем

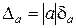. (7)

Учитывая старший десятичный разряд Δ_a, легко установить количество верных знаков данного приближенного числа a. В частности, если

то из формул (6) и (7) находим

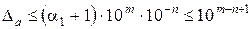т. е. число a имеет n верных цифр в широком смысле. Аналогично, если

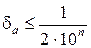То число a имеет n верных цифр в узком смысле.

Пример 3. Приближенное число a = 24253 имеет относительную точность 1%. Сколько в нем верных цифр?

Решение. Имеем

Δ_a = 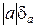=24253·0,01≈243=2,43·10².

Следовательно, число a имеет верными только первые две цифры (n = 2); цифра сотен является сомнительной. Согласно приведенному в определении 1 правилу, число a предпочтительнее записать в виде a = 2,43·10⁴.

3. Погрешности суммы и разности. Потеря точности при вычитании близких чисел [1]

Погрешность суммы. Рассмотрим точные числа A₁, A₂,…, A_n и их приближенные значения a₁, a₂,…, a_n. Пусть 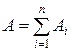- сумма всех точных чисел, а 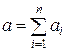- сумма их приближенных значений и известны абсолютные погрешности , ,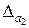…, 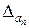всех приближенных чисел. Необходимо оценить абсолютную погрешность суммы приближенных чисел.

Составим разность

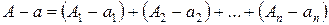Переходя к абсолютным величинам правой и левой частей записанного выражения и используя свойство абсолютных величин, получим

, т. е.

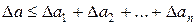. (8)

Следствие. За абсолютную погрешность алгебраической суммы приближенных чисел можно принять сумму абсолютных погрешностей этих чисел

. (9)

Из последней формулы следует, абсолютная погрешность суммы не может быть меньше абсолютной погрешности наименее точного слагаемого. Поэтому не имеет смысла сохранять излишние знаки и в более точных слагаемых. Отсюда при сложении чисел различной абсолютной точности поступают следующим образом:

1) выделяют число (или числа), имеющее наибольшую абсолютную погрешность;

2) остальные числа округляют по образцу выделенных, сохраняя один запасной десятичный знак;

3) производят сложение чисел, учитывая все сохраненных знаки;

4) полученный результат округляют на один знак.

Пример. Найти сумму приближенных чисел: 345,4; 0,348; 0,1834; 235,2; 11,75; 9,27; 0,0849; 0,0214; 0,000354, каждое из которых имеет все верные значащие цифры (в широком смысле).

Решение. 1) Выделяем числа наименьшей точности 345, 4 и 235,2, абсолютная погрешность которых может достигать 0,1.

2) Округляем остальные числа с точностью до 0,01: 0,35; 0,18; …;

3) Выполняя суммирование всех полученных чисел, получим

345,4

235,5

11,75

9,27

0,35

0,18

0,08

0,02

0,00

602,25

Округляя результат до 0,1 по правилу четной цифры, находим приближенное значение суммы 602,2.

Полная погрешность Δ результата складывается из трех слагаемых:

1) суммы погрешностей исходных данных

Δ₁ = 1·10^-1+ 1·10^-3+ 1·10^-4+ 1·10^-1+ 1·10^-2+ 1·10^-2+ 1·10^-4+ 1·10^-4+ 1·10^-6 =

= 0,221301< 0,222;

2) абсолютной величины суммы ошибок (с учетом их знаков) округления слагаемых

Δ₂ = | - 0,002 + 0,0034 + 0,0049 + 0,0014 + 0,000354 | =

= 0, 008054< 0,009;

3) ошибки округления результата суммирования чисел

Δ₃ = 0,050.

Следовательно,

Δ = Δ₁ + Δ₂ + Δ₃ ≤ 0,222 + 0,009 + 0,050 = 0,281< 0,3;

и, таким образом, искомая сумма составляет 602,2 ± 0,3.

Запишем без доказательства следующую теорему

Теорема. Если слагаемые – одного и того же знака, то относительная погрешность их суммы не превышает наибольшей из относительных погрешностей слагаемых, т. е.

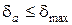Пример можно выполнить на основе предыдущей задачи по аналогии как это сделано в [1].

Погрешность разности. Рассмотрим разность двух приближенных чисел 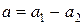. Согласно формуле (9), абсолютная погрешность разности равна сумме абсолютных погрешностей уменьшаемого и вычитаемого

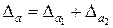Следовательно, относительная погрешность разности составляет

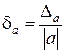. (10)

Замечание. Если приближенные числа a₁ и a₂ достаточно близки друг к другу по своим значениям и имеют малые абсолютные погрешности, то число a мало. Из (10) вытекает, что относительная погрешность может быть весьма большой, в то время относительные погрешности уменьшаемого и вычитаемого остаются малыми, т. е. происходит потеря точности. В этом случае используют следующее правило.

При приближенных вычислениях следует избегать вычитания почти равных приближенных чисел. В некоторых случаях это можно добиться путем предварительного преобразования выражения a₁ - a₂. Если это не удается, то следует уменьшаемое и вычитаемое брать с достаточным числом запасных верных знаков (если такая возможность имеется). Например, если известно, что при вычитании чисел a₁ и a₂ первые m значащих цифр их пропадут, а результат необходимо иметь с n верными значащими цифрами, то следует взять a₁ и a₂ с m + n верными значащими цифрами.

Дата добавления: 2019-01-14; просмотров: 2031; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!