Моделирование процессов в исследуемой системе

Стр 1 из 3Следующая ⇒

ЛАБОРАТОРНАЯ РАБОТА № 1 АНАЛИЗ ДИНАМИКИ ИМПУЛЬСНОЙ СИСТЕМЫ I. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ Изучение способов построения математической модели линейной импульсной системы; анализ устойчивости; расчет переходных процессов; экспериментальное исследование простейших импульсных САУ. II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Структурная схема простейшей линейной системы представлена на рис.1. f e e* у Рис. 1. При описании линейных импульсных систем наибольшее распространение получили Z - передаточные функции, представляющие собой отношение Z-преобразования выходной величины к Z -преобразованию входной величины. Так Z-передаточная функция W(z) разомкнутой системы, соответствующей рис.1, определится так: . Z-передаточная функция замкнутой системы определяется выражением: . Ключевым моментом при математическом описании линейной импульсной системы является определение Z-передаточной функции разомкнутой системы, представленной на рис. 2. e e* у Рис. 2. Для такой схемы Z-передаточная функция, как правило, определяется как результат применения -преобразования к передаточной функции W(p) приведенной непрерывной части, т.е. . Приведем таблицу -преобразования для некоторых функций W(p). Так как -преобразование обладает свойством линейности, то в случае, если W(p) - сложное дробно-рациональное выражение, вычисление соответствующей Z-передаточной функции можно проводить в следующей последовательности: 1. Передаточную функцию W(p) разложить на простейшие дроби: W(p)=W1(p)+W2(p)+...+ Wr(P) 2. Для каждой простейшей дроби Wi(p), из таблицы найти -преобразова-ние, т.е. , . 3. С учетом теоремы линейности -преобразования можно записать записать W(z)=W1(z)+W2(z)+... + Wr(z). Рассмотрим случай, когда в состав непрерывной части системы входит экстраполятор нулевого порядка, т.е. , где , - дробно-рациональная функция. Тогда . и, так как в соответствии со свойствами -преобразования множитель может быть вынесен за знак -преобразования, то . Здесь под знаком -преобразования стоит дробно - рациональная функция. Определив , используя разложение на простейшие дроби, можно найти Z-передаточную функцию разомкнутой системы. Пусть ПНЧ содержит в качестве формирующего звена экстраполятор нулевого порядка. Тогда передаточную функцию ПНЧ можно представить в виде . В этом случае для определения Z-передаточной функции можно использовать зависимость , где s1, s2, ...s к - полюсы функции Wi(s). Передаточная функция замкнутой системы, изображенной на рис. 1, определяется по формуле . где W(z) - передаточная функция разомкнутой системы. Устойчивость линейной системы с передаточной функцией Ф(z) зависит от значений корней соответствующего характеристического уравнения. Пусть , C(z) и D(z) - многочлены. Тогда уравнение D(z) = 0 будет характеристическим уравнением импульсной системы и для устойчивости импульсной системы необходимо и достаточно, чтобы: 1. все корни уравнения удовлетворяли условию , n - степень D(z) 2. корни с единичными модулями были простыми. Для решения вопроса об устойчивости в простейшем случае можно просто решить характеристическое уравнение. В данной работе так и нужно делать. Если система имеет высокий порядок, следует использовать критерии устойчивости. Рассмотрим построение переходного процесса в импульсной системе. Положим для простоты начальные условия нулевыми. Тогда, зная входной сигнал f(t) и соответствующую функцию f(kt), найдем Выходная величина определится по формуле обратного Z-преобразования . Полученное таким образом выражение задает аналитическую зависимость у от дискретного аргумента k. Методику численного расчета процессов в импульсной САУ проиллюстрируем на примере. Пусть передаточная функция Ф(z) имеет вид . Перейдем к разностному уравнению, связывающему выходную и входную переменные. Имеем . Умножению изображения на z при нулевых начальных условиях соответствует смещение на такт аргумента оригинала. С учетом этого получим уравнение . Решая его численно, получим процесс на выходе системы y[kt]. III. ОБЪЕКТ ИССЛЕДОВАНИЯ, ПРИБОРЫ, ОБОРУДОВАНИЕ ОБЪЕКТ ИССЛЕДОВАНИЯ – система, структурная схема которой приведена на рис. 3. АИЭ f e u y - Рис. 3. Здесь Т1 = Т = 1с , k = 4. В работе используется система MATLAB, с помощью которой моделируется данная система. ПРИБОРЫ, ОБОРУДОВАНИЕ – персональный компьютер IBM PC. IV. ЗАДАНИЕ НА РАБОТУ Получить математическое описание системы: Z-передаточные функции разомкнутой и замкнутой системы, разностное уравнение, связывающее вход f и выход у системы; провести исследование устойчивости и определить диапазон значений К j, соответствующих устойчивости САУ; построить переходный процесс; провести численное исследование системы. V. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Расчетная часть

1. Составить структурную схему системы, раскрыв АИЭ как последовательное соединение ИИЭ и экстраполятора нулевого порядка.

2. Записать в общем виде Z-передаточную функцию разомкнутой САУ.

3. Записать выражение для передаточной функции замкнутой системы.

4. Вычислить Z--передаточную функцию замкнутой САУ, считая коэффициенты K₁ , K₂ параметрами системы.

5. Определить требования, накладываемые на коэффициенты K₁ , K₂ из условия устойчивости САУ. При заданном k = 4 найти диапазон значений коэффициента K₂ , соответствующий устойчивости системы и максимально возможное значение K₂_kp.

6. При K₁=10, f(t)=l(t), K₂= a K₂_kp (a задается преподавателем) рассчитать переходный процесс, получив аналитические зависимости для выхода системы.

7. Записать разностное уравнение дискретной системы относительно y[kt], f[kt] и провести его численное решение.

Моделирование процессов в исследуемой системе

1. Составить схему моделирования исследуемой системы в среде SIMULINK под управлением MATLAB. С этой целью выполнить следующие действия:

1.1. Запустить пакет SimuLink.

1.2. Открыть раздел библиотеки SimuLink с источниками сигналов ( Source ), нажав на соответствующую пиктограмму в окне «Library».

1.3. Выбрать указателем «мышки» источник постоянного входного сигнала («Constant») и перенести его копию в поле моделирования (окно «untitled», которое пока не имеет своего названия).

1.4. Аналогичными действиями перенести в поле моделирования блоки, необходимые для формирования заданной структуры:

из раздела «математика» ( Math ):

a) сумматор;

b) апериодическое звено;

c) безинерционное звено (коэффициент передачи обратной связи).

из раздела «дискретные элементы» ( Diskrete ):

d) экстраполятор нулевого порядка ( Zero-Order Hold).

из раздела «приемники» ( Sinks ):

e) осциллограф (Scope) для просмотра результатов моделирования.

1.5. Расположить блоки в соответствии с их местом в исследуемой системе. Перемещение блоков осуществляется установкой указателя «мышки» на соответствующий блок и захватом его путем нажатия правой кнопки «мышки». Далее блок перемещается в нужном направлении. При занятии им желаемого места в поле моделирования правая кнопка «мышки» отпускается.

1.6. Связать установленные блоки моделирования между собой. С этой целью указатель «мышки» устанавливается на вход элемента, при этом в нужном месте появляется перекрестье. Далее, нажав правую кнопки «мышки», ведут линию к выходу элемента, являющегося источником сигнала для рассматриваемого блока. Перечисленные действия повторяют для всех блоков системы. В результате выполнения данного пункта из разрозненных блоков формируется единая система.

1.7. Установить параметры блоков, входящих в систему:

Общий алгоритм установки параметров простейших блоков заключается в следующем:

• указатель «мышки» устанавливается на соответствующий блок;

• выделение блока осуществляется двойным щелчком правой кнопки мыши. Выполнение указанных манипуляций приведет к раскрытию окна параметров выделенного блока;

• редактирование соответствующих параметров блока;

• закрыть окно параметров блока путем «нажатия» кнопки Close.

Схема моделирования дискретной системы представлена на рис.4.

Рис.5.

2. Изменяя коэффициент передачи K₂ , определить его критическое значение, соответствующее границе устойчивости системы K_2к_p (критическому значению K₂ соответствует возникновение незатухающих колебаний в САУ). Зарисовать колебания, существующие в системе.

3. Установить значение K₂ =aK_2к_p , получить и зарисовать переходный процесс на выходе системы, соответствующий f(t)=l(t).

VI. ОФОРМЛЕНИЕ ОТЧЕТА

В отчете должны быть представлены структурная схема дискретной САУ, процесс получения передаточных функций и их выражения, величина K_2к_p , уравнение дискретной системы, теоретические переходные процессы, схема моделирования дискретной САУ, вид незатухающих колебаний и значение K_2к_p , экспериментальный переходный процесс.

VII. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое Z- передаточная функция и как ее можно получить?

2. Как оценить устойчивость системы?

3. Как строятся переходные процессы в системе?

4. Как определить устойчивость системы по виду наблюдаемых в ней процессов?

ЛАБОРАТОРНАЯ РАБОТА № 2

АНАЛИЗ УСТОЙЧИВОСТИ И КАЧЕСТВА ПРОЦЕССОВ
В ИМПУЛЬСНОЙ СИСТЕМЕ

I. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ

Изучение особенностей анализа устойчивости линейной импульсной системы; оценка влияния параметров САУ на качество переходных процессов; экспериментальное исследование системы.

2.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Составной частью данной работы является получение Z-передаточных функций разомкнутой и замкнутой систем. Однако здесь рассматривается более сложная САУ, имеющая внутренние обратные связи, поэтому при выводе передаточной функции замкнутой системы целесообразно воспользоваться общим алгоритмом получения Z-передаточных функции линейных импульсных систем. Напомним его. Для получения эквивалентной передаточной функции сложного соединения необходимо:

1. Ввести вспомогательные переменные, приняв за них сигналы на входах ИИЭ.

2. Связать вспомогательные переменные, входную и выходную переменные между собой, используя Z-передаточные функции. В итоге получится система уравнений относительно изображений вспомогательных, входной и выходной переменных.

3. Исключить изображения вспомогательных переменных и записать уравнение, связывающее изображение входа и выхода.

4. Записать эквивалентную передаточную функцию системы.

В данной работе проводится анализ устойчивости системы и D-разбиение по двум ее параметрам. Напомним, что для того, чтобы система была устойчивой, необходимо и достаточно выполнение условия

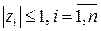, (1)

где z_i - корни характеристического уравнения. При этом корни с единичным модулем должны быть простыми.

Запишем характеристическое уравнение

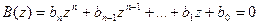. (2)

При проведении D-разбиения коэффициенты b ₀ , b _1; ...., b _n оказываются зависящими от параметров, по которым оно выполняется. Из условия (1) определяются требования, по которым должны удовлетворять коэффициенты b ₀ , b _1; ...., b _n, чтобы система была устойчивой, и далее формируются требования к параметрам системы. Однако на практике этот путь применим только к системам 1-го порядка. При необходимости применения D-разбиения для системы второго порядка имеет смысл предварительно преобразовать уравнение (2) так, чтобы можно было использовать критерии устойчивости непрерывных систем. Проведем замену переменных

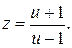(3)

Это преобразование переводит единичную окружность комплексной плоскости 'z' в мнимую ось Re u = 0 плоскости 'u'. Внутренняя часть окружности 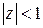преобразуется в левую полуплоскость плоскости 'u', а внешняя её часть - в правую полуплоскость плоскости 'u' . Характеристическое уравнение (2) принимает вид

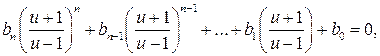
или. после преобразований

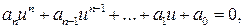(4)

где каждый из коэффициентов 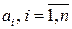линейно зависит от коэффициентов b ₀ , b _1; ...., b _n . Очевидно, что условие устойчивости имеет вид

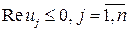и к уравнению (4) могут быть применены известные алгебраические критерии устойчивости, на основании которых и формулируются требования к параметрам D-разбиения. Для систем 2-го порядка уравнение имеет вид

a ₂ u ² + a ₁ u + a ₀ =0 ,

и необходимые и достаточные условия устойчивости принимают форму неравенств

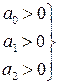(5)

Если а₀, а₁, а₂ зависят от параметров, по которым проводится D-разбиение, то данная система неравенств и определяет область значений параметров, соответствующих устойчивой импульсной системе.

В лабораторной работе для исследуемой системе требуется определить коэффициенты, при которых имеет место так называемый процесс конечной деятельности. Дело в том, что в импульсной системе можно добиться того, чтобы свободные процессы заканчивались за n тактов ( n - порядок системы), после чего устанавливается вынужденный процесс. Такие процессы называются процессами конечной длительности. Для их возникновения нужно, чтобы коэффициенты характеристического уравнения системы

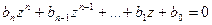
удовлетворяли условиям

b ₀ = b ₁ =…= b_n _-1 = 0 .

При этом характеристическое уравнение принимает вид

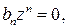
а его корни равны нулю. Для системы второго порядка с характеристическим уравнением

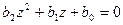
условия возникновения процессов конечной длительности имеют вид]

b₀ = b₁= 0 .

Выполнение этих условий можно обеспечить подбором двух параметров системы, входящих в выражения для коэффициентов b₀ , b₁.

III. ОБЪЕКТ ИССЛЕДОВАНИЯ, ПРИБОРЫ, ОБОРУДОВАНИЕ.

ОБЪЕКТ ИССЛЕДОВАНИЯ – система, структурная схема которой приведена на рис. 1.

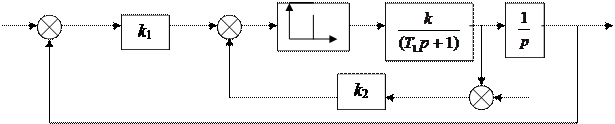f e e e ^* ^y

- -

f ( t )

Рис. 1.

Здесь Т₁=Т=1с , k =6.

В процессе работы система моделируется на персональном компьютере с использованием пакета MATLAB.

ПРИБОРЫ, ОБОРУДОВАНИЕ – персональный компьютер IBM PC.

IV. ЗАДАНИЕ НА РАБОТУ

1. Получить передаточную функцию замкнутой системы .

2. На плоскости коэффициентов k_1,k₂ выделить область их значений, соответствующую устойчивой системе.

3. Определить значение коэффициентов k_1,k₂ , обеспечивающих в системе процессы конечной длительности.

4. Провести численное определение области устойчивости по параметрам k_1,k₂ и исследование процессов конечной длительности.

V. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

Расчетная часть

1. Составить структурную схему САУ, раскрыв АИЭ как последовательное соединение ИИЭ и экстраполятора.

2. Пользуясь изложенным выше алгоритмом, получить выражение для
Z-передаточной функции замкнутой системы Ф(z).

3. Определить входящие в выражение для Ф(z) передаточные функции разомкнутых частей системы и подставив их в зависимость для Ф(z), получить передаточную функцию замкнутой системы, считая k_1,k₂ параметрами, значения которых еще не определены.

4. Провести анализ устойчивости в следующем порядке:

• записать характеристический многочлен системы;

• провести преобразование (3) и получить характеристическое уравнение в виде (4). При этом коэффициенты а₀ ¸ a₂ будут функциями k_1,k₂;

• используя условия (5), на плоскости k_1,k₂ выделить область значений коэффициентов, соответствующих устойчивости системы;

• при значении k₁ , заданном преподавателем, определить величину k₂, соответствующую двукратному запасу устойчивости по амплитуде.

5. Определить значение коэффициентов k₁⁰_, k₂⁰,обеспечивающие существование процессов длительности. Рассчитать процесс конечной длительности при .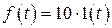

Дата добавления: 2019-01-14; просмотров: 188; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!