Численное дифференцирование и интегрирование
Цифровая вычислительная машина может обрабатывать непрерывный сигнал только как последовательность дискретных значений. Методы приближений можно применять для дифференцирования и интегрирования дискретных данных.
Полиномом в конечных разностях называется полиноминальная функция, которая проходит через заданное число конечных точек. Он аналогичен разложению в ряд Тейлора, которое обеспечивает совпадение с заданным числом производных функций.
При рассмотрении конечно-разностных полиномов используются следующие обозначения:
Хr - значение Х в момент времени tr содержащееся в памяти машины,
Хr+n - значение Х в момент времени tr + nh, содержащееся в памяти машины,
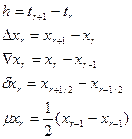
Операторы ∆, µ, δ,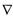 
можно применять к выражениям последовательно. Применение операторов. иллюстрируется следующим примером:
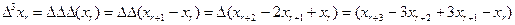
При работе управляющей вычислительной машины часто приходится дифференцировать и интегрировать данные. Чтобы это оказалось возможным, мы должны иметь непрерывное представление данных. Это достигается построением конечно-разностного полинома, проходящего через заданное число точек. Приведем пример конечно-разностного полинома:
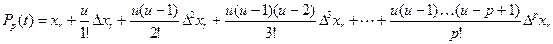
где 
Соответствующий конечно-разностный полином третьей степени может быть записан в виде:
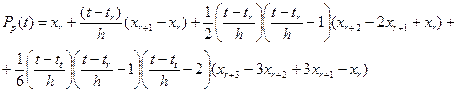
Проверка показывает, что конечно-разностный полином P3 совпадает с непрерывным сигналом x в дискретных точках t = tr , t = tr + h, t = tr + 2 h и t = tr + 3 h
|
|
|
Дифференцирование
Конечно-разностную формулу дифференцирования можно получить дифференцированием соответствующего конечно-разностного полинома по t. Например, дифференцирование предыдущей формулы дает:
Полагая в t = tr получаем
Если исходить из других конечно-разностных полиномов, можно получить другие конечно-разностные формулы дифференцирования. Приведем еще один пример, в котором используются центральные разности:
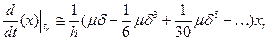
Интегрирование
Конечно-разностные формулы для численного интегрирования можно получить аналогичным путем. Рассмотрим, например, полином
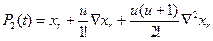
где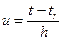 
(Убедитесь в том, что Р2(t) в дискретных точках t = tr., t = tr -h и t = tr - 2h совпадает с Х.)
Формулу интегрирования можно получить аналитически:
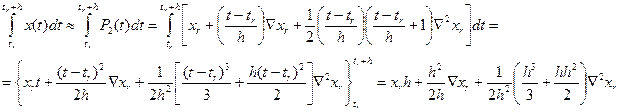
Если исходить из конечно-разностного полинома Стирлинга, то может быть выведена следующая формула интегрирования:
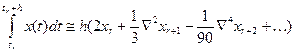
Следует отметить, что первые два члена описывает известное правило Симпсона для отыскания площади под кривой.
Естественно, чем больше членов содержит конечно-разностная схема, тем лучшим оказывается приближение к непрерывным данным и, следовательно, более точной формула интегрирования или дифференцирования. Первые отброшенные члены в этих выражениях обычно хорошо оценивают ошибку усечения.
|
|
|
Дата добавления: 2018-11-24; просмотров: 126; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!