Минимальное формализованное представление для непрерывной системы
Уравнение состояния и передаточная функция
При любых видах управляющих устройств объект как правило непрерывный.
Понятие цифрового управления часто используется в смысле управления в дискретные моменты времени каким-либо объектом, хотя, строго говоря, термин «цифровое управление» означает управление движением объекта цифровой вычислительной машиной с присущим ей эффектом дискретизации. При этом показатели эффективности и качества управления оцениваются по характеру движения системы в непрерывной временной области. Следовательно, объект системы цифрового управления можно рассматривать как непрерывную во времени систему.
Уравнение для выходной переменной формализовано представляется в виде
, 
, 
, 
, 
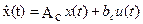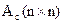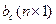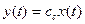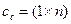(1.26)
где х(t) - n-мерный вектор переменных состояния, u(t) - входное воздействие, у(t) - выходная координата. Параметры bс, Сc для многомерных систем имеют вид матриц соответствующих размерностей, например Вс(n × m), Сс(р × n).
Применим прео6разование Лапласа к системе уравнений (1.26).
Обозначим такое преобразование функции x(t) как F+1{x(t)} = X(s). Тогда преобразование Лапласа производной этой функции будет иметь вид
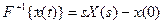
В результате преобразования Лапласа обеих частей уравнения получим
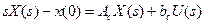
Это дает нам возможность представить систему уравнений на комплексной плоскости S в виде
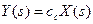
Здесь U(s), Y(s) -- преобразование Лапласа соответственно для функций u(t), у(t) (в случае многомерных систем преобразование Лапласа векторных функций осуществляется покомпонентно). Принимая х(0) = 0, из приведенных выше выражений получим
|
|
|
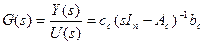
Отношение называется передаточной функцией непрерывной системы. Преобразовав обратную матрицу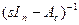 
в выражении, можно переписать передаточную функцию в виде
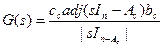
Выражение представляет собой правильную рациональную дробь, степень полинома знаменателя которой больше либо равна степени полинома числителя. Система с такой передаточной функцией называется собственной, или характеристической, системой. Корни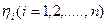 
полинома знаменателя передаточной функции
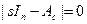
или, другими словами, собственные (характеристические) числа матрицы Ас, называются полюсами системы, а корни полинома числителя
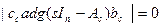
нулями системы. Вводя понятие системной передаточной матрицы Mс(S) вида
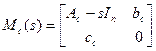
можно отметить, что нули передаточной функции (2.5) совпадают с нулями полинома I
.
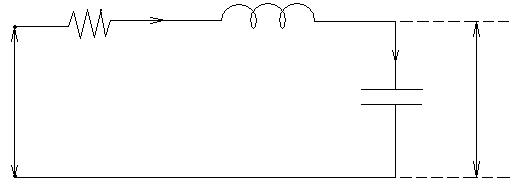
Пример 1.3. Пусть имеется электрическая цепь, состоящая из последовательно соединенных элементов: катушки индуктивности L, конденсатора емкостью С и активного сопротивления R. Падения напряжения на элементах такой электрической цепи v(t) и ток в контуре i(t) подчиняются зависимостям
|
|
|
, 
, 
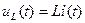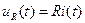(1.27)
Исходя из зависимостей (1.27) и закона Кирхгофа можно получить уравнение состояния для данной системы. Для этого, приняв за переменные состояния ток, протекающий через катушку индуктивности , и напряжение на обкладках конденсатора и обозначив ток в катушке индуктивности через Х1 (t), а напряжение на обкладках конденсатора через Х2(t), запишем уравнение баланса напряжений в виде
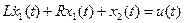(1.28)
где u(t) – напряжение на входе. Учитывая соотношение
C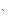 
x2(t) = x1(t) (1.29)
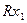
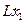
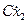
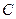
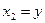
а)
 |
|
|
|
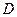
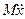
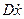
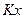
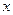
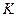
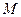
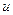
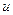
б)
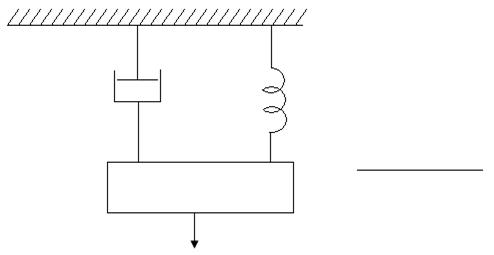
Рис 1.3. а) Электрический LCR контур, б)Пример механической системы
и приводя выражения (1.28) и (1.29) к нормальной форме Коши, получим уравнения состояния системы
и уравнение выхода системы
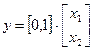
принимая в качестве выходной координаты напряжение на обкладках конденсатора
(У =Х2).
Передаточная функции системы, будет иметь вид
Пример 1.4. Пусть имеется механическая система, представляющая собой груз массой М, закрепленный на пружине с коэффициентом упругости К и движущийся в вязкой среде с коэффициентом вязкого трения D. Инерционная сила (fи), сила упругости (fу) и сила вязкого трения (fтр), действующие в системе, определяются соотношениями
, 
, 
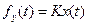где х(t)- перемещение груза.
Принимая u (t) за приложенную к грузу внешнюю силу (внешнее воздействие), запишем уравнение динамики системы
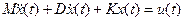
Обозначая перемещение х через Х1, а скорость перемещения х через Х2 и рассматривая их в качестве переменных состояния, на основании выражения (2) по аналогии с предыдущим примером получим уравнение состояния механической системы в виде
|
|
|
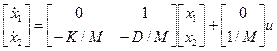
и уравнение выхода системы
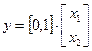
если в качестве выходной координаты у считать перемещение груза X1.
Минимальное формализованное представление для непрерывной системы
Рассмотрим обратную задачу получения уравнения состояния и уравнения выхода системы с минимальным числом n переменных состояния по известной передаточной функции или импульсной переходной характеристике данной системы. Такая задача в общем виде получила название задачи минимального представления системы.
Известны два основных способа получения уравнения состояния системы по ее передаточной функции. Первый способ применим в случае, когда заданная передаточная функция не содержит кратных полюсов. Тогда, представляя передаточную функцию в виде суммы простейших дробей, получим выражение
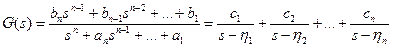
позволяющее определить искомые коэффициенты уравнения состояния Ас, bс, Сс:
, 
, 
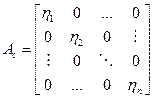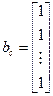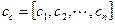
Такое представление получило название диагональной канонической формы представления. При этом параметры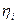 
, сi могут быть как действительными, так и комплексными. Прикладные вопросы использования этого способа, например для разработки электрических схем, достаточно подробно рассмотрены в работе.
Если заданная передаточная функция содержит кратные полюса, то применяется второй способ, согласно которому коэффициенты полиномов числителя и знаменателя исходной передаточной функции непосредственно участвуют в формировании матриц
, 
, 
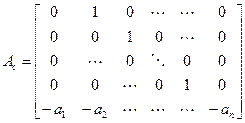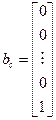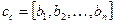
Такое представление получило название управляемой канонической формы представления.
Проиллюстрируем вышеизложенное следующим примером.
Пример 1.5 Пусть задана передаточная функция вида
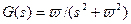
Вычисляя корни полинома знаменателя, это выражение можно представить как сумму простейших дробей
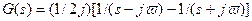
С использованием диагональной канонической формы представления требуемое минимальное представление в этом случае будет иметь вид
, 
, 
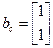а с использованием управляемой канонической формы представления минимальное представление- получим в виде
, 
, 
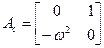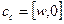
Дата добавления: 2018-11-24; просмотров: 425; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!