Расстояние от точки до прямой.
Пусть прямая l задана общим уравнением Ах + Ву + С = 0 и задана точка М*(х*,у*). Рассмотрим точку М0(x0, y0), лежащую на прямой l. Значит Ах0 + Ву0 + С = 0 или С= – Ах0 – Ву0. Тогда вектор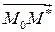 
(х*–х0, у*–у0).
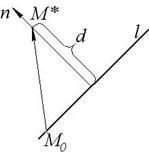
Рис. 3.1. Расстояние от точки до прямой
Расстояние до прямой (рис.3.1).
d=|прn |=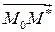 
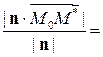
d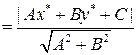 
(3.19)
Пример 3.3.
Найти расстояние от точки А (7, –3) до прямой, заданной уравнением
3х + 4у + 15 = 0.
Решение.
А² + B² = 9 + 16 = 25, d =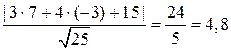 
.
Взаимное расположение прямых.
Если прямые l1 и l2заданы общими уравнениями А1х + В1у + С1 = 0 и А2х + В2у + С2 = 0, то
1) если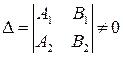 
, то прямые пересекаются;
2) если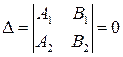 
, но 
или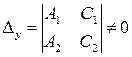 
, то прямые параллельны;
3) если 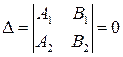и 
, 
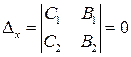, то прямые совпадают.
Прямая и плоскость в пространстве
Отметим, что многие утверждения и формулы, касающиеся плоскости в пространстве, доказываются и выводятся так же, как при изучении прямой на плоскости, поэтому в этих случаях будут даваться ссылки на предыдущий материал.
3.3.1. Плоскость в пространстве.
Получим сначала уравнение плоскости, проходящей через точку М0(х0, у0, z0) перпендикулярно вектору n = (A , B , C), называемому нормалью к плоскости. Для любой точки плоскости М(х, у, z) вектор
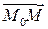= (x – x0, y – y0, z – z0) ортогонален вектору n, следовательно, их скалярное произведение равно нулю:
A(x – x0) + B(y – y0) + C(z – z0) = 0. (3.20)
|
|
|
Получено уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору.
После приведения подобных можно записать уравнение (3.20) в виде:
Ax + By + Cz + D = 0, (3.21)
где D = –Ax0– By0 – Cz0.
Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.
Неполные уравнения плоскости.
Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение (3.21) называют неполным.
Рассмотрим возможные виды неполных уравнений:
1) D = 0 – плоскость Ax + By + Cz = 0 проходит через начало координат.
Пример 3.4.
Постройте плоскость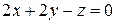 
.
Решение. При z=0 в плоскости Oxy получим уравнение прямой y = -x, также легко выяснить, что плоскость проходит через точку (0, 1, 2). Тогда плоскость имеет вид (рис. 3.2).
Рис. 3.2. Плоскость, проходящая через начало координат
2) А = 0 – n=(0,B , C)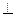 
Ox, следовательно, плоскость By + Cz + D = 0 параллельна оси Ох.
3) В = 0 – плоскость Ax + Cz + D = 0 параллельна оси Оу.
Пример 3.5.
Постройте плоскость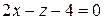 
.
Решение.
Заданная плоскость параллельна оси Oy, так как B = 0. В плоскости Oxz получим уравнение прямой z = 2x-4. Тогда плоскость имеет вид (рис. 3.3).
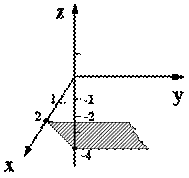
Рис. 4.3. Плоскость параллельная оси Oy
|
|
|
4) С = 0 – плоскость Ax + By + D = 0 параллельна оси О z .
5) А = В = 0 – плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох и Оу).
6) А = С = 0 – плоскость Ву + D = 0 параллельна координатной плоскости Ох z.
Пример 3.6.
Постройте плоскость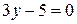 
.
Рис. 3.4. Плоскость параллельная плоскости Oyz
7) B = C = 0 – плоскость Ax + D = 0 параллельна координатной плоскости Оу z (рис. 3.4).
8) А = D = 0 – плоскость By + Cz = 0 проходит через ось Ох.
9) B = D = 0 – плоскость Ах + С z = 0 проходит через ось Оу.
10) C = D = 0 – плоскость Ax + By = 0 проходит через ось Oz.
11) A = B = D = 0 – уравнение С z = 0 задает координатную плоскость Оху.
12) A = C = D = 0 – получаем Ву = 0 – уравнение координатной плоскости Ох z.
13) B = C = D = 0 – плоскость Ах = 0 является координатной плоскостью Оу z.
Если же общее уравнение плоскости является полным (то есть ни один из коэффициентов не равен нулю), его можно привести к виду:
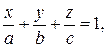(3.22)
называемому уравнением плоскости в отрезках. Способ преобразования показан в предыдущем разделе. Параметры а, b и с равны длинам отрезков, отсекаемых плоскостью на координатных осях.
Пример 3.7.
|
|
|
Постройте плоскость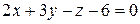 
.
Решение.
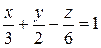. То есть а = 3, b = 2 и с = –6.
Рис. 3.5. Уравнение плоскости в отрезках
Замечание: подчеркнем, что плоскость тянется бесконечно во все стороны за нарисованные линии, ограничивающие треугольник.
Дата добавления: 2018-11-24; просмотров: 309; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!