Дифференциальное уравнение упруго-изогнутой оси балки
ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ
Кафедра теоретической и прикладной механики
Секция сопротивление материалов
УДК 539.–3
РАСШИРЕННЫЙ ЭЛЕКТРОННЫЙ КОНСПЕКТ
ЛЕКЦИЙ ПО КУРСУ
«сопротивление материалов»
для самостоятельной работы студентов в
условиях кредитно-модульной системы с
образовательно-квалификационным уровнем
«БАКАЛАВР»
2 часть (весенний семестр)
направление подготовки 0921 «СТРОИТЕЛЬСТВО»
для специальностей:
6.092100 «Промышленное и гражданское строительство»,
6.092100 «Городское строительство и хозяйство»,
6.092100 «Технология строительных конструкций изделий и
материалов»,
6.092100 «Строительство и эксплуатация автомобильных
дорог и аэродромов»,
6.092100 «Теплогазоснабжение и вентиляция»,
6.092600 «Водоснабжение и водоотведение»,
6.070800 «Экология».
АВТОРЫ:
Профессор Мущанов В. Ф.
Профессор Шевченко Ф. Л.
Доцент Осыка В. И.
Доцент Демидов А. И.
Макеевка 2006 г.
Содержание
Часть
МОДУЛЬ 9. ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ БАЛОК. 3
9.1. Основные понятия. 3
9.2. Дифференциальное уравнение упруго-изогнутой оси балки. 4
9.3. Метод непосредственного интегрирования при определении перемещений в балках. Граничные условия. 5
9.4. Метод начальных параметров определения перемещений при изгибе балок постоянной жесткости. 7
|
|
|
9.5. Энергетический метод определения перемещений в упругих системах. 13
9.6. Статически неопределимые балки. 22
Модуль 10. СЛОЖНОЕ СОПРОТИВЛЕНИЕ. 26
10.1. Общие понятия. 26
10.2. Сложный (неплоский) изгиб. 26
10.3. Изгиб с растяжением (сжатием) 32
10.4. Изгиб с кручением. Расчет круглого вала. 38
МОДУЛЬ 11. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ И УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ 40
11.1. Продольно-поперечный изгиб. 40
11.2. Устойчивость сжатых стержней. 41
11.3. Формула Эйлера. 42
11.4. Границы применимости формулы Эйлера. 46
11.5. Практический расчет сжатых стержней. 47
МОДУЛЬ 12. ДИНАМИЧЕСКОЕ ВОЗДЕЙТВИЕ НАГРУЗКИ.. 51
12.1. Учет сил инерции. 51
12.2. Приближенный динамический расчет упругих систем с распределенными параметрами 52
12.3. Собственные колебания упругих систем.. 53
12.4. Гармонические и ударные нагрузки при поперечных колебаниях. 55
12.5. Продольные колебания и удар. 57
МОДУЛЬ 13. РАСЧЕТ ТОНКОСТЕННЫХ ОБОЛОЧЕК. 59
13.1. Понятие о моментной и безмоментной теории расчета сосудов. 59
13.2. Расчет тонкостенных оболочек по безмоментной теории. 60
13.3. Частные случаи напряженного состояния оболочек. 62
Модуль 14. ПОНЯТИЕ О КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ.. 66
14.1. Общие понятия о концентрации напряжений. 66
14.2 Проверка прочности с учетом местных напряжений. 68
|
|
|
МОДУЛЬ 15. Колебания упругих систем.. 72
15.1. Колебания систем с одной степенью свободы.. 72
15.2. Собственные незатухающие колебания. 74
15.3. Собственные затухающие колебания. 78
15.4. Вынужденные колебания без учета сопротивления движению.. 79
15.5. Ударные нагрузки. 81
15.6. Вынужденные колебания при гармонических нагрузках. 83
15.7. Колебания систем с двумя степенями свободы.. 85
15.8. Поперечные колебания систем с распределенными параметрами. 87
15.9. Собственные колебания весомых балок. 88
15.10. Вычисление спектра частот собственных колебаний. 89
15.11. Метод начальных параметров в колебаниях балок. 90
15.12. Учет сосредоточенных масс в колебаниях весомых балок. 91
15.13. Учет гармонической нагрузки в весомых балках. 93
ЛИТЕРАТУРА. 95
МОДУЛЬ 9. ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ БАЛОК
Основные понятия
Ранее были рассмотрены вопросы, связанные с исследованием напряженного состояния балок при действии на неё внешних нагрузок. При этом основное внимание было уделено рассмотрению условий, при которых обеспечивается несущая способность балок.
Однако этого недостаточно, чтобы дать полную оценку работы балок под нагрузкой. Балки должны удовлетворять не только условиям прочности, но и условиям жесткости, т.е. при действии на них внешних нагрузок они должны не допускать чрезмерных перемещений.
|
|
|
При расчете строительных конструкций допустимые перемещения регламентируются строительными нормами на проектирование. Таким образом, чтобы выполнить расчеты на жесткость следует научиться определять перемещения, возникающие в балках. Кроме того, как известно, при раскрытии статической неопределимости систем составляются дополнительные уравнения, связывающие между собой перемещения. Следовательно, возникает вторая необходимость определения перемещений.
Какие же перемещения возникают в балках? Какая взаимосвязь существует между ними? Какие зависимости существуют между перемещениями и внутренними усилиями. Каким образом их определить? В дальнейшем нам с вами предстоит ответить на все поставленные здесь вопросы.
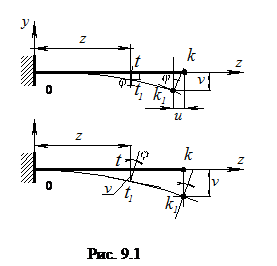
Рассмотрим некоторую балку в виде консоли, загруженную силой Р (рис.9.1), связанную с системой координатных осей zoy. При действии этой силы продольная ось балки изогнется, т.е. центры тяжести сечения переместятся на величину u по направлению оси z и на величину v по направлению оси y, а поперечные сечения повернутся на угол φ.
|
|
|
Но составляющая u полного перемещения обычно значительно меньше вертикальной составляющей v, в дальнейшем называемой прогибом в балке. Поэтому составляющей u можно пренебречь и считать, что все точки оси балки перемещаются только по вертикали.
Таким образом, при изгибе балки будем задачи решать относительно двух функций – прогиба v(z) и углов поворота сечений φ(z) в балке, между которыми имеет место дифференциальная зависимость:
(9.1)
Существует несколько методов определения указанных перемещений. В дальнейшем остановимся на некоторых из них. Прежде всего, обратим внимание на метод непосредственного интегрирования дифференциального уравнения изогнутой оси балки.
Дифференциальное уравнение упруго-изогнутой оси балки
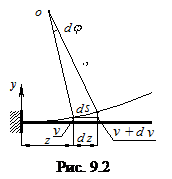Пусть в текущем сечении с координатой z прогиб равен v. В сечении с координатой z+dz его величина равна v+dv (рис.9.2). С одной стороны длина элемента дуги изогнутой оси балки
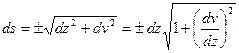(а)
С другой стороны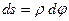 
, откуда получаем:
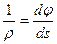(б)
Так как в соответствии с формулой (9.1) φ=arctg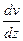 
, то
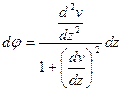(в)
Подставим в формулу (б) по формулам (в) и (а) значения dφ и ds получим выражение для кривизны изогнутой оси балки
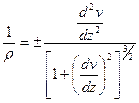(г)
Ранее при выводе формулы нормальных напряжений, была получена формула, связывающая кривизну оси балки с изгибающим моментом
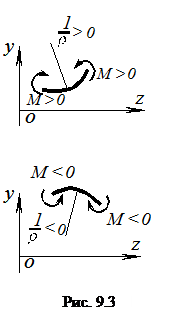
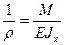(д)
Приравнивая согласно (г) и (д), получим
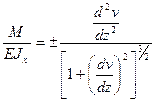(9.2)
Формула (9.2) называется точным дифференциальным уравнение изогнутой оси балки и может применяться при изучении перемещений в гибких балках. Решение такого уравнения представляет значительные математические трудности и выполняется с применением эллиптических функций.
В случае малых перемещений величина углового перемещения φ, как правило, составляет тысячные доли радиана. Поэтому в формуле (9.2) квадратом угла поворота по сравнению с единицей можно пренебречь. После этого структура уравнения (9.2) значительно упрощается и принимает вид:
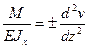(9.3)
Формула (9.3) содержит два знака «+» и «-». На рисунке (9.3) видно, что в принятой системе координат zoy положительной кривизне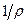 
оси балки соответствует положительный изгибающий момент, а отрицательной кривизне 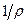оси балки соответствует отрицательный изгибающий момент М. Поэтому в формуле (9.3) следует сохранить только знак плюс. Если бы ось у была направлена вниз, тогда бы в формуле (9.3) следовало бы оставить знак минус. Таким образом, в дальнейшем будем использовать приближенное дифференциальное уравнение изогнутой оси балкив виде:
(9.4)
Дата добавления: 2018-11-24; просмотров: 315; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!