Нерекуррентный алгоритм идентификации.

  

 

Задача идентификации квазилинейного объекта заключается в определении коэффициентов разностного уравнения а _i и b_i по известным измерениям входного и выходного процессов u( k) и х( k) в дискретные моменты времени k:

u(0),u(1),…,u(k-1);

x(d+1),x(d+2),…,x(k+d).

Если учесть, что производится оценка параметров на k –м шаге изменений векторов U и X, то верно следующее:

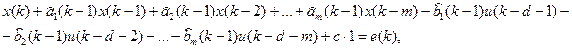
где 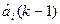,  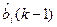- оценка i – х коэффициентов, полученная на предыдущем, ( k-1) - м шаге; e( k) – ошибка (невязка), полученная по причине неточного значения коэффициентов a_i, b_i, а также шумов измерения входного и выходного процессов U, X.

Данное уравнение можно представить как ошибку, определен­ную из разности действительного и спрогнозированного значений выходной координаты x( k):

e( k)= x( k)- x( k/( k-1)), где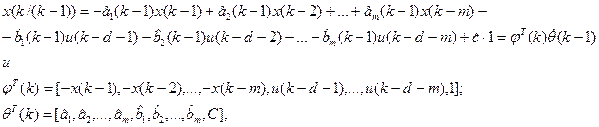

тогда

Использование матричных выражений позволяет представить взаимосвязь между параметрами и ошибками на шагах от ( m+ d-1) до ( m+ d+ N), т. е. на ( N+1)-м шаге. Рассмотрение ошибок и оце­нок на интервале в ( N+1)-й шаг позволяет перейти к средним оценкам и оптимальному выбору параметров из условия миними­зации этих ошибок.

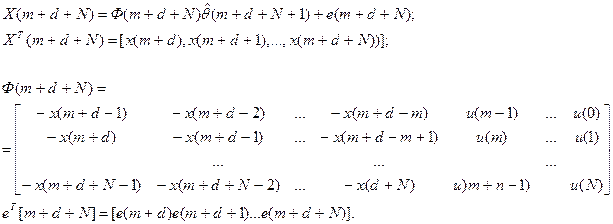
Вводя функцию потерь (ошибок):

произведем преобразования:

При определении минимума потерь (ошибок) исходим из необходимых условий:

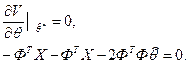
Отсюда:

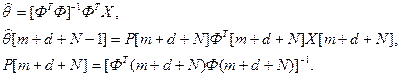 где

Недостатки нерекуррентного алгоритма.

1. Точность вычисления оценки может быть низкой из-за плохой обусловленности матрицы [Ф ^T(т + d + N)Ф( m + d + N)].

2. Велики затраты памяти машины.

3. Большой объем вычислений для определения оценки вектора параметров, препятствующий реализации алгоритма в темпе со временем.

 

Рекуррентный алгоритм идентификации.

  

 

Если ( k) и ( k + 1) - оценки на шагах k и ( k + 1) соответствен­но, то можно получить рекуррентную формулу для оценивания параметров системы:

Пусть проведено некоторое количество измерений, так что система содержит k скалярных уравнений. Запишем её в виде:

Проведя измерения в (k+1) -ый момент времени, получим

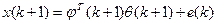 или в блочном виде:

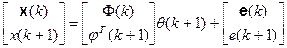
где индексы k и k+1, соответствующие q, показывают число уравнений в системе, которую для оценки q надо решить в смысле минимума среднеквадратической ошибки.

 

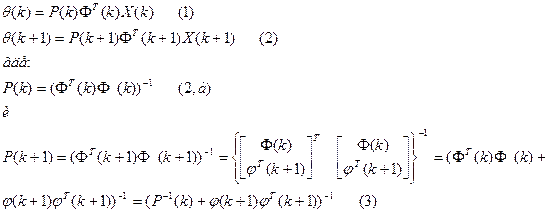
Переписывая (2), получаем:

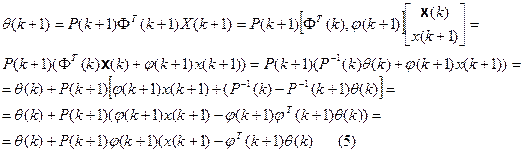
Формулы (4) и (5) позволяют вычислить новую оценку параметра q(k+1), если заданы предыдущая оценка q(k), оценка Р(k) и информация об , x(k) по измерениям в момент времени k. Для того чтобы можно было начать оценивание по рекурентной схеме,

Необходимо знать начальные значения q(0), Р(0). Матрицу Р(0) можно вычислить, воспользовавшись определением (2,а), а q(0)- из (1). Можно выбрать q(0) иначе (как чаще и делают) в соответствии с имеющейся априорной информацией, а в отсутствии такой информации q(0) полагают равным нулю:

q(0)=0

 Матрицу Р(0) в отсутствии априорной информации полагают пропорциональной единичной матрице

где 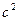 выбирается достаточно большим, так что влияние предложения, сделанного в (6), по мере учета в оценке новых измерений быстро становится пренебрежимо малым.

Итого:

P(0) = c² I, c→∞; I - единичная матрица; γ( k)- вектор коррекции;

 Приведенные формулы есть классические формулы идентифи­кации параметров по рекурентному методу наименьших квадратов. Однако для практического применения они, как правило, непосредственно не используются по следующей причине:

 Большое влияние точности вычислений на устойчивость оценки  - плохая обусловленность матриц.

Модифицированный алгоритм идентификации по методу квадратного корня.

Рекуррентный алгоритм целесообразно модифицировать, что­бы исключить непосредственные вычисления плохо обусловлен­ных матриц. Наибольшее распространение получил подход по ме­тоду квадратного корня [10]. Здесь используется переход от матри­цы Р( k) к матрице G( k), причем

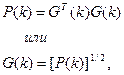
откуда следует:

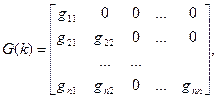
где G( k) - так называемая информационная матрица.

Воспользуясь выражением:

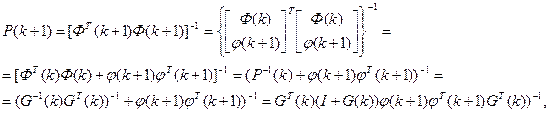
введем H( k) = G( k)φ( k + 1),

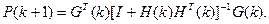
Отсюда:

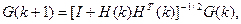
что позволяет вычислять G( k + 1) по значениям G( k).

Вектор коррекции:

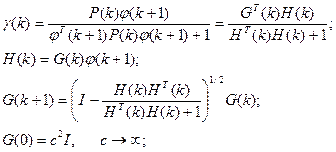
I - единичная матрица.

Вычисление квадратного корня в (2.15) производится по фор­муле Хелеского:

если N = V^TV, то:

- для диагональных элементов;

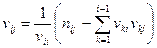- для недиагональных элементов.

По сравнению с классическим алгоритмом идентификации по методу наименьших квадратов модифицированный алгоритм идентификации по методу квадратного корня обладает большей устойчивостью благодаря меньшей вычислительной погрешности: он обеспечивает такую же точность, как классический алгоритм идентификации, при использовании ЭВМ с вдвое меньшей раз­рядностью центрального процессора.

Для целей сокращения операций в ЦВМ алгоритм имеет пошаговый вид:

 

 

---

Дата добавления: 2018-11-24; просмотров: 265; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!