ОПРЕДЕЛЕНИЕ, ПРИМЕРЫ, ПРОСТЕЙШИЕ СВОЙСТВА КОЛЕЦ.
Непустое множество К объектов произвольной природы называетя кольцом, если в нём выполнимы две бинарные алгебраические операции «+» и «*», удовлетворяющие следующим аксиомам:
1. "a,bÎK: a+b = b+a;
2. "a,b,cÎK: a+(b+c) = (a+b)+c;
3. $(Õ)ÎK, "aÎK: a+Õ = a;
4. "aÎK, $(-a)ÎK: a+(-a) = Õ;
Относительно операции «+» любое кольцо является абелевой группой.
5. "a,b,cÎK: a*(b+c) = a*b+a*c –левый дистрибутивный закон умножения относительно сложения;
"a,b,cÎK: (b+c)*a = b*a+c*a –правый дистрибутивный закон умножения относительно сложения;
Если выполняется 6.=>
6. "a,bÎK: a*b = b*a;
То кольцо К называется коммутативным кольцом.
В этом случае не разделяют левый и правый дистрибутивные законы умножения относительно сложения.
Если выполняется 7.=>
7. "a,b,cÎK: a*(b*c) = (a*b)*c;
То К называется ассоциативным кольцом.
Если выполняются 6. и 7., то К называют ассоциативно-коммутативным кольцом.
Если выполняется 8.=>
8. $ (1̃) , "aÎK: a*1̃ = 1̃*a = a;
То К называется кольцом с единицей(1̃).
Всё это обозначают как (К,+,*).
Справедливы следующие свойства колец:
Из выполнения аксиом 1.-4. следует, что любое кольцо образует аддитивную абелеву группу, поэтому все свойства абелевых групп справедливы в любом кольце.
1) $!(Õ) ÎК;
2) "aÎK , $!(-a)ÎК: a+(-a) = Õ;
В любом кольце выполняется операция вычитания, обратная операции сложения.
3) "a,bÎK: a+x = b имеет единственное решение x = b+(-a)
|
|
|
Обозначим b+(-a) = b-a –разность элементов b и a.
4) Из аксиомы ассоциативности (2.) операции сложения следует, что в любом кольце можно однозначно говорить о сумме любого конечного числа элементов из К.
5) В любом кольце справедливо свойство сократимости для операции сложения.
Т.е. "a,b,cÎK: a+b = a+c => b=c
Для доказательства достаточно к обеим частям равенства прибавить (-a).
6) В любом кольце "aÎK , (Õ)ÎК: a*Õ = Õ и Õ*a = Õ
Доказательство.
a*b=a*(b+Õ)=a*b+a*Õ
a*b= a*b+a*Õ => a*Õ = Õ
a*b= (Õ+a)*b= Õ*b+a*b => Õ*b= Õ
7) В любом кольце вводится понятие элемента кратного данному.
"aÎK: a+a+a+a+a+…+a = n*a , n из множества натуральных чисел. (n раз)
Если n=0, то 0*a= Õ
Если n<0, и n-целое число, то (-a)+(-a)+…+(-a)=n*a , где n<0
(-n раз)
7.1) "m,n ÎZ , "aÎK:
(n+m)*a = n*a+m*a
7.2) "n ÎZ , "a,bÎK :
n*(a+b) = n*a+n*b
7.3) "m,n ÎZ , "aÎK:
(n*m)*a = n*(m*a)
8) Справедливы правила знаков :
a*(-b)=-a*b
(-a)*b=-a*b
(-a)*(-b)=a*b
Доказательство.
a*b+a*(-b)=a*(b+(-b))=a*Õ=Õ=>a*(-b)=-a*b
Ч.Т.Д.
|
|
|
9) Справедливы дистрибутивные законы умножения относительно вычитания.
"a,b,cÎK: a*(b-c) = a*b-a*c
(b-c)*a=b*a-c*a
a*(b-c)=a*(b+(-c))=a*b+a*(-c)=a*b-a*c
10) Если взять любое n из множества натуральных чисел, то в кольце можно ввести понятие n-ой степени элемента, т.е.
Обозначим: a*a*a*…*a=a^n
(n раз)
Справедливы свойства степеней:
10.1) a^n*a^m=a^(n+m)
10.2) (a^n)^m=a^(n*m)
10.3) (a*b)^n=a^n*b^n
Примеры колец:
1- (Z,+,*), (Q,+,*), (R,+,*) – примеры числовых колец.
2- А={3n| n из Z} – ассоциативно-коммутативное кольцо без 1.
3- А={Õ}- пример простейшего кольца.
Õ выполняет в этом множестве и роль 0 и роль 1̃.
4- Пусть М- множество квадратных матриц n-го порядка с элементами из поля Р.
Это ассоциативное, но не коммутативное кольцо с 1.
5- P[x]- множество многочленов степени ≤n над полем Р.
Р[x]- ассоциативно- коммутативное кольцо с 1.
6- приведём пример нечислового кольца. Это кольцо классов вычетов по модулю m (mod m).
Кольцо классов вычетов по модулю m ( mod m ).
Определение. Два натуральных числа a и b, разность которых кратна натуральному числу m, называются сравнимыми по модулю m: a ≡ b (mod m).
|
|
|
Пусть дано множество Z, на котором введено бинарное отношение «быть сравнимым по mod m» - это отношение удовлетворяет свойствам рефлексивности, симметричности, транзитивности, а значит является отношением эквивалентности и делит множество Z на непересекающиеся классы. В один и тот же класс входят все целые числа сравнимые между
собой по mod m. Т.е. дающие при делении на m один и тот же остаток.
Т.к. при делении целых чисел на m может быть ровно m остатков 0,1,…m-1,то Z разбивается на m непересекающихся классов. Их называют классами вычетов по mod m.
Обозначим Z/m={0¯,1¯,2¯,…m-1¯¯}.
Покажем, что множество классов вычетов по mod m образует ассоциативно-коммутативное кольцо с 1.
Обозначим К=Z/m={0¯,1¯,2¯,…m-1¯¯}
Введём на множестве К операции сложения и умножения классов:
"a¯, b¯ÎК: a¯+ b¯=(a+b) ¯¯, но если a¯+ b¯≥m, то к числам a+b и m применяют теорему о делении с остатком
a+b=mq+r 0≤r≤m-1
a¯+ b¯=r ¯ , т.к. a+b≡r(mod m)
"a¯, b¯ÎК: a¯*b¯=(a*b) ¯¯, но если a*b≥m, то к числам a*b и m применяют теорему о делении с остатком
a*b=mq1+r1 0≤r1≤m-1
|
|
|
a¯*b¯=r 1¯
Покажем выполнимость аксиом кольца (1-8):
1) "a¯, b¯ÎК : a¯+ b¯=(a+b)¯¯=(b+a)¯¯= b¯+a¯- коммутативность.
2) "a¯, b¯, с¯ ÎК: a¯+(b¯+c¯) = (a¯+b¯)+c¯-ассоциативность.
3) $ нулевой элемент (0¯) "a¯ÎК: a¯+0¯ =(a+0)¯¯=a¯.
4) "a¯ÎК , $(m-a)¯¯ ÎК: a¯+(m-a)¯¯= (a+m-a)¯¯= m¯= 0¯.
(m-a)¯¯- противоположный класс для класса a¯,
1¯≤a¯≤(m-1)¯¯ |*(-1)
-1≥- a≥-(m-1)
-m+1≤- a≤-1
1≤m-a≤m-1
1¯≤(m-a)¯¯≤(m-1)¯¯
Докажем что (m-a)¯¯ принадлежит классу К:
5) Для любых a¯ и b¯ из К a¯*b¯=(a*b)¯¯=(b*a)¯¯= b¯*a¯.
6) Для любых a¯ , b¯ и с¯ из К a¯*(b¯*c¯) = (a¯*b¯)*c¯.
7) Существует единичный элемент (1¯) такой что для любого a из К: 1¯*a¯= (1*a)¯¯ = a¯.
8) Для любых a, b и c из К: a¯*(b¯+c¯) = a¯*b¯+a¯*c¯.
Таким образом множество классов вычетов по mod m образует ассоциативно-коммутативное кольцо с 1.
ПОДКОЛЬЦО. КРИТЕРИЙ ПОДКОЛЬЦА.
Пусть дано кольцо К. Непустое подмножество S кольца К называется подкольцом кольца К, если оно само образует кольцо относительно операций определённых в кольце К.
Справедлив критерий подкольца:
Для того что бы непустое подмножество S кольца К было подкольцом кольца К необходимо и достаточно что бы выполнялись 2 условия:
1. " a, b ÎS a-b так же принадлежит S
2. " a, b ÎS a*b так же принадлежит S
В некоторых источниках критерий подкольца формулируют так:
Для того что бы непустое подмножество S кольца К было подкольцом кольца К необходимо и достаточно что бы выполнялись 3 требования
1. " a, b ÎS a+b так же принадлежит S
2. " a ÎS $ (-a) так же принадлежащий S
3. " a, b ÎS a*b так же принадлежит S
Доказательство критерия(1):
1.необходимость. Дано: К-кольцо
S содержится в К
S непустое
S- подкольцо
Доказать выполнимость требований 1 и 2.
Т.к. S подкольцо кольца К, то S само образует кольцо относительно операций определённых в К. Выполнимость требований 1 и 2 вытекает из определения кольца и из свойств колец.
2.достаточность. Дано: К-кольцо
S содержится в К
S непустое
Доказать, что S- подкольцо кольца К.
Из выполнимости требований 1 и 2 следует что S- замкнуто относительно операции умножения. Что бы доказать, что S подкольцо кольца К, нужно показать что S замкнуто относительно операции сложения и выполняются аксиомы кольца.
Для любого a из S a-a принадлежит S по требованию 1,
но а-а=Õ => Õ принадлежит S - выполнилась аксиома 3.
Для любого а из S, Õ принадлежит S, тогда Õ-а принадлежит S по требованию 1, но Õ-а=-а => -a принадлежит S – выполнилась аксиома 4.
Возьмём любые a и b из S, тогда существует –b принадлежащее S, и тогда
a-(-b) принадлежит S по требованию 1. Но a-(-b)=a+b => a+b принадлежит S.
Т.е. S – замкнуто относительно операции сложения.
Выполнимость аксиом 1, 2, 5 в S следует из того, что S подмножество кольца К. Таким образом S – кольцо, а т.к. S содержится в К, то S подкольцо кольца К. Ч.Т.Д.
Замечание: Если кольцо К коммутативно или ассоциативно, то и любое его подкольцо коммутативно или ассоциативно.
Если кольцо К содержит 1, то его подкольцо S может 1 не содержать.
Примеры:
1. Любое кольцо для себя является подкольцом ( К содержится в К)
2. Подмножество состоящее из одного нулевого элемента кольца К есть подкольцо кольца К
Õ Î К, S={ Õ} – подкольцо кольца К.
Примеры 1 и 2 это примеры несобственных подколец кольца К.
Любое другое подкольцо кольца К, если оно есть , называется собственным подкольцом кольца К.
3. Z Ì Q Ì R Ì C
4. Дано (Z,+,*)
А={5n| n из Z}
А содержится в Z
A – подкольцо кольца Z без 1.
5. Дано С (комплексн.числа)
Z[i]={a+bi| a,b из Z, i²=-1}
Z[i] ÌС
Z[i] подкольцо кольца С
Воспользуемся критерием подкольца
"х1 ,х2 Î Z[i], х1=a+bi , x2=c+di , a,b,c,d Î Z.
1) найдём х1-х2=( a+bi)-( c+di)=(a-c)+(b-d)i, где a-c и b-d ÎZ, Þ х1-х2 Î Z[i]
2) найдём х1*х2=( a+bi)*( c+di)=(ac-bd)+(ad+bc)i, а так как ac-bd и ad+bc Î Z, Þ х1*х2 ÎZ[i]
Так как выполнились оба требования критерия, то Z[i] называется кольцом целых гауссовых чисел.
Делимость в кольцах. Свойства делимости.
Дано К- кольцо, оно замкнуто относительно операций сложения и умножения, в нём выполнима операция вычитание, обратная операции сложения, но К не замкнуто относительно операции деления.
Пусть даны любые a и b из К, где b≠0.
Говорят, что в кольце К элемент а делится на b≠0, если $qÎК: а=b*q, a кратно b.
Справедливы следующие свойства делимости:
1. "а ÎК, и а≠Õ: a кратно а – рефлексивность
а=а*1¯=> q=1¯
2. "а, b и с ÎК: Если (а кратно b) и (b кратно с) => (а кратно с) – транзитивность.
Т.к. (a кратно b) то существует q1 из К, а=b*q1
Т.к. (b кратно с) то существует q2 из К, b=c*q2
Тогда а=b*q1=(с*q2)*q1=c*(q2*q1), где q2*q1 принадлежит К => а кратно с
3. Если (a кратно b) и (с кратно b) =>(a±c) кратно b
4. Если (a кратно b) и (с не кратно b) =>(a±c) не кратно b
5. Если (а кратно b) и любое с из К => (ac) кратно b
6. "а Î К, и а≠Õ, Õ Î К, Õ кратно а, Õ=а*Õ => q=Õ
7. Существует 1̃ из К, для любого а из К, а кратно 1̃,
а=1̃*a => q=a.
Область целостности. Свойства делимости в области целостности.
Пусть дано ассоциативно- коммутативное кольцо К с единицей. Возьмём любые a и b из К, где b≠0. И пусть а кратно b. Это значит что существует q из К, такое что а=b*q.
В произвольно выбранном кольце элемент q может находиться не однозначно.
Пример:
К=Z/8={0¯,1¯,…7¯}
a=0¯, b=4¯
0¯=4¯*0¯, q=0¯
0¯=4¯*2¯, q=2¯
0¯=4¯*4¯, q=4¯
0¯=4¯*6¯, q=6¯
Во множестве колец особую роль играют такие кольца, в которых элемент q при делении a на b находится однозначно и его называют частным от деления a на b.
Определение. Элементы а и b кольца К называются делителями нуля в кольце К, если они оба отличны от нуля, а их произведение равно нулю.
Пример:
К=Z/8
4¯,2¯ принадлежат К
4¯≠0 , 2¯≠0
4¯*2¯=0¯
4¯*4¯=0¯
4 и 6 делители нуля в кольце К.
Определение. Ассоциативно- коммутативное кольцо с единицей без делителей нуля называется областью целостности.
В области целостности справедлива теорема (свойство сократимости):
Теорема. В области целостности для любых a, b и c из К, где а≠Õ, а*b=a*c => b=c
Доказательство.
Пусть в области целостности К при указанных условиях справедливо равенство ab=ac => ab-ac=Õ => a(b-c)=Õ и а≠Õ => b-c=Õ => b=c
Ч. Т.Д.
Следствие. В области целостности К: если а кратно b, где b≠Õ, существует единственный q из К, такой что a=b*q.
Доказательство.
Предположим, что на ряду с q $sÎК: а=b*s => bq=bs, а т.к. b≠Õ, то q=s – определяется однозначно.
В области целостности q называется частным от деления a на b (a кратно b), q=a/b.
Справедливо утверждение: В любой области целостности на 0 делить нельзя.
Доказательство.
Пусть дана область целостности К, для любых а и b из К, но b= Õ.
Предположим, что а кратно b, т.е. a кратно Õ => Существует q Î К: а= Õ*q, относительно элемента а есть две возможности: 1) а≠Õ В свойствах колец было доказано, что Õ*q=Õ => a=Õ, но одновременно a=Õ и а≠Õ быть не может => этот случай отпадает.
2) a=Õ, Õ= Õ*q, в этом случае элемент q неоднозначен, т.е. нарушается единственность частного q в области целостности К.
Следовательно в области целостности К на 0 делить нельзя.
Ч.Т.Д.
Обратимые элементы кольца.
Пусть дано ассоциативно- коммутативное кольцо К с 1.
Определение. Элемент e ÎК называется обратимым в К, если $e’ÎК : e*e’=1̃.
Принято элемент е’ обратный к элементу е обозначать е־¹
е*е־¹= е־¹*е=1̃
Из определения следует, что элемент е־¹ так же является обратимым элементом в кольце К.
Пример: К=Z
1 ÎZ , 1*1=1 , 1 – обратимый элемент в Z
-1 ÎZ, (-1)*(-1)=1, -1 – обратимый элемент в Z
1, -1 – обратимые элементы в Z
Пример : К=[i]={z | z=a+bi, a,b ÎZ, i²=-1}
"zÎZ[i], z=a+bi, a,b Î Z z≠0+0i
Найдем для z обратный- z־¹ : z*z־¹=1+0i
Предположим, что z־¹=с+di, c,dÎZ
Тогда z*z־¹=(a+bi)*(с+di)=1+0i
Найдём модули обеих частей последнего равенства, т.е. |(a+bi)*(с+di)|=|1|
|(a+bi)|*|(с+di)|=1
√(a²+b²)*√(c²+d²)=1
a²+b²>0
c²+d²>0
Последнее равенство возможно лишь тогда когда a²+b²=1 и c²+d²=1.
Если a²+b²=1 Þ
а=1, b=0 z=1+0i=1 a=0, b=1 z=0+1i=i
a=-1, b=0 z=-1+0i=-1 a=0, b=-1 z=0-1i=-i
Если c²+d²=1 Þ
Аналогично получим 1, -1, i, -i
1*1=1
(-1)*(-1)=1
i*(-i)=1
(-i)*i=1
Таким образом в Z[i] 4 обратимых элемента: 1, -1, i, -i.
Справедлива теорема: Множество обратимых элементов кольца образует мультипликативную группу.
Доказательство.
Обозначим через G – множество всех обратимых элементов кольца К:
G={ε,δ,γ,β,…} (G,*)
Выясним, будет ли операция «*» - бинарной алгебраической операцией на G
1. "ε,δ Î G, $ε ־¹,δ ־¹ Î К
ε*ε ־¹= ε ־¹*ε=1̃, δ*δ ־¹= δ ־¹*δ=1̃ => ε ־¹,δ ־¹ Î G.
Докажем, что ε*δ ÎG
1¯= 1¯* 1¯= (ε*ε ־¹ )*( δ*δ ־¹)=(ε*δ)*( ε ־¹*δ ־¹)=( ε*δ)*( ε*δ) ־¹=1
=> ( ε*δ)*( ε*δ) ־¹=1 => ε*δ ÎG.
Значит «*» - бинарная алгебраическая операция.
2. G – подмножество кольца К, а в кольце К операция «*» ассоциативна и коммутативна в G как на подмножестве К.
3. 1̃ Î G, т.к. 1̃*1̃=1̃
4. "ε ÎG, $ ε ־¹ ÎК : ε*ε ־¹=1̃=> ε ־¹ Î G (т.к. он также обратимый).
Таким образом множество обратимых элементов кольца К образует мультипликативную группу.
Ч.Т.Д.
Ассоциированные элементы кольца.
Пусть дано ассоциативно-коммутативное кольцо с 1.
Определение. Элементы а и b кольца К называются ассоциированными если существует обратимый элемент ε, такой что а*ε=b
(обозначается как а~b)
Пример: К=Z 1) 5ÎZ, 5=1*5, ε=1, 5~5
2)-5ÎZ, -5=(-1)*5, ε=-1, -5~5.
Пример: К=Р[x]
f(x)=3x-3
f(x)=3(x-1)
x-1=φ(x)
f(x)=3*φ(x) ε=3
f(x) ~ φ(x)
φ(x)=1/3(x) ε=1/3
φ(x) ~ f(x)
Справедлива теорема: Элементы а и b кольца К ассоциированы тогда и только тогда когда они делятся друг на друга.
Доказательство.
1.Необходимость. Дано: а,b из К, а~b
Доказать: (а кратно b) и (b кратно а)
Т.к. а~b => существует ε из К
а=b*ε, ε- обратим в К.
Т.к. а=b*ε => a кратно b
Т.к. ε- обратим, => существует ε ־¹ из К
Умножим обе части последнего равенства на ε ־¹ :
а*ε ־¹=b*ε*ε־¹
b=а*ε ־¹ => b кратно а
2.Достаточность. Дано: а,b из К, (а кратно b) и (b кратно а)
Доказать: а~b
Т.к. а кратно b, => $q ÎК, а=b*q
Т.к. b кратно а, => $ q1 ÎК, b=a*q1
а=b*q=(a*q1)*q=a*(q1*q), где q1*q ÎК => q1*q=1̃
Т.е. q1 и q обратимые.
а=q*b, q- обратимый => a~b.
Ч.Т.Д.
Идеалы кольца. Главные идеалы кольца и их свойства.
Пусть дана ассоциативно- коммутативное кольцо К с 1.
Непустое подмножетсво J кольца К, называется идеалом кольца, если выполняются 2 требования:
1) " а,bÎJ: a-b Î J
2) "а ÎJ и "r ÎК: а*r ÎJ.
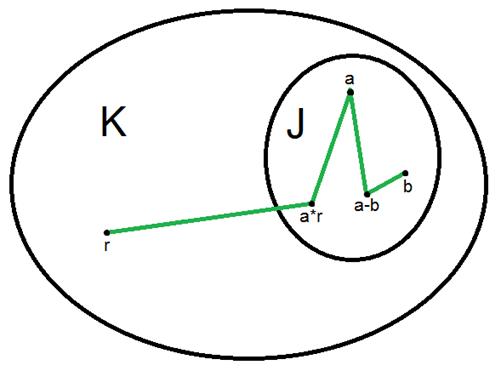
Заметим, что любой идеал кольца К является его подкольцом, но не любое подкольцо является идеалом.
Пример: Пусть дано подкольцо Z[i]={z| z=a+bi, a,b из Z, i²=-1}
Z содержится в Z[i]
Выясним будет ли Z идеалом:
1) "а ,b ÎZ, a-b Î Z – выполнилось 1ое требование идеала.
2) "а ÎZ и "r ÎZ[i], r=c+di
a*r=a*(c+di)=ac+adi Ï Z
ð Z не является идеалом в кольце К, но кольцо Z является подкольцом К.
Среди всех идеалов кольца К выделяют так называемые главные идеалы.
Определение. Главным идеалом кольца К, порождённым элементом а кольца К, называют множество элементов вида а*r, где r принадлежит К.
Обозначается (а).
(а)={ar| a ÎК, r Î К},
ar- элементы кратные а
К=Z, 5 Î Z,
(5)={5r| r из Z}={…, 5*(-3), 5*(-2), 5*(-1), 5*0, 5*1, 5*2, …}= {…, -15, -10, -5, 0, 5, 10, …}
-5 Î Z,
(-5)={ -5r| r ÎZ}={…, -5*(-3), -5*(-2), -5*(-1), -5*0, -5*1, -5*2, …}= {…, 15, 10, 5, 0, -5, -10, …}=(5)
(5)=(-5)
Заметим, что любой главный идеал кольца К является просто идеалом кольца К.
Свойства главных идеалов.
1. Любой главный идеал кольца К есть подкольцо кольца К.
Для доказательства достаточно применить критерий подкольца.
2. Порождающий элемент а принадлежит порождённому им главному идеалу. Т.е. а принадлежит (а).
Для доказательства достаточно в качестве элемента r выбрать единицу кольца К, т.е. r=1̃
a*r=a*1̃ принадлежит (а), а*1̃=а
а Î (а)
Ч.Т.Д.
3. Главный идеал, порождённый нулевым элементом состоит из одного нулевого элемента.
(Õ )={ Õ }
Доказательство.
Действительно, Õ принадлежит (Õ ), но Õ *r= Õ
(Õ )={ Õ *r| Õ ÎК, r ÎК}={ Õ }
Ч.Т.Д.
4. Главный идеал, порождённый единичным элементом, – есть всё кольцо К.
(1̃)={ 1̃*r| 1̃ Î К, r ÎК}=К.
Ч.Т.Д.
5. Если а кратно b => (a) Í (b)
Т.к. а кратно b => существует q из К , а=b*q
Для любого х из (а) => x=a*q1=b*(q*q1), где q*q1 ÎК.
х=b*(q*q1) => x Î (b)
Т.к. х выбирали произвольно => (а) Í(b).
6. (а кратно b) и (b кратно а) => (а)=(b)
Т.к. а кратно b => существует q из К : а=b*q
Для любого х из (а) => x=a*q1=b(q*q1) , где (а)Í(b), и q*q1 Î К.
Т.к. b кратно а => $ r ÎК , b=a*r
"х Î (b) => x=b*r1=a*(r*r1), где r*r1 ÎК.
ð (b) Í(а)
(а) Í(b)
(b) Í(а) Þ (а)=(b)
Ч.Т.Д.
Кольца главных идеалов. Евклидовы кольца.
Пусть дано ассоциативно- коммутативное кольцо К с 1.
Определение1. Кольцо К называется кольцом главных идеалов, если любой его идеал главный.
Определение2. Кольцо К называется Евклидовым кольцом если выполняются 2 условия:
1. "а Î К ставится в соответствие некоторое целое неотрицательное число:
а —> n(a), n(a) ÎZ, n(a)≥0
2. В К выполнима теорема о делении с остатком
"а и b ÎК, b≠0, $!q,r Î К:
а=bq+r, либо r= Õ , либо n(r)<n(b).
Пример. К=Z
1) "а ÎZ : а—>(а) n(a)=(a),
r=Õ, n(r)<n(b)
2) "а и b Î Z, b≠0, $!q,r ÎZ,
a=bq+r, 0≤r≤1.
Справедлива теорема:
Любое Евклидово кольцо является кольцом главных идеалов.
Доказательство.
Дано ассоциативно-коммутативное кольцо К, которое является Евклидовым кольцом. Выберем произвольным образом идеал J кольца К.
Заметим, что идеал J≠(Õ), потому что нулевой идеал уже является главным. Т.к. К- Евклидово кольцо, то любому элементу из К в частности любому элементу идеала J можно поставить в соответствие целое неотрицательное число.
Пусть b из J тот элемент идеала J для которого n(b) – наименьшее.
"а Î J, применим к элементам а и b теорему о делении с остатком: а=bq+r, r=0, либо n(r)<n(b), b≠0.
r=a-bq, т.к. а Î J, bq Î J => a-bq Î J => r Î J.
Относительно r есть две возможности:
r=Õ и r≠Õ
Если r≠Õ, тогда n(r)<n(b)
Пришли к противоречию, т.к. в идеале J нашёлся элемент r для которого n(r)<n(b), но b – это такой элемент идеала, для которого n(b) наименьшее.
ð r≠Õ быть не может, остаётся что r=Õ.
Тогда а=bq, где q принадлежит К, J=(b), т.к. а выбираем произвольно, то делаем вывод, что любой идеал J Евклидового кольца К, является главным идеалом. Следовательно Евклидово кольцо – является кольцом главных идеалов.
Ч.Т.Д.
Пример: Любой идеал кольца Z является главным.
Пример: Любой идеал кольца Р[x] является главным.
ГОМОМОРФИЗМ И ИЗОМОРФИЗМ КОЛЕЦ.
Пусть даны 2 кольца К и К’.
Определение. Два кольца К и К’ называются гомоморфными, если между ними можно установить такое однозначное отображение φ кольца К на кольцо К’ при котором для любых а и b из К и соответствующих им φ(а) и φ(b) из К, выполняются 2 условия:
1. φ(а+b)= φ(а)+ φ(b)
2. φ(а*b)= φ(а)* φ(b)
Если отображение φ будет взаимно- однозначным, то в этом случае кольцо К изоморфно кольцу К’:
Обозначается К 
К’ - гомоморфизм
К К’ - изоморфизм
Если кольца К и К’ изоморфны, то они и гомоморфны. Обратное не всегда верно. Что бы гомоморфные кольца были изоморфными, нужно что бы отображение φ было взаимно однозначным.
Пусть кольцо К гомоморфно кольцу К’, справедливы свойства гомоморфизма:
1) Нулю кольца К соответствует нуль кольца К’.
2) Противоположные элементы к соответствующим, соответствуют друг другу.
3) Если кольцо К коммутативное или ассоциативное, то и гомоморфное ему кольцо коммутативное или ассоциативное.
Заметим, что доказательство свойств 1-3 аналогично тому, как это делалось при доказательстве таких же свойств в теме группы.
Докажем 1ое свойство.
1. Возьмём любое а из К, и пусть а—>φ(а)=а’ принадлежащее К’
0 принадлежит К, 0—>φ(0)=b’ принадлежащее K’
a’=φ(a)=φ(a+0)=φ(a)+φ(0)=a’+b’
a’=a’+b’ => b’=0’ => φ(0)=0’
ч.ит.д.
Докажем 2ое свойство.
2. Возьмём любое а из К, и пусть а—>φ(а)=а’, φ(0)=0’,
Существует (-а) из К, а+(-а)=0
φ(-а)=с’, c’ принадлежит К
0’=φ(0)=φ(a+(-a))=φ(a)+φ(-a)=a’+c’
a’+c’=0’ => c’=-a’=-φ(a)
получили c’=-φ(a), т.е. φ(-a)=-a’
Пусть кольцо К изоморфно кольцу К’, справедливы следующие свойства изоморфных колец
1-3 справедливы.
4. К К’ - рефлексивность
| | |
5. К К’ => K’ K – симметричность
6. К1 К2 и К2 К3 => К1 К3 – транзитивность
Так как бинарное отношение «быть изоморфным», заданное на множестве колец, удовлетворяет свойствам рефлексивности, симметричности и транзитивности, то оно является отношением эквивалентности и разбивает множество всех колец на непересекающиеся классы изоморфных между собой колец.
Изоморфные кольца считаются с алгебраической точки зрения неразличимыми.
Что бы изучить целый класс изоморфных между собой колец, достаточно изучить все свойства одного кольца и перенести их на все свойства ему изоморфных, при условии, что при доказательствах использовались только свойства операций, а не индивидуальные свойства данного кольца.
Если доказано, что кольцо К изоморфно какому то множеству с двумя операциями «+» и «*», то это множество так же является кольцом.
Дата добавления: 2018-11-24; просмотров: 811; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!