Исследование устойчивости систем автоматического регулирования по алгебраическим критериям
Контрольная работа № 1
Типовые звенья систем автоматического регулирования
Цель работы: изучение типовых звеньев систем автоматического регулирования и построение частотных, временных и логарифмических характеристик.
Теоретическая часть
Звенья систем автоматического управления и регулирования различаются по виду их передаточной функции (или дифференциального уравнения), определяющей все их динамические свойства и характеристики. Основными типами звеньев являются: позиционные, дифференцирующие и интегрирующие.
Позиционными звеньями называются такие, передаточные функции которых имеют вид:
, 
,
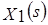
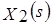где 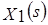- изображение по Лапласу сигнала на входе звена; 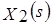- изображение по Лапласу сигнала на выходе звена; 
-коэффициент усиления звена; s -оператор Лапласа; многочлены 
и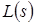 
имеют свободные члены, равные 1, то есть эти звенья обладают статической характеристикой 
(при 
), определяющей их состояние равновесия (свойство позиционности).
У дифференцирующих звеньев передаточная функция имеет вид
,
где 
имеет свободный член, равный 1. Для двукратно дифференцирующего звена числитель передаточной функции имеет вид 
.
Передаточные функции интегрирующих звеньев имеют соответственно вид:
или 
,
где 
имеет свободный член, равный 1.
Основными позиционными звеньями являются:
|
|
|
- идеальное усилительное звено
, 
;
- апериодическое звено первого порядка
, 
,
где 
- оператор дифференцирования;
- апериодическое звено второго порядка
, 
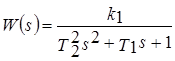, при 
;
- колебательное звено
, 
,
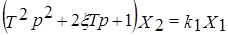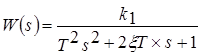где 
- коэффициент демпфирования, 
.
К интегрирующим звеньям относятся:
- идеальное интегрирующее звено
или 
, 
;
- инерциальное интегрирующее звено
, 
.
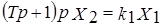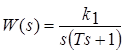К дифференцирующим звеньям относятся:
- идеальное дифференцирующее звено
, 
;
- форсирующее звено
, 
.
Основные характеристики звеньев
Амплитудно-фазовая частотная характеристика (АФЧХ) звена определяется
путем подстановки в операторную передаточную функцию звена 
(где 
- круговая частота, 
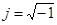) и выделении действительной и мнимой частей.
Например, для апериодического звена 1-го порядка получаем
Амплитудная частотная характеристика звена (АЧХ): 
.
Фазовая частотная характеристика звена (ФЧХ): 
.
В терминах MathCad указанные операции легко могут быть проведены следующим образом:
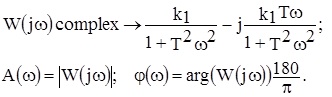
Логарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ):
.
|
|
|
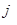
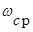
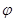
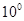
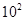
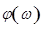
-45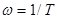 
-90
Рис.1. АФЧХ и ЛАФЧХ для апериодического звена 1-го порядка
Переходная и весовая функции звена
Переходной функцией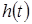 
называется реакция звена на единичное ступенчатое воздействие, то есть переходный процесс на выходе 
при единичном скачке на входе звена.
Следовательно,
, 
,
откуда переходная функция
.
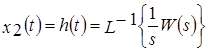Используя переходную характеристику, можно определить реакцию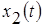 
на входное воздействие 
, заданное произвольной кривой при помощи интеграла Дюамеля
|
|
|
.
 |
1 
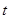
0 0
а) б)
Рис.2. График единичной ступенчатой функции (а) и
реакция типового колебательного звена (б)
Часто встречающимся воздействием на реальные системы являются кратковременные, но существенные по величине всплески, импульсы. Например, порывы ветра, ударная нагрузка и т. п. Моделирование подобного рода воздействий осуществляется с помощью единичной импульсной функции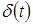 
, имеющей следующее определение
при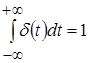 
.
Импульсная единичная функция относится к классу обобщенных функций и представляет собой производную от единичной ступенчатой функции:
.
Реакцию звена или системы на единичную импульсную функцию называют импульсной характеристикой (весовой функцией). Между весовой и переходной функциями звена или системы имеется следующее соотношение:
|
|
|
.
Пример аналитического выражения переходной и весовой функций для колебательного звена:
, 
.
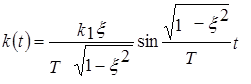При 
колебания становятся незатухающими, а при 
колебания превращаются в апериодический процесс.
Перед выполнением лабораторной работы создать в папке своей группы MathCad-документ, в котором будут оформлены все проводимые работы.
Порядок выполнения работы
1. По таблицам 1 и 2 выбрать исходные данные в соответствии с вариантом задания, состоящим из 2-х цифр.
Таблица 1
| Параметр | Значение | ||||||||||||
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| k1 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 35 | 45 | 55 |
| T1 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,05 | 0,06 | 0,07 | 0,08 | 0,07 | 0,35 | 0,45 |
| T2 | 0,01 | 0,02 | 0,1 | 0,15 | 0,06 | 0,2 | 0,01 | 0,01 | 0,02 | 0,02 | 0,015 | 0,12 | 0,15 |
| 0,4 | 0,5 | 0,6 | 0,5 | 0,3 | 0,4 | 0,7 | 0,8 | 0,5 | 0,3 | 0,25 | 0,25 | 0,25 |
Таблица 2
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Звено | K |  A1
| A2 | K | A1 | A2 | K | A1 | A2 | K | A1 | A2 | K |
где K- колебательное звено;
A1 - апериодическое звено 1-го порядка;
A2 - апериодическое звено 2-го порядка.
2. Сформулировать цель работы и записать исходные данные: дифференциальное уравнение, параметры и передаточную функцию звена.
3. Получить формулы для построения основных характеристик звена.
4. С помощью программы MathCad построить графики основных характеристик.
5. По результатам построения определить время переходного процесса.
6. Исследовать, как изменяется переходная характеристика звена при уменьшении (увеличении) одного из параметров звена.
Контрольные вопросы
1. Что такое передаточная функция звена?
2. Какие основные характеристики звена существуют?
3. Что такое весовая функция?
4. Что такое переходная функция звена?
Переходной функцией 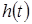называется реакция звена на единичное ступенчатое воздействие, то есть переходный процесс на выходе 
при единичном скачке на входе звена.
5. Как построить АФЧХ звена?
6. Приведите простейшие преобразования, используемые для упрощения структурных схем САУ.
7. Дайте определение обратной связи (положительной и отрицательной).
8. Приведите математические выражения прямого и обратного преобразований Лапласа.
Контрольная работа № 2
Исследование устойчивости систем автоматического регулирования по алгебраическим критериям
Цель работы: исследовать устойчивость системы автоматического регулирования по алгебраическим критериям Рауса и Гурвица.
Теоретическая часть
В теории автоматического регулирования наибольшее применение из алгебраических критериев устойчивости получили критерии Рауса и Гурвица. Эти критерии позволяют по коэффициентам характеристического уравнения замкнутой системы 
без вычисления его корней сделать вывод об устойчивости системы. Общий вид характеристического уравнения следующий:
,
здесь 
i – постоянные коэффициенты, содержащие информацию о САУ.
Критерий устойчивости Рауса
Применение критерия устойчивости Рауса требует составления таблицы. Число строк таблицы равно степени характеристического уравнения плюс единица. В первой строке записывают в порядке возрастания индексов коэффициенты характеристического уравнения, имеющие четный индекс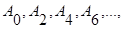 
во второй строке - с нечетным индексом 
...
Любой из остальных коэффициентов таблицы определяется из рекурентного соотношения
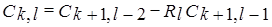, где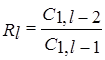 
.
Таблица Рауса
| Номер | Номер столбца | |||
| строки | 1 | 2 | 3 | k 
|
| 1 | 
| 
| 
|  ...
|
| 2 | 
| 
| 
| ... |
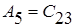
| 3 | 
| 
| 
| ... |
| 4 | 
| 
| 
| ... |
| ... | ... | ... | ... |
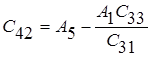
Условие устойчивости: для того чтобы система была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели одинаковый знак. Обычно характеристическое уравнение приводят к такому виду, когда 
>0, для устойчивости системы все остальные элементы первого столбца должны быть положительными.
При наличии отрицательных элементов в первом столбце таблицы Рауса система не устойчива. Число таких элементов равно числу корней характеристического уравнения с положительной вещественной частью.
Если один из элементов первого столбца равен нулю, а остальные элементы положительные, система на границе устойчивости – характеристическое уравнение имеет пару чисто мнимых корней.
При равенстве нулю последнего (n+1)-го элемента или n последних элементов первого столбца система также на границе устойчивости - характеристическое уравнение имеет одну или n пар нулевых корней.
Критерий устойчивости Гурвица
При использовании этого критерия из коэффициентов характеристического уравнения системы составляют таблицу.
По диагонали таблицы от левого верхнего угла выписывают по порядку все коэффициенты, начиная с 
и заканчивая 
. Затем каждый столбец таблицы дополняют так, чтобы вверх от диагонали индексы коэффициентов увеличивались, а вниз — уменьшались. В случае отсутствия в уравнении какого-либо коэффициента и вместо коэффициентов с индексомменьше 0 и больше n пишутнуль.
Критерий можно сформулировать так: система устойчива, если при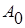 
> 0 положительны и пдиагональных миноров Гурвица, т.е.
; 
; 
; 
; 
.
Это необходимое и достаточное условие устойчивости.
Предпоследнее неравенство есть 
, поэтому последнее неравенство сводится к > 0.
Система находится на границе устойчивости, если 
ивсе предыдущие определители Гурвица положительны. Условие распадается на два: = 0 (апериодическая граница устойчивости, нейтральная устойчивость) или 
(колебательная граница устойчивости).
Раскрывая, например, определители Гурвица для характеристических уравнений третьего, четвертого и пятого порядков, можно получить следующие условия устойчивости:
для системы третьего порядка 
, 
, 
, 
, 
;
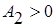для системы четвертого порядка 
, , , , 
, 
;
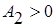для системы пятого порядка 
, , , , , 
;
;
.
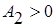Используя критерий Гурвица, можно при заданных параметрах системы принять за неизвестный один какой-либо параметр и определить его предельное значение, при котором система будет находиться на границе устойчивости.
В случае применения критериев Рауса и Гурвица о запасе устойчивости можно судить по тому запасу, с которым выполняются входящие в эти критерии неравенства.
Порядок выполнения работы
1. Для системы, структурная схема которой представлена на рис.3, определить
передаточные функции замкнутой и разомкнутой системы. Здесь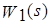 
определяется из 1-ой лабораторной работы, а для передаточных функций остальных звеньев предлагается воспользоваться следующими выражениями:
,
,
.
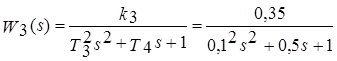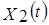
(s) 
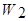(s) 
(s)
(s)
Рис.3. Структурная схема САУ
2. Получить характеристическое уравнение замкнутой системы. Подставить исходные данные и получить числовое выражение характеристического уравнения.
3. Найти корни характеристического уравнения средствами MathCad и по их расположению на комплексной плоскости сделать вывод об устойчивости системы
4. Сформировать таблицу Рауса и сделать вывод об устойчивости системы.
5. Сформировать таблицу Гурвица и сделать вывод об устойчивости системы.
6. Исследовать устойчивость САУ по одному из параметров (по указанию преподавателя) и определить границы устойчивости системы по этому параметру.
Контрольные вопросы
1. В чем заключаются особенности критериев Рауса и Гурвица?
2. Сформулируйте критерий устойчивости системы по Ляпунову.
3. Сформулируйте критерий устойчивости системы по Раусу.
4. Сформулируйте критерий устойчивости системы по Гурвицу.
5. Как можно судить о запасе устойчивости в случае применения критериев Рауса-Гурвица?
Контрольная работа №3
Дата добавления: 2018-10-26; просмотров: 485; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!