Теорема Фурье. Гармонический спектр сложного колебания.

Виды колебаний. - Колебания, возникающие в системе, не подвергающейся внешним воздействиям после называются свободными. - Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса: - При наличии в системе сил трения или сопротивления свободные колебания будут затухающими. - Колебания, возникающие в системе под воздействием переменной внешней силы, называются вынужденными.

Дифференциальное уравнение гармонических колебаний.

Решением дифференциального уравнения такого вида являются уравнения:

или

Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса:

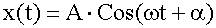
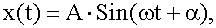
гдеA - амплитуда;

ω - круговая частота;

α - начальная фаза;

( ωt + α ) - фаза.

Фаза колебания

Фаза колебания - это аргумент гармонической функции: ( ωt + α ). Начальная фаза α - это значение фазы в начальный момент времени, т.е. при t = 0.

Амплитуда колебания

Амплитуда колебанияA - это наибольшее значение колеблющейся величины.

Круговая или циклическая частота ω

При изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π .

ω(t + T) +α = ωt + α + 2π,

Время T одного полного колебания называется периодом колебания. Частотойν называют величину, обратную периоду

Единица измерения частоты - герц (Гц), 1 Гц = 1 с-1.

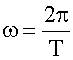
Круговая, или циклическая частоты ω в 2π раз больше частоты колебаний ν. Круговая частота - это скорость изменения фазы со временем.

График гармонического колебания

Дифференциальное уравнение затухающих колебаний.

где β – коэффициент затухания, - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания.

Уравнение затухающих колебаний есть решение такого дифференциального уравнения:

Частота затухающих колебаний:

A = A_oe^–^βt,

где А_о – начальная амплитуда (при t = 0). Видно,что амплитуда уменьшается по экспоненциальному закону.

Подставляя выражение для амплитуды в формулу гармонических колебаний, получим формулу затухающего колебания: А = А_ое^–β^t

Какие процессы называются механическими волнами? Уравнение и график плоской гармонической волны.

Механические волны – процесс распространения механических колебаний в среде (жидкой, твердой, газообразной).

Следует запомнить, что механические волны переносят энергию, форму, но не переносят массу.

Важнейшей характеристикой волны является скорость ее распространения. Волны любой природы не распространяются в пространстве мгновенно, их скорость конечна.

Различают два вида механических волн: поперечные и продольные.

Теорема Фурье. Гармонический спектр сложного колебания.

Французский математик Ж.Б.Фурье доказал, что любое сложное периодическое колебание f(t) можно разложить на сумму простых гармонических колебаний:

F(t) = A_o/2 + Σ A_n.cos(n.ω₁t + φ_n) или

ⁿ

F(t) = A_o/2 + Σ A_n.sin(n.ω₁ + φ_n),

ⁿ

где n = 1,2,3,… (любое целое число). Это положение называется теоремой Фурье.

Каждый член этой суммы принято называть n-й гармоникой {например, слагаемое А₄.cos(4ω₁t +φ₄) - это четвёртая гармоника}. Частота ω₁ (то есть частота первой гармоники) равна частоте самого сложного колебания (соответственно, период первой гармоники равен периоду сложного колебания).

Постоянный член А_о/2 показывает, что колебания происходят не относительно нулевого значения. Например, артериальное кровяное давление в норме колеблется, примерно, от 80 до 120 мм.рт.ст. Это можно представить в виде: АКД = 100 ± 20 мм.рт.ст.; в этом случае А_о/2 = 100. Во многих случаях А_о/2 = 0.

Фурье дал формулы, по которым можно вычислить амплитуды и фазы всех гармоник, если известна формула сложного колебания. К сожалению, эти формулы трудны в применении (требуют вычисления сложных интегралов). В настоящее время эти расчёты проводятся с помощью компьютеров по специальным программам.

В большинстве случаев в сумме участвуют не все гармоники подряд, то есть для каких-то значений n амплитуда А_n= 0. Например, для прямоугольных колебаний с частотой ω (см. рисунок):