Динамічна система більярдної книжки. Інтеграли.

Стр 1 из 2Следующая ⇒

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ “КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ ІМ. І. СІКОРСЬКОГО” Фізико-математичний факультет

Кафедра диференціальних рівнянь

Курсова робота

з дисципліни «Диференціальні рівняння»

«Інтегрувальні "більярдні книжки" моделюють всі 3-атоми інтегровних гамільтонових систем»

Виконав: студент гр. ОМ-61

Жадан І. О.

Затвердив: Пелюх Г. П.

Київ 2018

Зміст

Найпростіша більярдна область.

Більярдна книжка.

Динамічна система більярдної книжки. Інтеграли.

Атом. Молекула.

Загальний вигляд 3-атомів.

6 Моделювання 3-атомів за допомогою більярдних книжок.

Найпростіша більярдна область.

Визначення 1. Сімейством софокусних квадрік називається безліч кривих на площині з Евклідовоми координатами (x, y), що описуються рівнянням

(1)

де a > 0 і b > 0 називаються параметрами цього сімейства, а число λ [0, max (a, b)] - параметром кривої з цього сімейства або параметром квадрики.

Зауваження 1. Без обмеження спільності далі завжди будемо припускати, що b <a.

Зауваження 2. За визначенням вважаємо, що випадок λ = a відповідає прямій x = 0, а випадок λ = b відповідає фокальній прямий y = 0.

Зауваження 3. Крива з сімейства софокусних квадрік є еліпсом при [0, b), гіперболою при (b, a), прямими при λ = a і при λ = b. Еліпси і гіперболи з цього сімейства мають одні і ті ж фокуси і перетинаються під прямим кутом. Пряма в разі = b проходить через них, в разі λ = a є серединним перпендикуляром відрізка, що з'єднує ці фокуси.

Визначення 2. З цим сімейством можна природно зв'язати елліптічеські координати ( , ), де (b, a), (-inf, b)) (див. рис. 1).

Визначення 3. Найпростішою більярдної областю назвемо двовимірне гладке різноманіття ω' з кусочно-гладким краєм, яке може бути вкладено в площину з Евклідовому координатами (x, y) так, що воно буде обмежено і край буде об'єднанням дуг з сімейства софокусних квадрік, кути, спрямовані всередину області, між якими рівні .

Визначення 4. Визначимо Більярдний рух по найпростішої більярдній області, як рух матеріальної частки без тертя по прямим з абсолютно пружним відображенням про кордон області.

Мал. 1: Еліптичні координати.

Мал. 2: Приклад найпростішої більярдної області.

Зауваження 4. Умова на кути у визначенні 3 найпростішої більярдної області є природним. Дійсно, оскільки софокусних квадрики перетинаються під прямим кутом, то кут, спрямований всередину області може дорівнювати тільки і . У разі векторне поле, породжене траєкторіями русі частинки буде не повним. А саме, розглянемо траєкторії, близькі до траєкторії, що потрапляє в кут . У будь-якій її окрестності є траєкторії, які продовжують рух прямо, і траєкторії, які відображаються про кордон області (див. рис. 3). Значить, однозначно виділити продовження траєкторії після проходження кута ми не можемо.

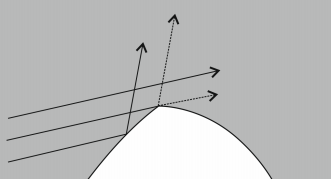
Мал. 3: Приклад, який ілюструє неможливість безперервно визначити траєкторію в разі, коли існує кут на кордоні більярдної області, рівний .

Більярдна книжка.

Визначення 5. Фіксуємо найпростішу більярдну область ω' і число n . Для кожної з дуг границі ω', Що є зв'язковою частиною квадрики припишемо довільну перестановку порядку n з наступними умовами:

1. якщо дві дуги з кордону мають спільну точку, тобто є сусідніми, то перестановки і , приписані їм, коммутируют =

2. до увігнутим з боку більярдної області дуг кордону завжди приписані тотожні перестановки.

Найпростішу більярдну область ω' разом з зазначеними перестановками назвемо склейкою (див. рис. 4).

Визначення 6. Фіксуємо склейку ν. Візьмемо недоладне об'єднання n(ν) найпростіших більярдних областей (листів) ω'(ν), тобто і профактерізуемо за наступним відношенню еквівалентності, залежному від склейки: дуги границь і 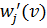будемо вважати еквівалентними, якщо вони відповідають однієї і тієї ж дузі найпростішої більярдної області і їй приписана перестановка , у якій після розкладання її на витвір незалежних циклів i-ий і j-ий елементи знаходяться одному циклі. Вийшов топологічний простір : = - називатимемо більярдної книжкою (або коротко книжкою), що відповідає склеюванню (див. рис. 4).

Зауваження 5. Топологічний простір який вийшов не обов'язково зв'язний.

Визначення 7. Визначимо більярдний рух по книжці, що відповідає склейці, як рух без тертя матеріальної точки (див. рис. 4) по книжці таке, що:

1. всередині всіх листів, з яких складається більярдна книжка, матеріальна точка рухається по прямій без тертя;

2. на кордоні абсолютно пружно відбивається, переходячи на інший аркуш по перестановці , приписаної до дуги, від якої вона відбивається;

3. в точці кута, яка є спільною точкою двох дуг з приписаними перестановками і , вона переходить з листа i на лист ( )(i) та йде в зворотному напрямку.

Зауваження 6. Обмеження на перестановки в визначенні 5 склейки і факторизація у визначенні 6 більярдної книжки є природними.

1. Нехай перестановки і , приписані до сусідніх дуг книжки (першій і другий дузі відповідно), що не комутують. Тобто існує такий лист i, що (i) 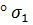(i). Тоді в будь-який околиці траекторії, що йде по листу i в напрямку кута, утвореного цими дугами, є два види траєкторій (див. рис. 5).

Мал. 4: Приклад склейки, відповідної їй більярдної книжки і однієї з траєкторій на ній.

Це траєкторії, котрі вдаряються об першу дугу переходять по перестановці на лист (i), потім вдаряються об другу і переходять на лист (i), продовжуючи на ньому шлях. І траєкторії, які вдаряються спершу про другу дугу переходять по перестановці на лист (i), потім вдаряються об першу і переходять на лист (i), продовжуючи на ньому шлях. Таким чином, в будь-який околиці є неблизькі один до одного траєкторії, які продовжують свій рух на різних аркушах і однозначно визначити траєкторію, що потрапила в кут на i-му аркуші ми не можемо.

2. Нехай до увігнутої дузі книжки приписана нетотожності перестановка . Тоді існує лист i, такий, що (i) i. Оскільки дуга вогнута, то існує траєкторія, яка починає свій рух на i-муаркуші і стосується цієї увігнутою дуги. Тоді в будь-який околиці цієї дуги є траєкторії, які проходять далі по прямій на i-му аркуші, і траєкторії, які вдаряються об увігнуту кордон і переходять на лист (i) (див. рис. 6). Ці траєкторії не близько. Так що знову ми не можемо однозначно визначити траєкторію, що стосується дуги.

Мал. 5: Неможливо однозначно визначити траєкторію в кутку, якщо приписані некоммутуючі перестановки сусіднім дуг.

Мал. 6: Неможливо однозначно визначити траєкторію, торкаючу увігнутою межі, якщо на ній нетотожня перестановка.

Мал. 7: Гранична траєкторія.

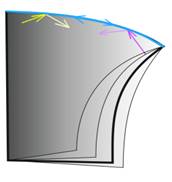3. Деякі невогнуті дуги ми профакторізовалі. Це було необхідно, оскільки для кожної невогнутой дуги існує гранична траєкторія, яка йде тільки по ній. При цьому близькі до цієї траекторії переходять з одного аркуша на інший (див. рис. 7). Тому точки, на цій граничної траєкторії і, відповідно, на цій дузі повинні належати обом листам

Динамічна система більярдної книжки. Інтеграли.

Далі ми будемо вивчати топологічний простір 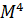- об'єкт динамічної системи більярдної книжки, відповідної склеюванні. визначимо наступним чином:

Визначення 8. Візьмемо недоладне об'єднання n найпростіших білліардних областей , зазначених в склеюванні v і забезпечимо кожну точку вектором швидкості, тобто помножимо на . При цьому існує канонічна проекція , Яка здійснюється забування координат з і того, який зв'язковий компоненті належить точка. Профакторізуємо по відношенню еквівалентності, вказаною нижче, яке описує, як траєкторії відображаються і на який лист переходять (див. рис. 8). Точки ( ) і ( ) з , де , будемо вважати еквівалентними, якщо виконані наступні умови:

2. лежать на границі

3. і мають рівну довжину

4. вектор рівний 0 або ортогонален дотичній до границі області в точці , якщо границя області - гладка в цій точці

5. вектор рівний 0 якщо точка , на границі області є точкою перегину

6. вектор напрямлений із області , вектор всередину області

7. , де – перестановка, приписана до границі області на якій знаходиться точка , якщо границя - гладка в цій точці

8. , де , – перестановки приписані дугам гпвниці області, на якій знаходиться точка , якщо ця точка є точкою перегину на границі області

Отримане після факторизації топологічного простору і будемо позначати далі як .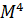

Зауваження 7. Точка на 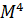- це, по своїй суті, положення матеріальної частини, що рухається по області, яке фіксується точкою на більярдній книжці і її вектором швидкості.

На 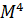є дві функції, які постійні протягом всієї траекторії (інтеграли), - це квадрат модуля вектора швидкості, оскільки ми розглядаємо рух матеріальної частки без тертя і з абсолютно пружним відображенням про границю і параметр квадрік, про який піде мова нижче.

Мал. 8: Приклад, на якому зображена склейка, більярдна книжка, відповідним цієї склеюванні і нижче одним кольором зображені вектори, які ми вважаємо еквівалентними у визначенні 8.

У книзі В.В. Козлова і Д.В. Трещјва [1, гл. 4] сказано, що будь-яка більярдні траєкторія в області, обмеженою дугами софокусних квадрік,торкається деякої іншої софокусних з ними квадрік (див. рис. 9). Це можна перевірити безпосереднім обчисленням в еліптичної системі координат. Дотик в окремому випадку - в еліптичному білліарде випливає з ще більш раннього факту - з класичної теореми Якобі-Шаля [2].

Теорема 1 (Якобі, Шаль). Дотичні прямі до геодезичної лінії на квадрік в n-вимірному евклідовому просторі, проведені у всіх точках геодезичної, стосуються крім цієї квадрік ще n - 1 конфокальної з нею квадрік, одних і тих же для всіх точок геодезичної.

Випадок більярдної книжки в цьому сенсі нічим не відрізняється випадку більярда в області, обмеженою дугами софокусних квадрік. Дійсно, якщо всі листи спроектувати на один, то вийде більярд в найпростішої області , обмежений дугами софокусних квадрік. І тоді, протягом усього траєкторії буде зберігатися параметр квадрік, якої стосується траєкторія після проекції (див. рис. 10). Це і буде ще одним інтегралом.

Мал. 9: На всіх малюнках розглянуто більярд в області, обмеженою дугами софокусних квадрік. На малюнку а) траєкторія стосується софокусних еліпса, на малюнку б) - софокусних гіперболи. Малюнок в) ілюструє більярд в еліпсі. В даному випадку траєкторія стосується ще одного софокусні з ним еліпса.

Явний вигляд інтегралів. Нехай . беремо будь-яку точку 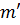з класу еквівалентності точки m. Це буде точка з . І можна співставити їй точку = ( ) в просторі 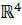, отриману забування, якого з листів належить . Тоді інтеграли матимуть вигляд:

(2)

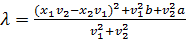(3)

В силу визначення еквівалентності на просторі (Див. Опр. 8) значення функцій не залежить від вибору представника 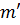, тобто функції коректно заданій.

Визначення 9. Ізоенергетичним топологічним простором назвемо , де v(m) задається рівнянням (2).

Будемо вивчати топологію 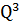, розшаровуючи його на рівні інтеграла 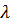. Для цього нам знадобиться інструмент, описаний в книзі [3] А.В. Болсінова, А.Т. Фоменко, а саме: поняття атомів і молекул.

Атом. Молекула.

Розглянемо гладке різноманіття Xn і на ньому гладку функцію f: X R.

Мал. 10: Приклад, який ілюструє, що траєкторія на більярдній книжці також стосується квадрік, софокусних з границею

Визначення 10. Точка x називається критичною для функції f, якщо всі приватні похідні дорівнюють нулю в цій точці. В іншому випадку точка називається регулярною.

Визначення 11. Критична точка x називається невироджених для функції f, якщо визначник матриці приватних похідних відмінний від нуля.

Визначення 12. Рівень (f = c) називається критичним, якщо на цьому рівні є хоча б одна критична точка, в іншому випадку він називається регулярним.

Визначення 13. Гладка функція називається функцією Морса, якщо всі її критичні точки невирождені.

Нехай f - функція Морса.

Визначення 14. Введемо на X наступне відношення еквівалентності: на кожному рівні функції f точки 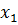і X будемо вважати еквівалентними, якщо вони належать одній компоненті зв'язності. Профакторизуемо X по відношенню еквівалентності і отримаємо якийсь граф (див. рис. 11), який називається графом Риба для функції f на топологічному просторі X.

Мал. 11: Граф Риба для функцій висоти на торі і сфері з двома ручками

Мал. 12: Молекула для функцій висоти на торі і сфері з двома ручками

Визначення 15.Розглянемо досить малу - окол деякої точки графа Риба, що належить зв'язковий компоненті шару, де є критична точка. Її прообраз з точністю до пошарового гомеоморфізму будемо називати атомом.

Зауваження 8. Всі вершини графа Ріба лежать на критичному шарі. Крім того, безліч критичних значень має міру нуль, а в прообраз всіх Регулярні значень лежить n – 1 мірний тор.

Визначення 16. Граф Риба разом із зазначеними атомами у відповідних точках на ньому сидів, зветься грубою молекулою для функції f на різноманітті X (див. рис. 12).

Введені вище визначення спочатку були визначені для гладких функцій Морса на різноманітті. Але, оскільки в нашому випадку це не так, ми узагальнимо цю конструкцію до випадку, коли X топологічний просторі, у якого майже всі точки діффеоморфни диску , А функція f: X R на ньому тільки безперервна.

Граф Ріба можна визначити таким же способом.

Визначення 17. Розглянемо прообраз точки на графі, яка не гомеоморфний n - 1-мірного тору. Прообраз досить малій - околі цієї точки з точністю до пошарового гомеоморфізму назвемо атомом.

Визначення 18. Граф Риба з зазначеними атомами в відповідних точках назвемо грубою молекулою для функції f на топологічному просторі X.

Зауваження 9. Ясно, що в разі, коли X - гладке двовимірне або трьохмірне різноманіття, а f - гладка функція Морса, таке визначення буде збігатися з більш раннім. Тому, це дійсно узагальнення визначень.

У разі, коли X - гладке двовимірне або тривимірне різноманіття, а f - гладка функція Морса, в книзі [3] А.В. Болсінова, А.Т. Фоменко в явному вигляді описаний вид всіх атомів і молекул. Крім того, якби 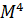у нас було гладким різноманіттям, то теорема Ліувілля дала б нам те, що в прообраз всіх регулярних значень знаходяться тори. У нашому випадку ми не можемо користуватися обома цими фактами, так що будемо доводити вид молекули незалежно. Однак, аналогія з гамільтоновим динамічними системами існує. В теорії гамільтонових динамічних систем молекула описує топологію околиці кожного окремого рівня. Тому, описавши молекулу нашої динамічної системи, ми зможемо вказати з якими динамічними системами і в який околиці збігається наша.

Загальний вигляд 3-атомів.

У разі, коли різноманіття X має розмірність 2, то атоми будемо називати 2-атомами, коли розмірність 3 - 3-атомами.

Нижче в розділі буде описана теорія, детально викладена в книзі [3] А.В. Болсінова, А.Т. Фоменко.

2-атоми описують перебудову одного кількості кіл в інше, 3-атоми - перебудову торів, так як на ребрах стоять регулярні точки. Атоми бувають двох сортів: атоми типу A (мінімуму і максимуму функції) і сідлові атоми. Атоми першого типу пошарово гомеоморфні двовимірному диску D, розшарування на окружності, в разі 2-атома і , розшароване на тори, в разі 3-атома.

Визначення 19. Крестом називається прообраз - околі точки 0 функції , заданої в деякій околиці точки (0, 0) зі структурою шарування, необхідної для того, щоб говорити про пошаровому гомеоморфізмом (Див. Рис. 13). Тут рівень 0 - критичний.

Будь-який сідловий 2-атом P може бути склеєний з k N хрестів так, щоб кожен рівень , на одному хресті склеювався відповідним рівнем на іншому хресті (див. Рис. 14). k називається складністю атома P.

Мал. 13: Хрест. Зафарбовані рівні c ( , 0), що не зафарбовані рівні c (0, + ).

Мал. 14: Таблиця некторих 2-атомів. Тут можна явно побачити, як потрібно склеювати хрести, щоб отримати атом.

Можуть вийти, як орієнтуються (як самостійне різноманіття) атоми, так і неоріентіруемі. Ориентовні атоми можуть бути занурені в площину. Природно пов'язувати з 2-атомом граф, який є прообразом критичних рівнів, кілька кілець, які є прообразом ( 0) і кілька кілець, які є прообразом (0, ). У такого графа вершини можуть бути тільки кратності 0 або 4.

Зауваження 10. 3-атоми бувають також, як орієнтуються, так і неорієнтовні. Якщо на якомусь рівні виникає неорієнтовний атом, то різноманіття в цілому виходить неорієнтовним. В теорії інтегруються гамільтонових систем бувають тільки орієнтуються різноманіття, тому питання про подання неоріентіруемих 3-атомів поки неактуальний.

Будь орієнтується седловой 3-атом може бути отриманий одним з двох способів:

1. Прямим твором деякого орієнтованого седлового 2-атома

на окружність .

2. Другий спосіб влаштований трохи складніше. Тут ми отримаємо атом з зірочками. Нехай дано 2-мірний орієнтується седловой атом . для визначеності фіксуємо на н м функцію , яка задає шарування. Припустимо, що на ньому задана інволюція, тобто гладке відображення , що володіє наступними властивостями:

(а) = id,

(б) зберігає рівень, тобто ( (x)) = (x),

(в) зберігає орієнтацію,

(г) деякий кінцеве число критичних точок є нерухомими точками інволюції .

Для побудови 3-атома розглянемо циліндр P [0, 2] і склеим його підстави по інволюції , ототожнюючи точки (x, 2 ) і ( (x), 0). В редок ми отримаємо Ориентовні 3-різноманіття U c краєм. функція f природним чином продовжується на U, оскільки ( (x)) = (x), і її поверхні рівня задають структуру шарування на U з єдиним особливим шаром. Відзначимо, що топологічно різноманіття U є розшаруванням над окружністю з шаром . Якщо профакторізовати по інволюції , отримаємо інший 2-атом P. Виділимо на ньому зірочками точки на критичній окружності, які зберігаються під дією інволюції . Отриманий 2-атом P з виділеними зірочками називається атомом із зірочками, а 2-атом називається дублем P.

Іноді в після факторизації виходить кільце, розшарування на окружності. У цьому випадку будемо вважати, що у нас атом A із зірочками. Ясно, що дубль P є розгалуженим дволистої накриттям над 2-атомом P, причому точками розгалуження є якраз зірочки атома P.

Слід мати на увазі, що дублів у одного атома із зірочкою може бути кілька і всі вони ставлять одне і те ж 3-атом. Тому різноманіття U однозначно визначається атомом із зірочками P. Зв'яжемо з таким атомом граф, який є графом для 2-атома P, але додамо до безлічі його вершин зірочки. Складність атома зі зірочкою - це число вершин його графа.

Таким чином всі орієнтвні 3-атоми можна описати орієнтовній 2-атомами і орієнтується 2-атомами, на яких стоїть кінцеве число зірочок на критичному рівні.

Приклад 1. На рис. 17 наведено приклад простого 3-атома A*. Він влаштований дещо складніше атома В (див. рис. 16), який є прямим виділенням восьми РСІ на коло. Потрібно видалити з полноторія лише одне тонке полноторіе, але які обходяться два рази вздовж осі. Особливий шар L виходить протягуванням уздовж окружності обертається вісімки, встигає провернутися на кут за один оборот. При проходженні через особливий рівень один тор перебудовується в один тор.

Мал. 15: 3-атом A.

Рис. 16: 3-атом B.

Рис. 17: 3-атом A.

Дата добавления: 2018-06-27; просмотров: 367; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!