Получение статистических данных
Министерство образования и науки Российской Федерации
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ (НИ ТГУ)
Геолого-географический факультет
Кафедра минералогии и геохимии
Контрольная работа по курсу
«Математические методы моделирования в геологии»
Вариант № 12
Преподаватель
Е.М. Асочакова
__________ подпись
«_____»__________2018 г.
Студентка ОЗО группа 02380
А.К. Шакирова
___________ подпись
Томск, 2018
Содержание
Введение. 3
1. Статистические характеристики, используемые в геологии. 6-10
2. Закон распределения данных. 11-13
3. Дисперсионный анализ. 14-18
4. Корреляционный анализ. 19-21
5. Регрессионный анализ. 22-25
6. Нелинейная регрессия. 26-27
7. Кластерный анализ. 28-31
8. Факторный анализ. 34-36
Заключение. 37
Введение
На современном этапе развития естественных наук, под влиянием научно-технического прогресса происходят существенные изменения методов научных экспериментов, анализа и обобщения получаемых результатов. Этому способствуют не только расширившиеся возможности фундаментальных наук, но также бурное развитие электронно-вычислительной техники и комплексной автоматизации самых разнообразных видов человеческой деятельности. В последние десятилетия наблюдается глубокое проникновение математических методов исследования во все отрасли естественных наук, что способствовало исключительным успехам некоторых из них, например биологии, метеорологии и др. Для успешного развития геологических наук необходимо также использовать полный арсенал существующих прогрессивных научных и технических средств, включая математические методы.
|
|
|
Основная цель данной работы выяснить и понять распределение полезных компонентов в пределах Восточного Забайкалья, по данным полученным в результате опробования керна скважин и проведения рентгенофлуоресцентного анализа проб.
Для достижения поставленной цели будут решаться следующие задачи:
1. научиться применять математические методы для обработки геологической информации;
2. научиться формулировать геологические задачи в пригодном виде для их решения математическими методами;
3. научится применять наиболее эффективные методы;
4. понять основные принципы геолого-математического моделирования;
5. установить возможность применения геолого-математического моделирования для данного участка.
Таблица №1 Исходные данные для достижения поставленной цели
| №пп | Порода | № образца | SiO2 | TiO2 | Al2O3 | Fe2O3 | MnO | MgO | CaO | Na2O | K2O | P2O5 | ППП
| Сумма | ||
| 1 | Метаандезит | HC 167/6 | 42,1 | 3,8 | 14,2 | 23,0 | 0,1 | 3,9 | 0,9 | 3,1 | 0,7 | 0,9 | 6,8 | 99,4 | ||
| 2 | Метаандезит | HC 177/30 | 55,0 | 0,7 | 14,2 | 6,1 | 0,1 | 4,7 | 4,9 | 1,9 | 2,1 | 0,1 | 8,5 | 98,4 | ||
| 3 | Метаандезит | HC 177/24 | 51,5 | 0,7 | 14,1 | 5,9 | 0,1 | 5,5 | 6,9 | 0,6 | 3,4 | 0,1 | 12,1 | 100,9 | ||
| 4 | Метаандезит | 177-153 | 66,1 | 0,4 | 12,6 | 4,0 | 0,1 | 1,6 | 4,7 | 3,7 | 2,2 | 0,0 | 4,3 | 99,6 | ||
| 5 | Метаандезит | HC 166/13-2 | 67,3 | 0,5 | 10,2 | 5,2 | 0,1 | 4,5 | 4,4 | 0,4 | 1,3 | 0,1 | 6,2 | 100,1 | ||
| 6 | Метаандезит | HC 177/25 | 46,8 | 0,7 | 17,6 | 5,6 | 0,1 | 5,8 | 6,0 | 1,0 | 7,2 | 0,0 | 8,5 | 99,3 | ||
| 7 | Метаандезит | HC 166/15-1 | 46,0 | 0,9 | 16,3 | 5,1 | 0,2 | 3,2 | 12,9 | 0,4 | 3,7 | 0,2 | 11,7 | 100,7 | ||
| 8 | Метаандезит | HC 166/5 | 44,4 | 0,6 | 12,9 | 5,8 | 0,2 | 3,1 | 15,3 | 0,6 | 2,2 | 0,1 | 15,2 | 100,4 | ||
| 9 | Метаандезит | NK-4/5 | 52,2 | 0,7 | 15,4 | 7,8 | 0,1 | 8,2 | 6,8 | 0,1 | 1,8 | 0,1 | 5,3 | 98,4 | ||
| 10 | Метаандезит | K-59-159 | 40,2 | 0,5 | 6,9 | 7,3 | 0,1 | 4,2 | 21,7 | 1,9 | 0,8 | 0,1 | 15,4 | 99,0 | ||
| 11 | Метаандезит | HC 170/11 | 59,5 | 0,9 | 19,9 | 5,6 | 0,1 | 2,7 | 1,5 | 0,7 | 2,9 | 0,2 | 6,2 | 100,1 | ||
| 12 | Дацит | NK-4/7 | 42,9 | 0,7 | 9,5 | 5,8 | 0,1 | 4,8 | 15,3 | 2,6 | 1,9 | 0,3 | 14,8 | 98,7 | ||
| 13 | Дацит | K-69/11 | 56,5 | 1,1 | 14,4 | 8,0 | 0,1 | 4,3 | 7,8 | 2,4 | 1,6 | 0,4 | 2,3 | 98,9 | ||
| 14 | Дацит | NK-5/3 | 63,5 | 0,9 | 15,2 | 4,4 | 0,1 | 2,0 | 5,1 | 0,1 | 3,5 | 0,2 | 4,9 | 99,9 | ||
| 15 | Дацит | NK-5/4 | 57,4 | 0,8 | 14,9 | 6,3 | 0,1 | 3,7 | 5,2 | 1,0 | 2,6
| 0,2 | 7,2 | 99,5 | ||
| 16 | Дацит | NK-3/2 | 59,5 | 0,6 | 21,3 | 3,7 | 0,1 | 1,5 | 3,7 | 2,3 | 3,2 | 0,1 | 3,1 | 98,9 | ||
| 17 | Дацит | NK-4/4 | 58,1 | 1,0 | 16,6 | 5,7 | 0,1 | 3,7 | 5,4 | 2,9 | 2,0 | 0,3 | 4,5 | 100,2 | ||
| 18 | Дацит | NK-4/7 | 50,8 | 1,0 | 16,2 | 5,7 | 0,1 | 3,7 | 9,2 | 3,8 | 2,4 | 0,4 | 5,4 | 98,7 | ||
| 19 | Дацит | NK-3/1 | 64,2 | 1,2 | 17,6 | 6,4 | 0,1 | 1,2 | 1,9 | 0,8 | 2,3 | 0,3 | 3,9 | 99,8 | ||
| 20 | Дацит | k-54-35.0 | 44,1 | 3,3 | 17,3 | 16,3 | 0,2 | 3,4 | 1,8 | 0,7 | 0,8 | 0,7 | 10,8 | 99,4 | ||
| 21 | Дацит | k-59-130 | 46,4 | 0,8 | 14,3 | 6,4 | 0,1 | 4,6 | 11,6 | 1,3 | 2,2 | 0,5 | 10,9 | 99,3 | ||
| 22 | Метадацит | k-52-21.5 | 45,0 | 2,9 | 11,4 | 13,2 | 0,2 | 3,1 | 10,5 | 2,3 | 0,6 | 0,4 | 10,4 | 100,0 | ||
| 23 | Метадацит | k-51-32 | 47,0 | 1,5 | 9,1 | 12,7 | 0,2 | 4,6 | 9,4 | 3,0 | 0,4 | 0,2 | 11,2 | 99,2 | ||
| 24 | Метадацит | k-53-12.0 | 76,0 | 0,2 | 13,9 | 2,9 | <0.05 | 0,8 | 0,4 | 2,5 | 1,4 | 0,1 | 2,1 | 100,4 | ||
| 25 | Метадацит | 155-11.9 | 46,1 | 1,5 | 13,2 | 9,4 | 0,3 | 1,4 | 12,4 | 0,5 | 2,2 | 0,1 | 13,1 | 100,1 | ||
| 26 | Метадацит | k-52-4.1 | 49,8 | 3,1 | 10,3 | 16,8 | 0,2 | 2,5 | 5,3 | 3,5 | 0,7 | 0,6 | 7,1 | 99,8 | ||
| 27 | Андезит | 201-50 | 59,2 | 0,3 | 18,6 | 1,8 | 0,1 | 3,9 | 3,6 | 0,5 | 2,8 | 0,1 | 8,4 | 99,3 | ||
| 28 | Андезит | 204-34 | 44,0 | 1,9 | 13,3 | 14,1 | 0,2 | 6,2 | 5,0 | 1,3 | 1,2 | 0,6 | 7,8 | 95,6 | ||
| 29 | Метадацит | 207-99 | 64,7 | 0,3 | 16,4 | 2,0 | 0,1 | 2,9 | 2,6 | 2,1 | 2,8 | 0,2 | 5,3 | 99,3 | ||
| 30 | Метадацит | A-1 | 72,7 | 0,3 | 15,7 | 2,6 | 0,0 | 0,4 | 0,1 | 4,6 | 1,6 | 0,1 | 1,4 | 99,5 | ||
| 31 | Метадацит
| A-3 | 69,2 | 0,3 | 17,4 | 1,4 | 0,0 | 1,0 | 1,7 | 2,6 | 3,1 | 0,2 | 2,3 | 99,2 | ||
| 32 | Метадацит | A-6 | 65,7 | 0,6 | 14,8 | 5,0 | 0,1 | 3,9 | 2,8 | 2,4 | 1,4 | 0,1 | 2,2 | 99,0 | ||
| 33 | Андезит | 205-94 | 56,3 | 0,5 | 15,5 | 3,6 | 0,1 | 6,1 | 4,9 | 2,0 | 2,0 | 0,1 | 8,2 | 99,3 | ||
| 34 | Андезидацит | 205-101 | 54,2 | 0,6 | 15,1 | 3,8 | 0,1 | 8,8 | 4,7 | 1,2 | 2,7 | 0,2 | 8,1 | 99,5 |
Статистические характеристики, используемые в геологии
Минимальное значение – наименьшее возможное значение.
Максимальное значение – наибольшее возможное значение.
Среднее значение - статистический обобщенный показатель какой либо величины.
Среднее арифметическое - (в математике и статистике) множества чисел — число, равное сумме всех чисел множества, делённая на их количество.

Среднее арифметическое взвешенное - общее название группы разновидностей среднего значения либо короткое название для любого из перечисленных: Среднее арифметическое взвешенное Среднее геометрическое взвешенное Среднее гармоническое взвешенное.
Среднее арифметическое взвешенное набора чисел x1……xn с весами ω1……ωn определяется как:
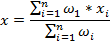
Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось.

Среднее степенное – любое число отличительное от нуля.
Среднее степени d (или просто среднее степенное) набора положительных вещественных чисел x1,…,xn определяется как:

Среднее квадратическое – число S, равное квадратному корню среднего арифметического квадратов данных чисел a1,a2,…,an:

Среднее гармоническое – один из способов, которым можно понимать «среднюю» величину некоторого набора чисел. Его можно определить следующим образом: пусть даны положительные числа x1,…xn, тогда их средним гармоническим будет такое число H, что

Можно получить явную формулу для среднего гармонического:

т.е. срежнее гармоническое есть обратная величина к среднему от обратных к числам x1,…,xn.
Медиана – середина, в математической статистике – число, характеризующее выборку (например набор чисел). Если все элементы выборки различны, то медиана — это такое число выборки, что ровно половина из элементов выборки больше него, а другая половина меньше него. В более общем случае медиану можно найти, упорядочив элементы выборки по возрастанию или убыванию и взяв средний элемент. Например, выборка {11, 9, 3, 5, 5} после упорядочивания превращается в {3, 5, 5, 9, 11} и её медианой является число 5. Если в выборке чётное число элементов, медиана может быть не определена однозначно: для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора {1, 3, 5, 7} принимают равной 4).
Мо́да - значение во множестве наблюдений, которое встречается наиболее часто. (Мода = типичность.) Иногда в совокупности встречается более чем одна мода (например: 6, 2, 6, 6, 8, 9, 9, 9, 0; мода — 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило, мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.
Квартили - предоставляют важную информацию о структуре вариационного ряда к-л признака. Вместе с медианой они делят вариационный ряд на 4 равные части. Квартилей две, их обозначают символами Q, верхняя и нижняя квартиль. 25% значений меньше, чем нижняя квартиль, 75% значений меньше, чем верхняя квартиль.
Для расчёта квартили надо поделить вариационный ряд медианой на две равные части, а затем в каждой из них найти медиану. К примеру, если выборка состоит из 6 элементов, тогда за начальную квартиль выборки принимается второй элемент, а за нижнюю квартиль пятый элемент.

Рисунок 1. Квартили
В случае, если вариационный ряд состоит к примеру, из 9 элементов, тогда за верхнюю квартиль принимают арифм. среднее 2-го и 3-го элеметов, а за нижнюю арифм. среднее 7-го и 8-го элементов.
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9.
Квантили – значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Если вероятность задана в процентах, то квантиль называется перцентилем. Например, для развитых стран 95-процентиль продолжительности жизни составляет 100 лет, означает, что ожидается, что 95% людей не доживут до 100 лет.
Дисперсия – мера разброса значений случайной величины относительно ее математического ожидания. Обозначается D[X] в русской литературе и Var(X) в зарубежной. В статистике часто употребляется значение σ2x или σ2.
Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние, среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок (измерений), это среднее арифметическое называют оценкой математического ожидания.
Коэффициент вариации - Мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет её средний разброс.
Коэффициент вариации равен отношению стандартного отклонения к среднему значению:

Коэффициент вариации имеет смысл использовать при ненулевых средних значениях.
Коэффициент полезен в ситуациях, когда о размерах отклонения величины можно судить, зная ее среднее значение.
Иногда предлагается условная классификация вариабельности выборки на основе коэффициента вариации: при выборка вариабельна слабо, при - средне, при - сильно.
Асимметрия представляет собой числовое отображение степени отклонения графика распределения показателей от симметричного графика распределения. Если асимметрия больше 0, то чаще в распределении встречаются значения меньше среднего. Такая асимметрия называется положительной или левосторонней.
Коэффициент эксцесса - (коэффициент островершинности) в теории вероятностей — мера остроты пика распределения случайной величины.
Пусть задана случайная величина X, такая что E│X│4<∞. Пусть µ4 обозначает четвертый центральный момент: µ4 = E [(X – EX)4], а  – стандартное отклонение X. Тогда коэффициент эксцесса задается формулой:
– стандартное отклонение X. Тогда коэффициент эксцесса задается формулой:

Получение статистических данных
Для получения статистических данных была применена компьютеризированная программа Statistika. С помощью этой программы достаточно быстро удалось обработать полученные данные рентгенофлуорисцентного анализа из керна скважины пробуренной в пределах Черемховского участка.
С помощью программы Statistica удалось получить такие статистические данные как:
среднее значение; среднее гармоническое; среднее геометрическое;медиана; мода; частота моды; сумма; минимум; максимум; нижняя квартиль; верхняя квартиль; размах; квартиль размаха; дисперсия; стандартное отклонение; асимметрия; эксцесс.
Полученные статистические данные указаны в таблице №2.
Таблица №2
Статистические данные
|
| № набл | Среднее | Геометр среднее | Гармон среднее | Медиана | Мода | Част. моды | Сумма | Мин | Макс | Ниж кварт | Верх кварт | Дисперсия | Стд. Откл | Ассиметрия | Эксцесс |
| SiO2 | 34 | 54,83 | 54,02475 | 53,2383 | 54,6 | 59,500 | 2 | 1864,4 | 40,20 | 76,0 | 46,1 | 63,500 | 93,5 | 9,6723 | 0,3867 | -0,8416 |
| TiO2 | 34 | 1,052 | 0,80076 | 0,63776 | 0,70 | 70000 | 5 | 35,800 | 0,200 | 3,80 | 0,50 | 1,1000 | 0,82 | 0,9099 | 1,8800 | 2,7917 |
| Al2O3 | 34 | 14,59 | 14,24150 | 13,8332 | 14,8 | Множ. | 2 | 496,30 | 6,900 | 21,3 | 13,2 | 16,400 | 9,50 | 3,0825 | -0,3667 | 0,4657 |
| Fe2O3 | 34 | 7,041 | 5,80115 | 4,77528 | 5,75 | Множ. | 2 | 239,40 | 1,400 | 23,0 | 4,00 | 7,8000 | 23,0 | 4,7976 | 1,6792 | 2,8771 |
| MnO | 34 | 0,119 |
|
| 0,10 | 10000 | 23 | 4,050 | 0,000 | 0,30 | 0,10 | 0,1000 | 0,00 | 0,0603 | 0,8436 | 1,6451 |
| MgO | 34 | 3,702 | 3,10480 | 2,34481 | 3,70 | Множ. | 3 | 125,90 | 0,400 | 8,80 | 2,50 | 4,6000 | 3,80 | 1,9503 | 0,5877 | 0,6159 |
| CaO | 34 | 6,364 | 4,34886 | 1,65215 | 5,05 | Множ. | 2 | 216,40 | 0,100 | 21,7 | 2,80 | 9,2000 | 23,9 | 4,8974 | 1,2631 | 1,6662 |
| Na2O | 34 | 1,788 | 1,28798 | 0,71203 | 1,90 | Множ. | 2 | 60,800 | 0,100 | 4,60 | 0,70 | 2,6000 | 1,43 | 1,1976 | 0,4202 | -0,6968 |
| K2O | 34 | 2,167 | 1,84461 | 1,51307 | 2,15 | 2,2000 | 4 | 73,700 | 0,400 | 7,20 | 1,40 | 2,8000 | 1,58 | 1,2576 | 1,8551 | 6,7240 |
| P2O5 | 34 | 0,244 |
|
| 0,20 | 10000 | 13 | 8,300 | 0,000 | 0,90 | 0,10 | 0,3000 | 0,04 | 0,2091 | 1,5022 | 2,0078 |
| ППП | 34 | 7,517 | 6,37091 | 5,14775 | 7,15 | Множ. | 2 | 255,60 | 1,400 | 15,4 | 4,50 | 10,800 | 15,7 | 3,9638 | 0,3890 | -0,6746 |
Закон распределения данных
Законом распределением случайной величины называют соответствие между возможными значениями и их вероятностями.
Точечное оценивание - это вид статистического оценивания, при котором значение неизвестного параметра q приближается отдельным числом.
Суть точечного оценивания в том, что для τ(q) строится одна статистика t(x) = τ, которая принимается за оценку τ(q), т.е. t(x) = τ. «Хорошей» оценкой является такая оценка, которая наиболее близка к истинному значению τ(q), т.е. когда ее значения в каком-то смысле сконцентрированы вокруг истинного значения τ(q) [1].
Задача точечного оценивания
Исследуется случайная величина X, распределение которой относится к параметрическому множеству Fq(x), где q (q1,..., qk) – неизвестный k-мерный параметр.
Имеется выборка наблюденных значений случайной величины Fq(x):t = t(q) oбъема выборки n. Требуется построить точечную оценку (статистику) для данной функции t = t(q) и исследовать качество данной оценки.
Cвойства точечных оценок t=t(x)
a) Несмещенность: Et(x) = t(q) (EX – математическое ожидание случайной величины Fn(x)) или асимптотическая несмещенность Et(x) ¾¾¾®t(q), при n®¥ [2].
б) Состоятельность:Одно из самых очевидных требований к точечной оценке заключается в том, чтобы можно было ожидать достаточно хорошего приближения к истинному значению параметра при достаточно больших значениях объема выборки n. Это означает, что оценка t(x) должна сходиться к истинному значению t(q) при n®¥. Это свойство оценки и называется состоятельностью. Поскольку речь идет о случайных величинах, для которых имеются разные виды сходимости, то и данное свойство может быть точно сформулировано по-разному:
- если t(x) сходится к истинному значению t(q) с вероятностью 1 (почти наверное), то тогда оценка называется сильно состоятельной;
- если имеет место сходимость по вероятности, то тогда оценка называется слабо состоятельной.
Условие состоятельности является практически обязательным для всех используемых на практике оценок. Несостоятельные оценки используются крайне редко [1].
в) Эффективность несмещенной оценки характеризуется дисперсией Dt(x) и используется для сравнения качества несмещенных оценок.
Одновременное выполнение этих желательных свойств не всегда возможно, поэтому представление о «хорошей» оценке зависит от цели и возможностей исследования, определяющих приоритетные свойства оценки. Так, для малых выборок часто важна несмещенность оценки, а для больших – асимптотическая несмещенность и состоятельность. А иногда, сознательно отказываясь от одних свойств оценок, добиваются выполнения других, более важных с точки зрения исследования свойств [2].
Интервальная оценка среднего
Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра.
Предположим, что x= x1,...,xn – выборка объёма n наблюдений над случайной величиной Х, распределение которой относится к параметрическому семейству Fθ(х), где θ = (θ1,…, θк) и θ Î Θ (Θ − параметрическое множество). Требуется оценить некоторую функцию τ = τ(θ). Доверительное оценивание τ означает нахождение k-мерной области, заключающей неизвестное значение функции τ с заданной доверительной вероятностью γ. Искомое доверительное множество становится доверительным интервалом, и задача состоит в построении двух статистик t1 = t1(x) и t2 = t2 (x) (концов доверительного интервала J = (t1,t2), заключающего в себе неизвестное значение параметра θ с заданной доверительной вероятностью γ: γ = P (t1<θ<t2).
При доверительном оценивании заданное значение γ (обычно близкое к единице) означает надёжность оценивания τ(θ) с точностью, определяемой размером доверительной области. При построении доверительного интервала для параметра θ его длина – точность оценивания, а γ – заданная надежность. Поэтому желательно строить кратчайший доверительный интервал, соответствующий наибольшей точности при данном γ.
Общий приём при нахождении доверительного интервала состоит в построении центральной статистики Z = Z(θ), т.е. такой статистики, распределение которой не зависит от неизвестного параметра θ. Если Z(θ) непрерывна и монотонна по θ, то это обеспечивает однозначную эквивалентность событий {t1* < Z < t2*} и {t1 < θ <t2*}. Тогда, если удалось найти t1* = t1*(θ) и t2* = t2*(θ) − нижнюю и верхнюю доверительные границы, то решая неравенство t1* < Z < t2* относительно θ, находим значения t1 и t2 − искомые границы доверительного интервала для неизвестного параметра θ [2].
Дисперсионный анализ
Дисперсионный анализ — метод в математической статистике, направленный на поиск зависимостей в экспериментальных данных путём исследования значимости различий в средних значениях. В отличие от t-критерия, позволяет сравнивать средние значения трёх и более групп. Разработан Р. Фишером для анализа результатов экспериментальных исследований.
Суть дисперсионного анализа сводится к изучению влияния одной или нескольких независимых переменных, обычно именуемых факторами, на зависимую переменную. Зависимые переменные представлены значениями абсолютных шкал (шкала отношений). Независимые переменные являются номинативными (шкала наименований), то есть отражают групповую принадлежность, и могут иметь две или более градации (или уровня). Примерами независимой переменной Xi с двумя градациями могут служить пол (женский: X1, мужской: X2) или тип экспериментальной группы (контрольная X1, экспериментальная: X2). Градации, соответствующие независимым выборкам объектов, называются межгрупповыми, а градации, соответствующие зависимым выборкам, — внутригрупповыми.
В зависимости от типа и количества переменных различают:
однофакторный и многофакторный дисперсионный анализ (одна или несколько независимых переменных);
одномерный и многомерный дисперсионный анализ (одна или несколько зависимых переменных);
дисперсионный анализ с повторными измерениями (для зависимых выборок);
дисперсионный анализ с постоянными факторами, случайными факторами, и смешанные модели с факторами обоих типов;
Дата добавления: 2018-06-27; просмотров: 330; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
