Векторды базистер бойынша жіктеу
Дәріс №1 Векторлар және векторларға қолданылатын сызықтық амалдар Вектор ұғымы. Физика, механика және техника салаларында скалярлық және векторлық шамалар жиi кездеседi. Өзiнiң сандық мәнiмен толық анықталатын шамаларды скалярлық шамалар деп атайды. Скалярлық шамаларға мысалдар: аудан, ұзындық, көлем, масса, жұмыс, температура. Векторлық шамалар өздерiнiң сандық мәндерiмен және бағыттарымен анықталады. Векторлық шамаларға мысалдар: күш, жылдамдық, үдеу. Вектор деп бас нүктесi -да соңғы нүктесi -да жататын бағытталған кесiндiсiн айтады. векторы (бас нүктесi -да, ал соңғы нүктесi -да) векторға қарама-қарсы вектор деп аталады. векторына қарама-қарсы вектор деп белгiленедi. вектордың ұзындығы немесе модулi деп кесiндiнiң ұзындығын айтады да оны деп белгiлейдi. Ұзындығы нөлге тең векторды нөлдiк вектор деп атайды да деп белгiлейдi. Нөлдiк вектордың бағыты жоқ. Ұзындығы бiрге тең векторды бiрлiк вектор немесе орто деп атайды. вектордың бiрлiк векторының бағыты осы вектормен бағыттас, оны деп белгiлейдi. және векторларын коллинеарлы дейдi, егер олар бiр түзудiң бойында немесе параллель түзулерде жатса, онда оларды деп жазады. Екi және векторларын бiр-бiрiне тең дейдi , егер олардың ұзындықтары тең болса және бағыттары бiрдей болса. Осы анықтамадан келешекте өзiне өзiн параллель жылжыта алатын векторлар қарастырылады. Вектордың бас нүктесiн кеңiстiктiң кез келген нүктесiне параллель жылжытып алып келуге болады. Кеңiстiктегi үш векторларды компланарлы дейдi, егер олар бiр жазықтықта немесе параллель жазықтықтарда жатса. Векторларға қолданылатын сызықтық амалдар. Векторларды қосу, азайту және векторларды санға көбейтудi векторларға қолданылатын сызықтық амалдар дейдi. Кеңiстiкте және кез келген екi вектор берiлсiн. Кез келген нүктесiн алып векторын тұрғызамыз. нүктесiнен векторын тұрғызамыз. және векторлардың қосындысы деп вектордың басы мен вектордың соңғы нүктесiн қосатын векторын айтады. келесi суретте үш және векторлардың қосындысы келтiрiлген. Екi және векторлардың айырымы деп және векторлардың қосындысы болатын векторын айтады. с=а-b Атап өтетiн жағдай, және векторларынан тұрғызылған параллелограммның бiр диагоналы, және векторлардың қосындысы, ал екiншiсi айырымы болады. вектордың нақты санға көбейтiндiсi деп ұзындығы тең, векторына коллинеарлы, егер болса, онда векторына бағыттас, егер онда векторына қарама-қарсы бағыттас векторын айтады. Векторларға қолданылатын сызықтық амалдардың қасиеттері: 1) Векторларды қосу коммутативті , 2) Векторларды қосу ассоциативті , 3) , 4) , 5) Векторларды санға көбейту ассоциативтi , , 6) , 7) Векторды санға көбейту сандарды қосуға қарағанда дистрибутивті , , 8) Векторларды санға көбейту векторларды қосуға қарағанда дистрибутивті , Осы сегіз қасиетті қанағаттандыратын векторлар жиын кеңістігі, сызықты немесе векторлық кеңістік деп аталады. Бұл кеңістікті деп белгілейді. Дәріс №2. Вектордың проекциясы. Векторлардың скалярлық көбейтіндісі Вектордың проекциясы. Кеңістікте бағытталған түзуi берілсін. Анықтама. нүктесінің түзуіндегі проекциясы деп нүктесін айтады. Бұл нүк-те нүкте арқылы өтетін түзуіне жүргі-зiлген перпендикуляр жазықтықтың түзуімен қиылысқан нүктесі. Анықтама. вектордың бағытталған түзуіндегі проекциясы деп векторын айтады, мұндағы нүктелерi және нүктелердiң бойындағы сәйкес проекциялары. Бұл проекцияны деп белгi-лейдi. Егер нөлдiк немесе түзуiне болса, онда оның проекциясы нөлдiк вектор болады. Анықтама. Екі вектордың (өспен өстің, вектор мен өстің) арасындағы бұрыш деп, бір вектордың бағытын екінші вектордың бағытына сәйкес келетіндей етіп бұратын ең кіші бұрышын айтады. Осы суреттерден болатыны айқын. Анықтама. вектордың түзуіндегі сандық проекциясы деп, вектордың ұзындығының векторы мен түзудің арасындағы бұрышының косинусына көбейтіндісін айтады, яғни Егер және болса, онда оң және ол вектордың ұзындығына тең, яғни Егер және болса, онда теріс, яғни . Егер немесе болса, онда Сонымен вектордың бағытындағы проекциясы мен оның сандық проекция-сының арасындағы байланыс мына теңдік арқылы беріледі: мұндағы векторы түзудің бірлік векторы. Егер және векторлары бойында жатса, онда оларды былай жазуға болады: мұндағы векторы түзудің бірлік векторы, ол мен сандар. Мына теңдіктің орындалатындығы айқын. Бұл теңдіктен векторларды қосу азайту және сандарды қосуға немесе азайтуға келтіріледі. және векторлардың бойындағы сандық проекцияларының мынадай қасиет-тері бар: 1-қасиет. 2-қасиет. Дәлелдеуі төмендегі суреттен шығады. Олай болса формула бойынша: Тура осылай мына теңдікті дәлелдеуге болады. Өйткені , онда соңғы теңдік бойынша . Енді алдыңғы қасиеттің дұрыстығын дәлелдейік. бұрышы мен түзудің арасындағы бұрыш болсын. а) Егер болса, б) егер болса, Векторлардың скалярлық көбейтіндісі Анықтама. және екі векторлардың скалярлық көбейтіндісі деп, екі вектордың ұзындықтарының көбейтіндісін олардың арасындағы бұрышының косинусына көбейткенге тең санын айтады, яғни Бұл скалярлық көбейтіндіге басқаша да анықтама беруге болады. Анықтама. және екі векторлардың скалярлық көбейтіндісі деп, вектордың ұзындығын вектордың бағытындағы сандық проекциясына көбейтіндісін немесе вектордың ұзындығын вектордың бағытындағы сандық проекциясына көбейтіндісін айтады, яғни Скалярлық көбейтіндінің қасиеттері: орын ауыстыру (коммутативтi) қасиеті үлестірімділік (дистрибутивтi) қасиеті Бірінші қасиет скалярлық көбейтіндінің анықтамасынан тікелей шығады. Екінші қасиеттің дәлелдеуін келтірейік Бұл жерде векторлардың сандық проекцияларының қасиеттерін және векторлардың скалярлық көбейтіндісiнің анықтамасын пайдаландық. Үшінші қасиеттің дәлелдеуі: Осы қасиеттерден мыналар шығады: . Дәріс №3. Векторлардың сызықты тәуелділігі. Векторлардың сызықтық комбинациясы Векторлардың сызықты тәуелділігі. векторлары берілсін. Кез келген мына түрдегі өрнек мұндағы кейбір нақты сандар, векторлардың сызықты комбинациясы деп аталады. векторларды сызықты тәуелді дейді, егер барлығы бірдей нөлге тең емес тұрақты сандар табылып, мына теңдік орындалса Егер бұл теңдік тек үшін ғана орындалса, онда векторларды сызықты тәуелсіз деп атайды. Векторлардың сызықтық комбинациясы. Егер векторлары сызықты тәуелді болса, онда оның біреуі қалғанының сызықты комбинациясы болады. Шынында да болсын, онда екі жағын -ге бөліп, мына өрнекті аламыз Мұндағы … , Бұл теңдік вектордың векторларының сызықты комбинациясы екендігін көрсетеді. Егер векторы векторларының сызықты комбинациясы болса, яғни теңдігі орындалса, онда векторы берілген векторлар арқылы жіктелген деп аталады. Сызықты тәуелді векторларға кез келген екі коллинеарлы және векторлары мысал бола алады, себебі бұл жағдайда , мұндағы қайсiбір нақты сан. Егер және векторлары коллинеарлы болмаса, онда кез келген оларға компланарлы векторы және векторлары арқылы бір мәнді жіктелетіндігі белгілі, яғни Осы теңдіктен кез келген үш компланарлы векторлардың әрқашанда сызықты тәуелділігі шығады. Тура осылай, егер үш компланарлы емес векторлар болса, онда үш өлшемді кеңістіктегі кез келген векторы осы үш вектор бойынша бір мәнді жіктеледі, яғни Осы теңдіктен үш өлшемді кеңістіктегі кез келген төрт вектордың әрқашанда сызықты тәуелділігі шығады. Анықтама. Үш өлшемді кеңістіктің базисі деп осы кеңiстiктiң компланарлы емес белгілі бір ретпен алынған үш векторын айтады. Жазықтықтың базисі деп коллинеарлы емес осы жазықтықтың белгілі бір ретпен алынған екі векторын айтады. Түзудің кез келген нөл емес векторы осы түзудің базисi болады. Дәріс №4.
|
|
|
|
|
|
|
|
|
|
|
|
Векторды базистер бойынша жіктеу
Векторларды санға көбейту. Нөлден өзгеше ɑ векторларының α санына көбейтіндісідеп ұзындығы  -ға тең, α > 0 болғанда ɑ векторымен бағыттас, ал α< 0 болғанда ɑ векторының α санына көбейтіндісі αɑдеп белгіленеді. (сандық көбейткіш сол жағына жазылады).
-ға тең, α > 0 болғанда ɑ векторымен бағыттас, ал α< 0 болғанда ɑ векторының α санына көбейтіндісі αɑдеп белгіленеді. (сандық көбейткіш сол жағына жазылады).
Векторды санға көбейту сандарды көбейту заңдарына бағынады:
1) α 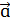 =
= 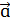 α ; (ауыстырымдылығы);
α ; (ауыстырымдылығы);
2) α(β 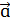 ) = (αβ)
) = (αβ) 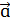 ; (терімділігі);
; (терімділігі);
3) α(  +
+  ) =α
) =α 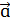 + α
+ α  ;
;
(α + β) 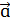 = α
= α 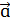 + β
+ β 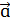 (үлестірімділігі).
(үлестірімділігі).
Егер α 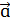 = 0 болса, онда немесе α = 0 немесе ɑ = 0. Коллинеар ɑ және b векторлары үшін әрқашан
= 0 болса, онда немесе α = 0 немесе ɑ = 0. Коллинеар ɑ және b векторлары үшін әрқашан
 = λ
= λ 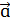
теңдігі орындалатындай λ саны табылады.
Екі вектордың коллинеар болуының қажетті және жеткілікті шарты осы теңдігпен немесе оларды байланыстыратын
α 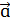 + β
+ β  =0
=0
сызықтық тәуелділігімен өрнектеледі.
Бір жазықтықта жататын немесе оған параллель векторлар компланар векторлар деп аталады. Үш вектордың компланар болуының қажетті және жеткілікті шарты
α 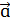 + β
+ β  + γ
+ γ  = 0
= 0
теңдігінде көрінеді, мұнда α,β,γ бір мезгілде нөлгі тең емес. α1, α2, ... , αn сандарына көбейтілген ɑ1, ɑ2, ... , ɑnвекторларының тізбекті түрдегі
α1ɑ1 + α2ɑ2 + ... + αnɑn = 0
қосындысыɑ1, ɑ2, ... , ɑn векторларының сызықтық комбинациясы деп аталады.
Егер
α1 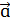 1 + α2
1 + α2 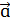 2 + ... + αn
2 + ... + αn 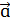 n =
n = 
теңдігі қанағаттандыратын және кемінде біреуі нөлден өзгеше α1 , α2 , ... , αn сандары табылса, онда ɑ1, ɑ2, ... , ɑn векторларын сызықтық тәуелді векторлар дейміз.
Егер (1.7) теңдігі тек қанаα1= α2 = ... =αn = 0 жағдайында орындалса, ɑ1,ɑ2, ... , ɑn векторларын сызықтық тәуелсіз векторлар дейді.
Вектордың базисі бойынша жіктелуі. Векторлық кеңістіктің базисі деп сол кеңістің векторларының төмендегі екі шартты қанағаттандыратын B={e1, e2, e3} реттелген жүйесін айтады:
1) В жүйесінің векторлары сызықтық тәуелсіз.
2) Кеңістіктің кез келген векторы В жүйесі векторларының сызықтық комбинациясы болып табылады.
Базиске кіретін векторларды базистік векторлар дейтін боламыз. Базистік векторлар саны векторлық кеңістіктің өлшемділігі деп аталады. Сонымен, үшөлшемді V3 кеңістігіндегі сызықтық тәуелсіз, базисті құрайтын векторлар үшеу болады, ал кез келген ɑ  V3 векторы олардың сызықтық комбинациясы болып келеді:
V3 векторы олардың сызықтық комбинациясы болып келеді:
ɑ=х1е1 + х2е2 +х3е3 ɑ векторының мұндай түрдегі өрнектелуін оның В базисінің векторлары бойынша жіктелуі дейді. Бұл жіктелудегі х1,х2, х3 сандары ɑ векторының В = (e1, e2, e3) базисіне қатысты анықталатын координаталары деп аталады.
Берілген ɑ векторының В базисі бойынша жіктелуі, атап айтқанда х1,х2, х3 координаталар үштігінің жалғыз болатындығына көз жеткізу қиын емес. Шынында да бұл жіктелуімен қоса мынадай жіктелу де бар делік:
ɑ=у1е1 + у2е2 +у3е3
Онда алдыңғы өрнектен соңғы өрнекті шегеріп, мынаны аламыз:
0 = (х1 – у1)е1 + (х2 – у2)е2 + (х3 – у3)е3,
бұдан e1, e2, e3 векторларының сызықтық тәуелсіздігін ескерсе
х1 – у1=0; х2 – у2=0; х3 – у3=0,
демек екі жіктелу беттеседі.
Сонымен базистің арқасында вектордың берілуі үш скалярдың берілуіне келтіріледі.
Теорема. Векторлар қосындысының координаталары қосылғыштардың сәйкес координаталарының қосындысына тең; векторды санға көбейткенде сол вектордың әрбір координатасы осы санға көбейтіледі.
Дәлелдеуі. ɑ және b векторлары берілсін:
ɑ=х1е1 + х2е2 +х3е3,
b=z1е1 + z2е2 +z3е3.
Сонда
1. ɑ + b = (х1+z1)е1 + (х2+z2)е2 + (х3+z3)е3,
2. λɑ=λ(х1е1 + х2е2 +х3е3).
Мұнда λ  R, ендеше
R, ендеше
λɑ=(λх1)е1 + (λх2)е2 + (λх3)е3
Евклид кеңістігінде өзара перпендикуляр бірлік векторлар үштігі болып келетін декарттық базистер өте қолайлы екенін атап кеткен жөн. Декарттық базистің векторларын i, j, k деп жиі белгілейді.
Әдебиетте вектор координаталарын базистік векторларға параллель болатын, координаталық осьтеріне жасайтын вектордың проекциялары ретінде ұғынады.
Әрбір осьте өзіндік базистік е векторы бар, демек оське параллель болатын әрбір ɑ векторы сәйкес базистік е векторы арқылы ɑ = αе түрінде өрнектеледі.
Бір жағынан кеңістіктің кез келген b векторын кез келген оське проекциялап, оське табылған bʹ векторын b векторының проекциясы деп санауға болады. Бірақ b векторының оське түсетін ортональ проекциясы деп bʹ векторының базистік е векторы арқылы өрнектелетін санын айтқан ыңғайлы:
Преb = α , bʹ = αе
Проекциялар жайлы мынадай тұжырым мәлім: векторлар қосындысының оське түсетін проекциясы қосылғыш векторлардың проекцияларының қосындысына тең:
пре(ɑ1 + ɑ2 + ... + ɑn) = преɑ1 + ... + преɑn
элементар тригонометриядан
Преb = b  ,
, 
маңызды арақатынасы шығады.
Егер вектордың ортональ проекциясы ұғымын жоғарыдағыдай ұғынса, онда вектор координаталары оның осьтерге түсетін проекцияларына тең болатындығы айқын.
Әлбетте егер ɑ = хi + yj + zk болса, онда
x = пpiɑ; y = пpjɑ; z = пpkɑ
Дәріс №5.
Кеңістіктегі тік бұрышты декарттық координаталар жүйесі
Кеңістікте үш координаталық ось өзара тікбұрыш жасап қиылысын. Олардың өлшем бірліктері бірдей болсын. Олардың ортақ қиылысу нүктесін  - мен белгілеп координаталар басы деп атаймыз. Алынған жүйені кеңістіктегі тік бұрышты декарттық координаталар жүйесі деп атаймыз.
- мен белгілеп координаталар басы деп атаймыз. Алынған жүйені кеңістіктегі тік бұрышты декарттық координаталар жүйесі деп атаймыз.

Бірінші координаталық осьті  әріпімен белгілейміз.
әріпімен белгілейміз.  осі немесе абсциссалар осі деп атаймыз.
осі немесе абсциссалар осі деп атаймыз.
Екінші координаталық осьті 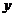 әріпімен белгілейміз.
әріпімен белгілейміз. 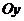 осі немесе ординаталар осі деп атаймыз.
осі немесе ординаталар осі деп атаймыз.
Үшінші координаталық осьті  әріпімен белгілейміз.
әріпімен белгілейміз.  осі немесе аппликаталар осі деп атаймыз.
осі немесе аппликаталар осі деп атаймыз.
Кеңісітіктегі тік бұрышты декарттық координаталар жүйесі кеңістікті сегіз бөлікке бөледі. Оларды октанта деп атаймыз. Октантадағы таңбалар:
І октантада  > 0, > 0, 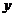 > 0, > 0,  > 0 > 0
| ІІ октантада  < 0, < 0, 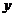 > 0, > 0,  > 0 > 0
|
ІІІ октантада  < 0, < 0, 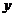 < 0, < 0,  > 0 > 0
| ІҮ октантада  > 0, > 0, 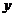 < 0, < 0,  > 0 > 0
|
Ү октантада  > 0, > 0, 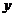 > 0, > 0,  < 0 < 0
| ҮІ октантада  < 0, < 0, 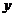 > 0, > 0,  < 0 < 0
|
ҮІІ октантада  < 0, < 0, 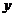 < 0, < 0,  < 0 < 0
| ҮІІІ октантада  > 0, > 0,  < 0, < 0,  < 0 < 0
|

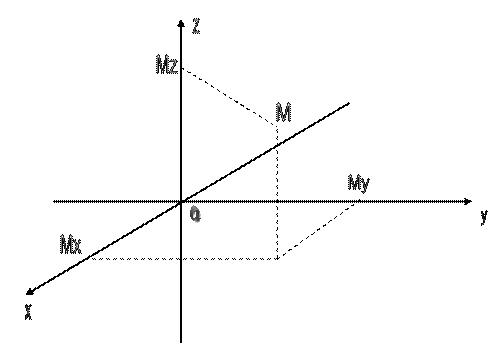
Кеңістікте кез- келген  нүктесі берілсін. Осы
нүктесі берілсін. Осы  нүктесі арқылы
нүктесі арқылы  осіне перпендикуляр жазықтық жүргізсек, ол
осіне перпендикуляр жазықтық жүргізсек, ол  осін бір нүктеде қияды. Ол нүктені
осін бір нүктеде қияды. Ол нүктені  нүктесі деп белгілейміз. Дәл осылай қалған осьтерге де перпендикуляр жазықтықтар жүргіземіз. Олар да сәйкесінше
нүктесі деп белгілейміз. Дәл осылай қалған осьтерге де перпендикуляр жазықтықтар жүргіземіз. Олар да сәйкесінше  осінен және
осінен және  осінен
осінен  және
және  нүктелерін қиып өтеді. Сонда
нүктелерін қиып өтеді. Сонда  ,
,  ,
,  шамаларын
шамаларын  нүктесінің кеңістіктегі тікбұрышты декарттық координаталары деп атаймыз және келесі символмен белгілейміз:
нүктесінің кеңістіктегі тікбұрышты декарттық координаталары деп атаймыз және келесі символмен белгілейміз:  . Мұндағы
. Мұндағы  ,
,  ,
,  .
.
Дәріс №6.
Координаттары берілген векторларға қолданылатын сызықтық амалдар
Кеңістіктегі үшөлшемді декарттық координаталар жүйесінде кез келген  нүктесі берілсін. Бағытталған
нүктесі берілсін. Бағытталған  кесіндісі
кесіндісі  нүктесінің радиус-векторы деп аталады.
нүктесінің радиус-векторы деп аталады. 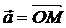 радиус-векторының координаталар осьтеріндегі сандық проекциялары
радиус-векторының координаталар осьтеріндегі сандық проекциялары  деп белгіленген. Бұл
деп белгіленген. Бұл  сандары
сандары  нүктесінің координаттары;
нүктесінің координаттары;  – абсцисса,
– абсцисса,  – ордината,
– ордината,  – аппликата деп аталады. Сонымен
– аппликата деп аталады. Сонымен 
 векторының
векторының  осіндегі,
осіндегі, 
 осіндегі, ал
осіндегі, ал 
 осіндегі проекциясы болса, онда
осіндегі проекциясы болса, онда  деп жазылады.
деп жазылады.
 және
және 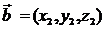 векторлары берілсін. Онда мына үш теңдік дұрыс:
векторлары берілсін. Онда мына үш теңдік дұрыс:

| |

| |

|
теңдіктің дұрыстығы, векторлардың анықтамасынан шығады. Векторларға қолданылатын сызықтық амалдар, олардың проекцияларына да қолданылады, сондықтан теңдіктер дұрыс.
 координат өстерінің бірлік векторлары болғандықтан мына теңдіктер дұрыс:
координат өстерінің бірлік векторлары болғандықтан мына теңдіктер дұрыс:
|
| |
 , , 
| |
Кез келген  векторын былай жазуға болады
векторын былай жазуға болады

|
формулалардан


 және
және  векторлары берілсін. Онда
векторлары берілсін. Онда

|
шынында да, формулаларды пайдаланып

 Егер
Егер 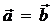 болса, яғни
болса, яғни  , онда
, онда
| | ||
| Вектордың ұзындығы (модулі) оның сандық проекцияларының квадраттарының қосындысының квадрат түбіріне тең. Бұл формуламен кеңістікте берілген екі нүктенің –
Себебі бұл арақашықтық | ||
|
| ||
| | ||
формуладан мынандай тұжырым шығады:

|
Мұндағы 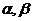 және
және  - бұрыштары
- бұрыштары  векторымен координат өстерінің арасындағы сәйкес бұрыштары.
векторымен координат өстерінің арасындағы сәйкес бұрыштары.
Егер  векторы
векторы  вектордың бірлік векторы болса, онда
вектордың бірлік векторы болса, онда 
Мысал.  және
және  векторлары берілсін.
векторлары берілсін.
 векторының координаттарын табу керек.
векторының координаттарын табу керек.
Шешуі. 
Дәріс №7.
Координаттары берілген векторлардың скалярлық көбейтіндісі, векторлардың арасындағы бұрыш
Скаляр көбейтіндінің координаттық түрі. Декарттық координаталар жүйесінде  және
және  векторлары берілсін.
векторлары берілсін.
Егер  орттары үшін, скаляр көбейтіндінің анықтамасын қолдансақ,
орттары үшін, скаляр көбейтіндінің анықтамасын қолдансақ,

болатындығын оңай байқауға болады.
Теорема. Егер  және
және  векторлары координаталар арқылы берілген болса, онда олардың скаляр көбейтіндісі
векторлары координаталар арқылы берілген болса, онда олардың скаляр көбейтіндісі

теңдігімен анықталады.
Дәлелденуі. Айталық  ,
,  векторлары берілсін, мұндағы
векторлары берілсін, мұндағы 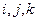 -тік бұрышты декарттық координаталар жүйесінің жоғарыдағы теңдіктерді қанағаттандыратын орттар. Сонымен
-тік бұрышты декарттық координаталар жүйесінің жоғарыдағы теңдіктерді қанағаттандыратын орттар. Сонымен

Теорема дәлелденді.
Дербес жағдайда,


Жоғарыда дәлелденген теоремаларды пайдаланып екі вектордың ортоганалдық (перпендикулярлық) шартын алуымызға болады,

Скаляр көбейтіндінің координаттық түрін пайдаланып, олардың арасындағы бұрыштың косинусын және векторлардың бір-біріне проекцияларының формулаларын аламыз:


Анықтама.  векторының координат осьтерімен жасайтын
векторының координат осьтерімен жасайтын  бұрыштарының косинустары
бұрыштарының косинустары  векторының бағыттаушы косинустары деп аталынады.
векторының бағыттаушы косинустары деп аталынады.

екендігі шығады. Демек, вектордың бағыттаушы косинустарының квадраттарының қосындысы бірге тең, яғни  Олай болса, вектордың бағыттаушы косинустары бірлік вектордың координаталары болады:
Олай болса, вектордың бағыттаушы косинустары бірлік вектордың координаталары болады:

1-мысал.  және
және  векторларының скаляр көбейтіндісін табу керек.
векторларының скаляр көбейтіндісін табу керек.
 = {1, -5, 12},
= {1, -5, 12},  = {1, 5, 2}.
= {1, 5, 2}.
Шешуі:  = 1·1 + (-5) ·5 + 12·2 = 1 – 25 + 24 = 0, яғни
= 1·1 + (-5) ·5 + 12·2 = 1 – 25 + 24 = 0, яғни  және
және  векторлары ортогональды.
векторлары ортогональды.
2-мысал.  және
және  векторларының арасындағы φ бұрышын табыңыз.
векторларының арасындағы φ бұрышын табыңыз.
Шешуі:  ,
,
бұдан  .
.
3-мысал.  және
және  векторларының арасындағы бұрышты табу керек.
векторларының арасындағы бұрышты табу керек.
Шешуі:  болғандықтан,
болғандықтан,  . Мұндағы
. Мұндағы  ,
,  ,
,  . Сондықтан,
. Сондықтан,  және
және  .
.
Дәріс №8.
Векторлардың коллинеар және ортогонал болу шарттары
Егер  және
және  векторлары коллинеарлы болса, онда оларды былай жазуға болады
векторлары коллинеарлы болса, онда оларды былай жазуға болады  мұндағы
мұндағы 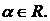 Олай болса
Олай болса  онда
онда  яғни
яғни

|
Бұл формуланы векторлардың коллинеар болу шарттары деп атайды.
Егер формуланың бөлімдерінің біреуі немесе екеуі нөл болса, онда оны нөлге бөлу деп түсінуге болмайды, олай жазылу векторлардың коллинеар болуының символикалық жазылуы деп түсіну керек.
Мысал:  және
және  векторлары коллинеар, себебі олардың координаттары жоғарыдағы шартты қанағаттандырады.
векторлары коллинеар, себебі олардың координаттары жоғарыдағы шартты қанағаттандырады.
 олай болса
олай болса 
Егер  және
және  перпендикуляр векторлар болса, онда олардың скалярлық көбейтіндісі нөлге тең, яғни
перпендикуляр векторлар болса, онда олардың скалярлық көбейтіндісі нөлге тең, яғни  Осыдан
Осыдан
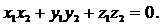
|
формуланы векторлардың перпендикуляр болу немесе ортогонал болу шарты деп атайды.
Екі векторлардың скалярлық көбейтіндісінен екі векторлардың арасындағы бұрышты анықтауға болады. Скалярлық көбейтіндінің бірінші анықтамасынанан

|
Скалярлық көбейтіндінің екінші анықтамасынан 

| |

|
Мысал:  күштің түзудің бойымен денені
күштің түзудің бойымен денені  нүктеден
нүктеден  нүктеге жылжытқандағы жұмысты есептеу керек және
нүктеге жылжытқандағы жұмысты есептеу керек және  күші
күші  - ға қандай бұрышпен бағытталғандығын табу керек.
- ға қандай бұрышпен бағытталғандығын табу керек.
 Шешуі:Материалдық нүкте түзудің бойымен
Шешуі:Материалдық нүкте түзудің бойымен  күштің әсерінен күштің әсерінен  нүктеден нүктеден  нүктеге жылжысын. нүктеге жылжысын.  күші мен күші мен  векторының арасындағы бұрыш векторының арасындағы бұрыш  болсын. Онда болсын. Онда  күшінің күшінің  бойындағы жасаған жұмысы мынаған тең: бойындағы жасаған жұмысы мынаған тең:
 яғни яғни 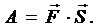
|
Сонымен тұрақты күштің жұмысы күш векторы мен жол векторының скалярлық көбейтіндісіне тең.
 , олай болса
, олай болса  (жұмыс бірлігі).
(жұмыс бірлігі).
 және
және  арасындағы
арасындағы  бұрышты мына формуламен табамыз
бұрышты мына формуламен табамыз
 ,
,  ,
,  .
.
Берілген екі векторға ортогональ вектор. Алдағы уақытта жиі қолданылатын есепті қарастырайық.
Айталық өзара коллинеарлы емес екі  және
және  векторлары берілсін. Мақсатымыз – осы векторларға ортогональ болатын
векторлары берілсін. Мақсатымыз – осы векторларға ортогональ болатын  векторын табу.
векторын табу.
Ол үшін жоғарыдағы екі вектордың ортогоналдық шартын пайдаланамыз:

Біз үш белгісізді екі теңдеулер жүйесін алдық. Егер белгісіздердің біреуінің коэффициенті нөлден ерекше болса, мысал үшін  , онда бірінші теңдеуден
, онда бірінші теңдеуден  -ті тауып,
-ті тауып,  екіншісіне қойсақ,
екіншісіне қойсақ,

болатындығын көреміз. Демек

Бұдан үшінші айнымалы  -ке кез келген мән беру арқылы, берілген
-ке кез келген мән беру арқылы, берілген  және
және  векторына ортогональ болатын сансыз көп
векторына ортогональ болатын сансыз көп  векторларын аламыз және олардың барлығы өзара коллинеарлы болады. Сондықтан, дербес жағдайда,
векторларын аламыз және олардың барлығы өзара коллинеарлы болады. Сондықтан, дербес жағдайда, 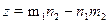 деп алсақ,
деп алсақ,

берілген векторларға ортогональ векторды аламыз.
Енді екінші ретті анықтауышты пайдаланып

болатындығын көреміз. Ендеше
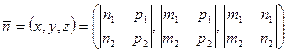
Дәріс №9.
Векторлардың векторлық көбейтіндісі және оның қасиеттері
Анықтама. Бас нүктелері бір нүктеге орналасқан ортонормалданған  және
және  векторлар үштігін оң (теріс) дейміз, егер де
векторлар үштігін оң (теріс) дейміз, егер де  вектордың соңғы нүктесінен қарағанда
вектордың соңғы нүктесінен қарағанда  векторнан
векторнан  векторына бұрылатын ең кіші бұрыш сағат тіліне қарсы (сағат тіліне бағыттас) бағытта көрінсе.
векторына бұрылатын ең кіші бұрыш сағат тіліне қарсы (сағат тіліне бағыттас) бағытта көрінсе.
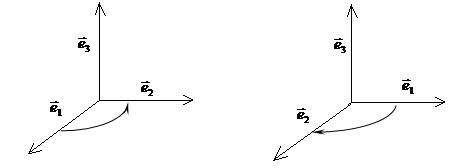
оң үштік теріс үштік
Кез келген компланарлы емес  векторлар үштiгiнен алты үштiк құруға болады
векторлар үштiгiнен алты үштiк құруға болады
 , ,  , , 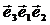 , ,  , ,  , , 
|
бiрiншi үштiк оң болса, онда қатар тұрған үш үштiк оң болады, ал қалған үш үштiк теріс болады.
Координаттар жүйесiн оң (теріс) деп атайды, егер олардың базистерi  оң (теріс) үштiк құрса.
оң (теріс) үштiк құрса.
Анықтама.Екi  мен
мен  векторларының векторлық көбейтiндiсiдеп келесi үш шартты қанағаттандыратын қандай да бір
векторларының векторлық көбейтiндiсiдеп келесi үш шартты қанағаттандыратын қандай да бір  векторын айтады:
векторын айтады:

|  , , 
|

| 
|

|  үштiгi оң үштiк құрайды. үштiгi оң үштiк құрайды.
|
Векторлық көбейтiндiнi 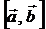 немесе
немесе  деп белгiлейдi.
деп белгiлейдi.
Векторлық көбейтiндiнiң кейбiр қасиеттерi:
1-қасиет.  вектордың ұзындығы, бас нүктелерi бiр нүктеге орналасқан вектордың ұзындығы, бас нүктелерi бiр нүктеге орналасқан  мен мен  векторларынан құрылған параллелограммның ауданына тең. Бұл бiрiншi шарттан және суреттен шығады. векторларынан құрылған параллелограммның ауданына тең. Бұл бiрiншi шарттан және суреттен шығады.
|
|
2-қасиет.Векторлық көбейтiндi нөлге тең сонда, тек сонда ғана, егерде  мен мен  векторлары коллинеарлы болса немесе екеуiнiң бi реуi нөлдiк вектор болса. векторлары коллинеарлы болса немесе екеуiнiң бi реуi нөлдiк вектор болса.
| |
3-қасиет.  көбейткiштердiң орнын ауыстырғанда көбейтiндi таңбасын өзгертедi. көбейткiштердiң орнын ауыстырғанда көбейтiндi таңбасын өзгертедi.  және және 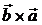 векторлары коллинеарлы ұзындықтары бірдей, олай болса параллелограммның ауданы өзгермейді. Бірақ үшінші шартты қанағаттандыру үшін векторлары коллинеарлы ұзындықтары бірдей, олай болса параллелограммның ауданы өзгермейді. Бірақ үшінші шартты қанағаттандыру үшін  вектордың бағытын қарама-қарсы бағытқа өзгерту керек. Сондықтан вектордың бағытын қарама-қарсы бағытқа өзгерту керек. Сондықтан  .
4-қасиет. .
4-қасиет. 

 , , 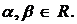
|

|
Бұл қасиеттер векторлық көбейтіндінің анықтамасынан шығады.
5-қасиет. 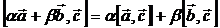
Векторлық көбейтiндiнiң бұл үлестірімділік заңын кейін (12-дәрісте) дәлелдейміз.
Үш вектордың екі еселі векторлық көбейтіндісі. Үш вектордың екі еселі векторлық көбейтіндісі деп, екі вектордың векторлық көбейтіндісін үшінші векторға векторлық көбейткенді айтады да, былай белгілейді  .
.
Екі еселі векторлық көбейтіндіні табу үшін, оны үш вектордың көбейтіндісінің бірінші түріне келтіру формулаларын пайдаланады, яғни
 немесе
немесе  .
.
Дәріс №10.
Координаттары берілген векторлардың векторлық көбейтіндіcі
Теорема. Егер тік бұрышты координаттар системасында  және
және 
 векторлары координаталары арқылы берілген болса, онда сол системадағы векторлық көбейтіндінің сызықтық жіктелуі мына түрде болады:
векторлары координаталары арқылы берілген болса, онда сол системадағы векторлық көбейтіндінің сызықтық жіктелуі мына түрде болады:
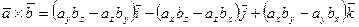
Бұл өрнекті символды түрде үшінші ретті анықтауыш арқылы былай жазады:

Анықтауышты бірінші жатық жолы бойынша жіктесек, төмендегіше болады:

Дәлелдеуі. Базистік  векторлардың анықтамасы бойынша және векторлық көбейтіндінің 1 және 3-қасиеттерін пайдалансақ, мынадай теңдіктерді аламыз:
векторлардың анықтамасы бойынша және векторлық көбейтіндінің 1 және 3-қасиеттерін пайдалансақ, мынадай теңдіктерді аламыз:

Енді 4-қасиетті және жоғарыдаға алынған теңдіктерді ескерсек мына формуланы аламыз:

Екі векторлық көбейтіндісінің 2-қасиетін пайдалансақ, екі вектордың коллинеарлық шарты былай жазылады:
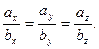
Координаталарымен берілген векторлардың векторлық көбейтіндісіне жаттығу орындайық.
1-мысал. 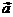 = {3, -4, 2} және
= {3, -4, 2} және  = {1, 5, 1}векторларының векторлық көбейтіндісін табу керек
= {1, 5, 1}векторларының векторлық көбейтіндісін табу керек
Шешуі:  =
=  ={-14, -1, 19}.
={-14, -1, 19}.
2-мысал.  және
және  векторларының векторлық көбейтіндісін табу керек.
векторларының векторлық көбейтіндісін табу керек.
Шешуі:  , яғни
, яғни  .
.
Дәріс №11.
Векторлық көбейтіндінің қолданылуы
Векторлық көбейтiндiнiң 1-қасиетi бойынша  вектордың модулі бас нүктелерi бiр нүктеге орналасқан
вектордың модулі бас нүктелерi бiр нүктеге орналасқан  мен
мен  векторларынан құрылған параллелограммның ауданына тең. Осы қасиеттің қалай қолданылатынын қарастырайық.
векторларынан құрылған параллелограммның ауданына тең. Осы қасиеттің қалай қолданылатынын қарастырайық.
1-мысал. Төбелері  болатын үшбұрыштың ауданын және
болатын үшбұрыштың ауданын және  қабырғасына түсірілген биіктігінің ұзындығын есептеу керек.
қабырғасына түсірілген биіктігінің ұзындығын есептеу керек.

Шешуі.  үшбұрышының ауданы
үшбұрышының ауданы  параллелограмның ауданының жартысына тең болғандықтан: ол үшбұрыштың ауданы
параллелограмның ауданының жартысына тең болғандықтан: ол үшбұрыштың ауданы  және
және  векторларының векторлық көбейтіндісінің модулінің жартысына тең болады:
векторларының векторлық көбейтіндісінің модулінің жартысына тең болады:



Бұл векторлардың векторлық көбейтіндісін формула бойынша есептейміз.

Үшбұрыштың ауданын  формуласына
формуласына  биіктігін табамыз:
биіктігін табамыз:

Жауабы.  ауд. бірл.,
ауд. бірл.,  ұз. бірл.
ұз. бірл.
2-мысал. 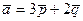 және
және  векторлары берілген. Мұнда
векторлары берілген. Мұнда  .
.  мен
мен  векторлары арқылы тұрғызылған параллелограмның ауданын табу керек.
векторлары арқылы тұрғызылған параллелограмның ауданын табу керек.
Шешуі. Векторлық көбейтіндінің анықтамасын және қасиеттерін пайдаланамыз:

Жауабы.  ауд. бірл.
ауд. бірл.
3-мысал.  және
және  векторлары
векторлары  мен
мен  қандай мәндерінде коолинеар болады?
қандай мәндерінде коолинеар болады?
Шешуі. Екі вектор коллинеар боу үшін оның сәйкес координаталары пропоционал болуы қажет: 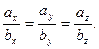
Демек 
Дәл сол сияқты 
Жауабы.  .
.
4-мысал. Егер  және
және  болса, онда
болса, онда  және
және  векторлары коллинеар бола ма?
векторлары коллинеар бола ма?
Шешуі.  және
және  векторларының координатасын берілген амалдарды орындап табайық:
векторларының координатасын берілген амалдарды орындап табайық:
 =4(-1, 2, 8)-3(3, 7, 1)=(-4, 8, 32)-(9, 21, -3)=(-13, -13, 36),
=4(-1, 2, 8)-3(3, 7, 1)=(-4, 8, 32)-(9, 21, -3)=(-13, -13, 36),
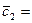 9(3, 7, -1)-12(-1, 2, 8)=(37, 63, -9)-(-12, 24, 96)=(39, 39, -105).
9(3, 7, -1)-12(-1, 2, 8)=(37, 63, -9)-(-12, 24, 96)=(39, 39, -105).
Сәйкес координаталары  пропоционал болғандықтан
пропоционал болғандықтан  және
және  векторлары өзара коллинеар.
векторлары өзара коллинеар.
Жауабы.Векторлар коллинеарболады.
Дәріс №12.
Векторлардың аралас көбейтіндісі және қасиеттері
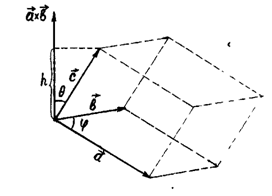
 кеңістігіндегі әрбір компланарлы емес бастары бір нүктеге орналасқан кез келген үш вектор параллелепипедті анықтайды. Осы үш векторлар параллелепипедтің қырларын құрай-ды. Параллелепипедтті оң (теріс) бағыт-талған дейді, егерде кеңістігіндегі әрбір компланарлы емес бастары бір нүктеге орналасқан кез келген үш вектор параллелепипедті анықтайды. Осы үш векторлар параллелепипедтің қырларын құрай-ды. Параллелепипедтті оң (теріс) бағыт-талған дейді, егерде  векторлары оң (сол) үштік құрайтын болса. векторлары оң (сол) үштік құрайтын болса.
| 
|
Анықтама: Кез келген  векторлары берілсін. Егер
векторлары берілсін. Егер  векторын
векторын  векторына векторлық көбейтіп, содан кейін
векторына векторлық көбейтіп, содан кейін  векторын
векторын  векторына скаляр көбейтсек нәтижесінде
векторына скаляр көбейтсек нәтижесінде  векторларының аралас көбейтіндісі деп аталатын
векторларының аралас көбейтіндісі деп аталатын  саны шығады.
саны шығады.
Үш вектордың аралас көбейтіндісін  ,
, 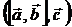 немесе
немесе  символдарымен белгілейміз.
символдарымен белгілейміз.
Аралас көбейтіндінің кейбір қасиеттері:
1-қасиет.  аралас көбейтінді
аралас көбейтінді  және
және  векторларынан құрылған бағытталған параллелепипедтің көлеміне тең. Егер
векторларынан құрылған бағытталған параллелепипедтің көлеміне тең. Егер  үштігі оң болса, оң таңба-мен, ал
үштігі оң болса, оң таңба-мен, ал  үштiгi сол болса, теріс таңбамен алынған осы параллелепипедтің көлеміне тең.
үштiгi сол болса, теріс таңбамен алынған осы параллелепипедтің көлеміне тең.
Шынында да, параллелепипедтің табаны  және
және  векторларынан құрылған параллелограмм болады. Оның ауданы
векторларынан құрылған параллелограмм болады. Оның ауданы  . Параллелепипедтің биіктігі
. Параллелепипедтің биіктігі  ,
,  дегеніміз
дегеніміз  Олай болса параллелепипедтің көлемі
Олай болса параллелепипедтің көлемі

|
Егер  оң үштік құрса,онда
оң үштік құрса,онда 
 ал егер сол үштік болса, онда
ал егер сол үштік болса, онда 
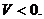
2-қасиет. Егер  векторлары компланарлы болса, онда аралас көбейтінді нөлге тең.
векторлары компланарлы болса, онда аралас көбейтінді нөлге тең.
Шынында да, егер  немесе
немесе  болса,
болса, 
 аралас көбейтінді нөлге тең.
аралас көбейтінді нөлге тең.  болса
болса  векторы
векторы 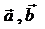 векторлары жатқан жазықтықта жатады, ал
векторлары жатқан жазықтықта жатады, ал  болса, онда
болса, онда  және
және  векторлары коллинеарлы болады. Сондықтан
векторлары коллинеарлы болады. Сондықтан  векторлары осы екі жағдайда да компланарлы болады. Сонымен
векторлары осы екі жағдайда да компланарлы болады. Сонымен

|
теңдігі үш вектордың компланарлы болу шарты.
3-қасиет. Егер аралас көбейтіндінiң көбейткіштерiн циклдiк орын алмастырсақ оның мәнi өзгермейді

|
Шынында да 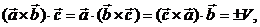 ал оң жақтағы таңба бірдей, себебі
ал оң жақтағы таңба бірдей, себебі  - үштіктер бірдей бағытталған.
- үштіктер бірдей бағытталған.
| Салдар. | 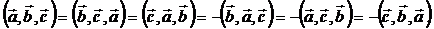
|
4- қасиет. Аралас көбейтіндінің сызықтық қасиеті.
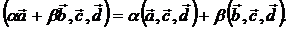
|
Бұл теңдіктің дәлелдеуі 3-қасиетінен және скалярлық көбейтіндінің сызықтық қасиетінен шығады.
Енді векторлық көбейтіндінің 5-ші қасиетін дәлелдейік:

|
Аралас көбейтіндінің 3-ші және 4-ші қасиеттерінен

Осыдан формуланың дұрыстығы шығады, яғни
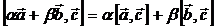
Дәріс №13.
Координаттары берілген векторлардың аралас көбейтіндіcі
Теорема. Тікбұрышты координаттар системасында  ,
,  және
және  векторларының координаталары белгілі болса, онда олардың аралас көбейтіндісі сол векторлардың координаталарынан құралған үшінші ретті анықтауышқа тең болады:
векторларының координаталары белгілі болса, онда олардың аралас көбейтіндісі сол векторлардың координаталарынан құралған үшінші ретті анықтауышқа тең болады:
 .
.
Дәлелдеуі.  болғандықтан, екі вектордың векторлық көбейтіндісі бойынша:
болғандықтан, екі вектордың векторлық көбейтіндісі бойынша:
 .
.
Енді  векторын
векторын  векторына скаляр көбейтсек:
векторына скаляр көбейтсек:
 .
.
Сонда бізге  және
және  векторлары берілсін. Онда жоғарыдағы формуланы пайдаланып және векторлық көбейтіндінің қасиеттерінен мына өрнекті аламыз
векторлары берілсін. Онда жоғарыдағы формуланы пайдаланып және векторлық көбейтіндінің қасиеттерінен мына өрнекті аламыз
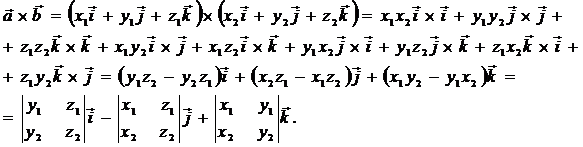
|
Бұл формуланы үшінші ретті анықтауыш түрінде де жазуға болады
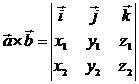
|
Егер  болса, онда аралас көбейтіндінің анықтамасы бойынша осы формуланы пайдаланып мына өрнекті аламыз
болса, онда аралас көбейтіндінің анықтамасы бойынша осы формуланы пайдаланып мына өрнекті аламыз
 . .
|
Координаталарымен берілген векторлардың аралас көбейтіндісіне жаттығу орындайық.
1-мысал.  = {-3, 2, -1},
= {-3, 2, -1},  {2, 1, 0},
{2, 1, 0},  = {-1, 3, -1} векторларының аралас көбейтіндісін табу керек.
= {-1, 3, -1} векторларының аралас көбейтіндісін табу керек.
Шешуі:  =
=  векторлар компланар.
векторлар компланар.
2-мысал. 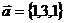 ,
,  ,
,  векторларын компланарлыққа тексеру керек.
векторларын компланарлыққа тексеру керек.
Шешуі:

Демек  векторлары компланар емес.
векторлары компланар емес.
3-мысал.  ,
,  ,
,  векторларының аралас көбейтіндісін табу керек.
векторларының аралас көбейтіндісін табу керек.
Шешуі: 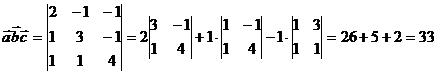 .
.
4-мысал. 
 ,
,  векторлары компланар екенін дәлелдеу керек.
векторлары компланар екенін дәлелдеу керек.
Шешуі: Векторлардың аралас көбейтіндісін табамыз:
 .
.
 болғандықтан,
болғандықтан,  векторлары компланар.
векторлары компланар.
Дәріс №14.
Векторлардың аралас көбейтіндіcінің қолданылуы
 және
және  векторларынан құрылған бағытталған параллелепипедтің
векторларынан құрылған бағытталған параллелепипедтің
көлемі, аралас көбейтіндінің анықтамасы бойынша былай анықталады
 . .
|
Бұл формуладағы анықтауыштың бірінші жолы  векторының, екінші жолы
векторының, екінші жолы  векторының ал үшінші жолы
векторының ал үшінші жолы  векторының координаттары.
векторының координаттары.
1-мысал. Төбелері  және
және  болатын пирамиданың көлемін табу керек.
болатын пирамиданың көлемін табу керек.
Шешуі. Алдымен  және
және  векторларын тұрғызылған параллелепипедтің көлемін аралас көбейтінің анықтамасы бойынша мына формуламен табамыз:
векторларын тұрғызылған параллелепипедтің көлемін аралас көбейтінің анықтамасы бойынша мына формуламен табамыз:
 . .
|
Ал үшбұрышты пирамиданың көлемі
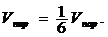
Алдымен  және
және  векторлардың координаттарын табамыз. Сонымен
векторлардың координаттарын табамыз. Сонымен
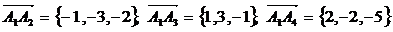
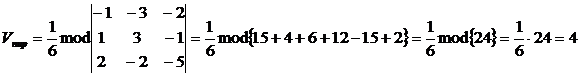 .
.
Жауабы:  көлем бірлігі.
көлем бірлігі.
2-мысал. Төбелері  нүктелері болатын пирамиданың
нүктелері болатын пирамиданың  төбесінен түсірілген биіктігін есептеңдер.
төбесінен түсірілген биіктігін есептеңдер.

Шешуі: Бұл пирамида  векторларына құрылған деп алып, осы үш вектордың аралас көбейтіндісін табамыз, ол санның модулі параллелепипедтің көлемі болады. Ал пирамида көлемі параллелепипедтің көлемінің
векторларына құрылған деп алып, осы үш вектордың аралас көбейтіндісін табамыз, ол санның модулі параллелепипедтің көлемі болады. Ал пирамида көлемі параллелепипедтің көлемінің  болады.
болады.
 векторларының аралас көбейтіндісін есептейік.
векторларының аралас көбейтіндісін есептейік.
 , параллелепипедтің көлемі осы санның
, параллелепипедтің көлемі осы санның  бөлігіне тең болады, яғни
бөлігіне тең болады, яғни  көлем бірлігіне тең болады.
көлем бірлігіне тең болады.
Енді биіктік түсіп тұрған 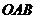 үшбұрышының ауданын есептейік:
үшбұрышының ауданын есептейік:
 (аудан бірлігі).
(аудан бірлігі).
Пирамида көлемі табан ауданы мен биіктігінің көбейтіндісінің  бөлігіне тең, олай болса
бөлігіне тең, олай болса  формуласымен есептеледі:
формуласымен есептеледі:  (ұзындық бірлігі).
(ұзындық бірлігі).
Жауабы:  ұз. бірл.
ұз. бірл.
Дәріс №15.
Екі нүктенің ара қашықтығы. Кесіндіні берілген қатынаста бөлу
Кеңістіктегі тік бұрышты декарттық координаталар үшін  және
және  нүктелерінің арақашықтығы
нүктелерінің арақашықтығы

формуласымен есептеледі.
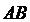 кесіндіні берілген
кесіндіні берілген  қатнаста бөлетін
қатнаста бөлетін  нүктенің координаталарын табу керек, яғни
нүктенің координаталарын табу керек, яғни

Егер дұрыстығы шығады.
|  


 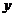

|
болғандықтан, бұл формуладан




Соңғы теңдіктің координаттарын теңестіріп теңдеулер жүйесін аламыз:
  
|
Соңғы формулалар кесіндіні берілген қатынаста бөлу формулалары деп аталады. Дербес жағдайда  болғанда,
болғанда, 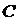 нүктесі кесіндінің ортасында жатса, оның түрі мынандай болады:
нүктесі кесіндінің ортасында жатса, оның түрі мынандай болады:
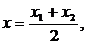   . .
|
Аналитикалық геометрияның есебіне мысалдар келтірейік.
1-мысал.Төбелері  ,
,  ,
,  болатын үшбұрыш тікбұрышты болатынын дәлелдеу керек.
болатын үшбұрыш тікбұрышты болатынын дәлелдеу керек.
Шешуі: Үшбұрыш қабырғаларының ұзындықтарын табамыз:
 ,
,
 ,
,
 .
.
 ,
,  ,
, 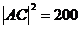
 , яғни үшбұрыштың екі қабырғасы квадраттарының қосындысы үшінші қабырға квадратына тең. Бұдан
, яғни үшбұрыштың екі қабырғасы квадраттарының қосындысы үшінші қабырға квадратына тең. Бұдан  – тікбұрышты, ал АС оның гипотенузасы екендігі шығады.
– тікбұрышты, ал АС оның гипотенузасы екендігі шығады.

2-мысал.АВ кесіндісінің ұштары  ,
,  екені белгілі. Осы кесіндінің бойынан А-ға дейінгі қашықтығы
екені белгілі. Осы кесіндінің бойынан А-ға дейінгі қашықтығы  -ға дейінгі қашықтығынан 2 есе үлкен болатын С нүктесін белгілейік. С нүктесінің координаттарын табу керек.
-ға дейінгі қашықтығынан 2 есе үлкен болатын С нүктесін белгілейік. С нүктесінің координаттарын табу керек.
 Шешуі:
Шешуі: 
 ,
,  , яғни
, яғни 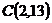
Дата добавления: 2018-06-27; просмотров: 7687; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 ,
,  ,
,  ,
, 



 мен
мен  нүктелерінің арақашықтығын табуға болады.
нүктелерінің арақашықтығын табуға болады.
 және
және  векторлардың ұштарының ара қашықтығына тең. Сонымен суреттен
векторлардың ұштарының ара қашықтығына тең. Сонымен суреттен


 және
және  болса,
болса,  нүктенің белгісіз
нүктенің белгісіз  және
және  координаттарын табу керек. Суреттен және формуладан
координаттарын табу керек. Суреттен және формуладан
