Составление алгоритма, отладка и тестирование программы с использованием рекурсивных подпрограмм

⇐ ПредыдущаяСтр 2 из 10Следующая ⇒

Цель работы: Получить навыки в составлении алгоритма и отладке программы решения задач с использованием подпрограмм.

Теоретические положения

В программировании рекурсия— вызов функции /процедуры из неё же самой, непосредственно (прямая рекурсия) или через другие функции (косвенная рекурсия).

Глубиной рекурсии называется количество вложенных вызовов функции или процедуры. Число рекурсивных вызовов в каждый конкретный момент времени называется текущим уровнем рекурсии.

Компилятор формирует сегмент кода, сегмент данных и сегмент стека.

Динамическая память

Сегмент стека (для хранения локальных данных)

Сегмент данных (для хранения глобальных данных и локальных констант)

Сегмент кода ( код программы в машинных кодах)

Стек (англ. stack — стопка) — структура данных, в которой доступ к элементам организован по принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»)

Для отслеживания точек возврата из подпрограмм используется стек вызовов.

Реализация рекурсивных вызовов функций опирается на механизм стека вызовов: адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. При повторном вызове этот процесс повторяется. Для завершения вычисления каждая рекурсивная программа должна содержать хотя бы одну нерекурсивную ветвь алгоритма, заканчивающуюся возвратом в вызывающую программу.

Любая рекурсивная процедура Rec включает в себя некоторое множество операторов S и один или несколько операторов рекурсивного вызова Р.

Структура рекурсивной процедуры может принимать три формы:

Procedure Rec; Begin S; If условие then Rec; End;

Форма с выполнением действий до рекурсивного вызова ( свыполнением действий на рекурсивном спуске)

2) Форма с выполнением действий после рекурсивного вызова (с выполнением действий на рекурсивном возврате)

Procedure Rec; Begin If условие then Rec; S; End;

3) Форма с выполнением действий до и после рекурсивного вызова ( свыполнением действий как на рекурсивном спуске, так и на рекурсивном возврате)

Procedure Rec; Begin S1; If условие then Rec; S2; End;

или

Procedure Rec; Begin If условие then Begin S1; Rec; S2; End; End;

Задача 1:Используя рекурсивную процедуру, вычислить сумму

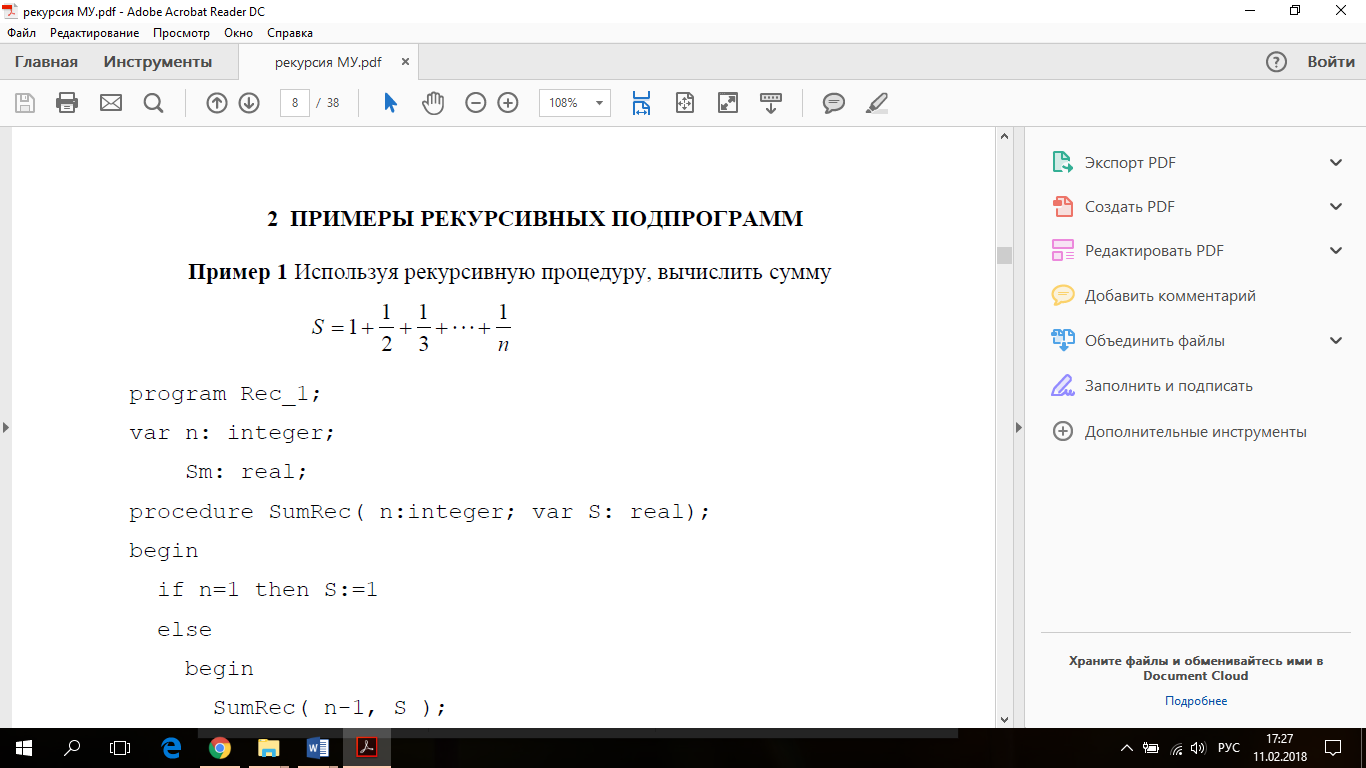
program Rec_1;

var n: integer;

Sm: real;

procedureSumRec( n:integer; var S: real);

begin

if n=1 then S:=1

else begin SumRec( n-1, S );

S:=S+1/n

end

end;

begin // основная

write('n=');

readln (n);

SumRec( n, Sm );

writeln('Сумма =',Sm:10:8)

end.

Результат:

n=5

Сумма =2.28333333

Задача 2: Вывести на печать введенные символы , но в обратном порядке ( с выполнением действий как на рекурсивном спуске, так и на рекурсивном возврате)

Program revers_string;

var n,s:integer;

//st:string;

ProcedureRevers;

Var ch:char;

Begin

If s<>n then

Begin

Read(ch); спуск( помещение в стек)

s:=s+1;

Revers;

Write(ch); // st:=st+ch; подъём (извлечениеизстека)

End;

Begin//основная

writeln ('введите количество вводимых символов');

readln(n);

Revers;

//Write (st);

End.

Порядок выполнения работы:

Для загрузки интегрированной среды запустите файл - РascalABC.exe.
Создайте новый файл для ввода текста программы: меню Файлà пункт Новый(Ctrl+N) или кнопка на панели инструментов Новый файл.
В окне для ввода текста программы наберите свою программу. После заголовка программы в комментарии напишите условие задания.
Запустите программу на выполнение: меню Программа àпункт Выполнить или кнопка Выполнить на панели инструментов
Сохраните программу: меню Файлàпункт Сохранить какàукажите место сохранения файла и имя файла.àV:\группа\студент\задача _номер

Содержание отчёта:

1. Шифр работы

2. Название работы

3. Цель работы

4. Условие задачи

5. Блок-схема алгоритма

6. Текст программы

Из окна вывода

Исходные данные

Результат решения

Контрольные вопросы

Какой вид имеет структура описания процедуры/функции?
В чем отличия процедуры и функции?
Что такое область действия идентификаторов?
Кикие способы передачи параметров реализованы в языкеPascal?
Какие параметры называются формальными, а какие – фактическими?
Для чего используется процедура exit?
Каковы правила передачи параметров-значений?
Каковы правила передачи параметров-переменных?

Индивидуальные задания:

Часть1:

Вариант № 1.

Даны две матрицы . Напечатать те из них, в которой больше нулевых строк. Использовать подпрограмму, выводящую количество нулевых строк в матрице.

Вариант № 2.

Составить подпрограмму транспонирования квадратной матриц. С её помощью в основной программе транспонировать две матрицы разного размера..

Вариант № 3.

Составить подпрограмму-функцию перевода целого числа из двоичной системы счисления в десятичную. С её помощью перевести массив чисел.

Вариант № 4.

Составить , подпрограмму, которая подсчитывает количество элементов в множестве .

С ее помощью выяснить, в каком из двух множеств больше элементов.

Вариант № 5.

Составить подпрограмму, которая для матрицы создает вектор, элементы которого являются суммой элементов столбца матрицы. В основной программе используя подпрограммы определить максимальную сумму столбца.

Вариант № 6.

Составить подпрограмму, которая выясняет, есть ли в матрице подобные строки (т.е. такие, что каждый элемент одной из строк получен умножением элементов другой строки на некоторую константу). В основной программе из двух матриц вывести ту в которой есть подобные строки.

Вариант № 7.

Составить подпрограмму подсчитывающую количество слов в строке. С её помощью подсчитать общее количество слов в тексте из К строк.

Вариант № 8

Составить подпрограмму, подсчитывающую количество различных цифр в десятичной записи натурального числа N.

Вариант № 9

Составить подпрограмму, печатающую в возрастающем порядке все цифры, не входящие в десятичную запись натурального числа N.

Вариант № 10

Описать подпрограмму вычисления суммы факториалов всех четных чисел от М до К.

Вариант № 11

Описать процедуру, определяющую из даты рождения возраст. Дата рождения задана в формате - хх.хх.хххх.

Вариант № 12

Составить подпрограмму нахождения среднего арифметического элементов побочной диагонали. С её помощью определить в какой из двух матриц среднее арифметическое больше.

Вариант № 13

Составить подпрограмму, которая из массива строк выводит самые длинные.

Вариант № 14

Составить подпрограмму, определяющую в строке процент цифр..

Вариант № 15

Составить подпрограмму, которая удваивает каждую цифру строки.

Вариант № 16

Составить подпрограмму, выводящую цифры, не входящие в заданную строку.

Вариант № 17

Составить подпрограмму, выводящую короткие слова из строки.

Вариант № 18

Составить подпрограмму, выясняющую, является ли целое число простым. С её помощью в основной программе подсчитать количество простых чисел в массиве.

Вариант № 19

Составить подпрограмму которая переставляет строку с максимальным элементом на главной диагонали со строкой с заданным номером ( если эти номера не совпадают).

В основной программе обработать две произвольные матрицы. Для ввода и вывода матриц использовать подпрограммы.

Вариант № 20

Составит подпрограмму-функцию , которая в строке находит позицию его первого символа, не являющегося буквой. С её помощью в основной программе определить в какой из двух строк этот символ встречается раньше.

Вариант № 21

Составить подпрограмму-функцию, которая для трёх чисел а, в и с выясняет, можно ли построить треугольник по трем его сторонам.

1, если можно

К= 0, если нельзя

С её помощью в основной программе обработать два набора значений: а1,в1 , с1 и а2,в2,с2.

Вариант № 22

Составить подпрограмму, которая в целочисленной квадратной матрице находит максимальный элемент заштрихованной области. С её помощью в основной программе обработать две матрицы разного размера.

Вариант № 23

Составить подпрограмму-функцию, которая проверяет заданный массив из Х чисел на упорядоченность по возрастанию. С её помощью в основной программе обработать два массива и тот, который из них неупорядочен обнулить с помощью другой подпрограммы.

Вариант № 24

Составить подпрограмму которая выделяет в тексте первую последовательность цифр и преобразует её в число. С её помощью в основной программе обработать два текста.

Вариант № 25

Дан массив строк. Составить подпрограмму которая сортирует первые N элементов этого массива по возрастанию текущих длин строк.

Вариант № 26

Составить которая для заданной строки формирует строку символов, которые не являются буквой или цифрой и распечатывает эту строку в машинном алфавите. С её помощью в основной программе обработать массив строк.

Вариант № 27

Составить подпрограмму которая в строке удаляет все знаки препинания и подсчитывает их количество. С её помощью в основной программе подсчитать суммарное количество удаленных знаков препинания в массиве из Х строк.

Вариант № 28

Составить подпрограмму которая осуществляет циклический сдвиг элементов массива на один вправо. С её помощью в основной программе осуществить двухкратный сдвиг вправо массива символов.

Вариант № 30

Составить подпрограмму которая для заданной строки получает строку, литеры которой расположены в обратном порядке. (например: было - ‘он дал’, стало - ‘лад но’)

Вариант №31

Составить подпрограмму которая в строке удаляет все символы, не являющиеся буквами и заменяет каждую заглавную букву на строчную. С её помощью в основной программе обработать массив строк.

Вариант № 32

Составить подпрограмму которая в массиве с четным количеством элементов меняет местами соседние элементы: 1 ßà2, 3ßà4, и т.д. . С её помощью в основной программе обработать два массива разной длины.

Вариант № 33

Составить подпрограмму , подсчитывающую сумму цифр целого числа. С её помощью в основной программе найти в строке первое по порядку число с максимальной суммой цифр.

Вариант № 34

Составить подпрограмму, которая в целочисленной квадратной матрице находит минимальный элемент заштрихованной области. С её помощью в основной программе обработать две матрицы разного размера.

Вариант № 35

Составить подпрограмму которая в строке удаляет лишние пробелы, оставляя по одному. С её помощью в тексте из Х строк удалить лишние пробелы и подсчитать их общее количество.

Вариант № 36

Составить подпрограмму которая удаляет i-ый элемент массива, корректируя длину массива. С её помощью в основной программе удалить 2 элемента с позиции i.

Вариант № 37

Составить подпрограмму которая выделяет в строке второе слово и помещает его в конец другой строки. Если такого слова нет, то вывести сообщение.

Вариант № 38

Составить подпрограмму которая проверяет сбалансированность скобок в строке. Скобки

считаются сбалансированными, если открытая скобка стоит перед закрытой и количество совпадает. С её помощью в основной программе обработать две строки.

Вариант № 39

Составить подпрограмму которая определяет процент вхождения каждого символа строки в эту строку.

Вариант № 40

Составить подпрограмму которая поэлементно сравнивает две строки и определяет позицию первого несовпадающего символа.

i, если строки не совпадают

К= 0, если строки совпадают

С её помощью в основной программе обработать два текста и они не совпадают, то с помощью другой подпрограммы скопировать первую строку в конец второй.

Вариант № 41

Составить подпрограмму, которая вводит две строки S1 bS2 и выводит S3 , содержащий литеры присутствующие (по крайней мере однократно) в обеих строках.

(Например, S1= ‘молоко’, S=’кромка’, S=’ком’)

Вариант № 42

Составить подпрограмму, которая по дате , заданной в формате «чч/мм/гг» выдает дату в формате «месяц день год», считая , что все даты относятся к ХХ веку.

(Например: было – ‘11/04/88’, стало - ‘апрель 11 1988’. Используя п/п обработать массив дат.

Вариант № 43

Составить подпрограмму, которая печатает в убывающем порядке все цифры, не входящие в десятичную запись натурального числа. В основной программ обработать с помощью подпрограммы два произвольных числа.

Вариант № 44

Составить подпрограмму, которая в массиве подсчитывает максимальное количество стоящих подряд нулей. .В основной программ обработать с помощью подпрограммы

два произвольных массива.

Вариант № 45

Составить подпрограмму, которая подсчитывает с строке количество гласных букв, находящихся между первым и вторым двоеточием. Если второго двоеточия нет, то подсчитать количество гласных букв от первого двоеточия до конца строки. .В основной программ обработать с помощью подпрограммы две строки.

Вариант № 46

Вариант № 47

Вариант № 48. В основной программ обработать с помощью подпрограммы

определяет, является ли квадратная матрица симметричной относительно главной диагонали. В основной программ обработать с помощью подпрограммы

две матрицы. Для ввода и вывода матриц использовать подпрограммы.

Вариант № 49

Составить подпрограмму-функцию вычисления площади треугольника по координатам его вершин. В основной программе определить в каком из двух треугольников площадь больше.

Вариант № 50

Составить подпрограмму, которая выясняет, имеются ли в массиве повторяющиеся элементы ( если да , то к=1, иначе к-0). С её помощью обработать два массива.

Часть 2: Рекурсия

1) , где k – целая константа

2)Вычислить , где a и n – целые положительные числа

3)Вычислить сумму первых n членов чисел Фибоначи.

Числа Фибоначи: 1, 1, 2, 3, 5, 8, 13, 21, 34,55 ….

4)Составить рекурсивную программу перевода десятичного числа в двоичную систему

5)Дано натуральное число n. Вычислить

6)Вычислить

x = 2 ( ( x2 ) 2 ) 2 = 162 = 256

7)Вычислить

x = 3 ( ( x2 ) 2 ) 2 = 812 = 6561

8)Даны действительное число а и натуральное число п. Вычислить

Р = а(а - n)(а – 2n)... (а - n²)

9)Дано натуральное число N. Вычислить произведение первых

N сомножителей

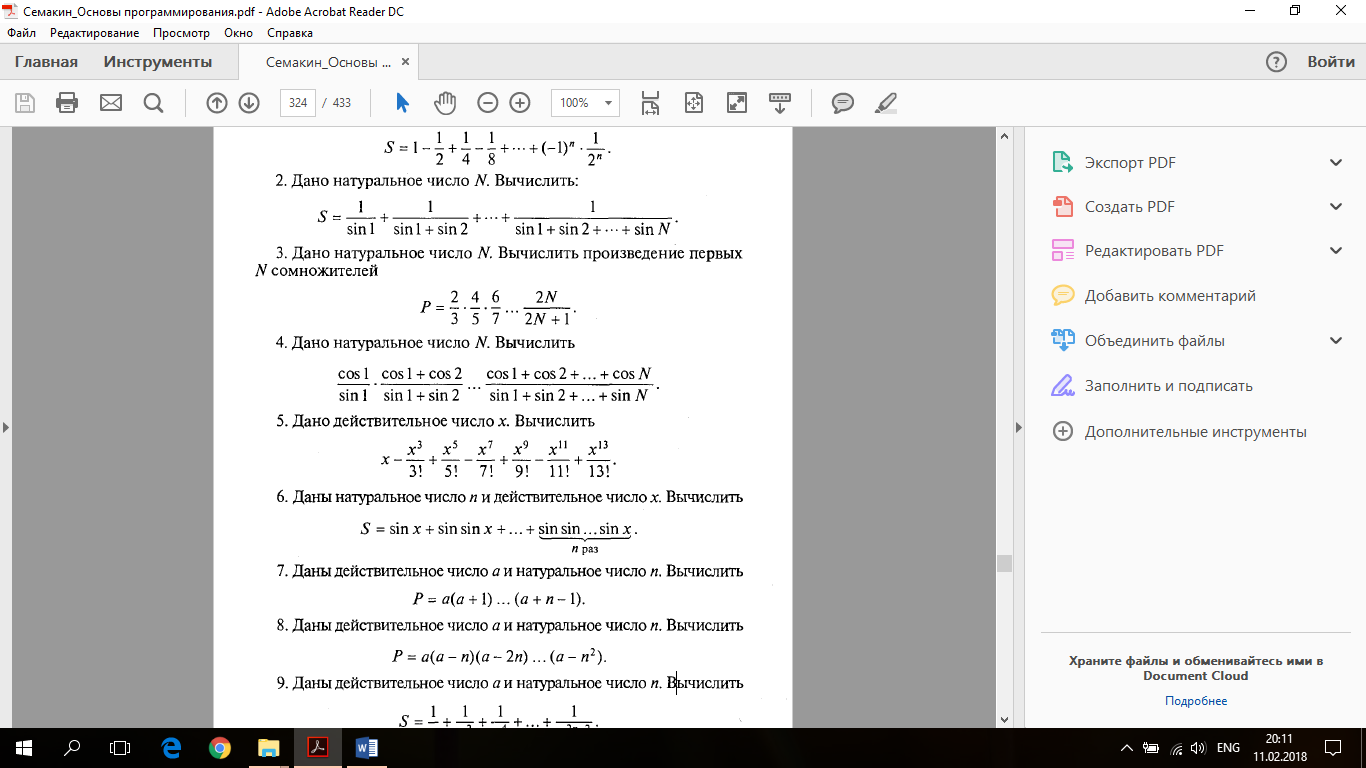
10)Дано действительное число x. Вычислить

11)Дано натуральное число n. Вычислить

12)Дано натуральное число n. Вычислить

13)Дано натуральное число n. Вычислить

14)Дано натуральное число n. Вычислить

15)Дано натуральное число n. Вычислить

16)Описать рекурсивную функцию вычисления

значения по формуле:

17)Описать рекурсивную функцию, которая определяет, является ли заданное

натуральное число простым. Используя эту функцию вывести все простые

числа на заданном интервале [a, b].

10)Вводится с клавиатуры последовательность из n символов – цифр. Описать рекурсивную функцию, которая превращает последовательность символов в целое число. Использовать функцию для вычисления нескольких чисел с различным количеством значащих цифр.

11) Описать рекурсивную функцию вычисления значения по

формуле: