Связь графиков функции и производной
Производная характеризует скорость изменения функции Если функция возрастает – производная положительна (касательная наклонена вправо) Если функция убывает – производная отрицательна (касательная наклонена влево) Если функция имеет максимум или минимум, либо «точку перегиба» - производная равна нулю (касательная лежит горизонтально) Чем больше скорость возрастания (или убывания) функции, тем больше по модулю производная, и тем круче (ближе к вертикали) наклон касательной В точках А и D функция возрастает – производная положительна. В точке А наклон касательной круче, значит, и производная больше, чем в точке D. В точках В и С функция убывает – производная отрицательны. В точке В функция наклон касательной круче, значит, производная меньше, чем в точке C (ПО МОДУЛЮ – больше)
Геометрический смысл производной
Производная – это тангенс угла наклона касательной (или угловой коэффициент касательной)
| Как найти угловой коэффициент касательной (или производную) | Пример: На рисунке изображены график функции  и касательная к нему в точке с абсциссой  . Найдите значение производной функции  в точке .
| 
| ||
| 1. Найти точки на линии касательной, которые точно попадают в пересечение клеточек (обычно на рисунке эти точки отмечены). 2. Через одну из точек провести горизонтальную линию, через другую – вертикальную. Получится треугольник. 3. Сосчитать (в клеточках) длины вертикальной и горизонтальной сторон треугольника. Разделить длину вертикалной стороны на длину горизонтальной 4. Если наклон касательной вправо («подъем») – ставим знак «плюс», если наклон влево («спуск») – ставим знак «минус» |
| |||
| Ответ: Значение производной в точке х0 равно 0,25 | ||||
Здесь «подъем», знак «плюс».
Нахождение точек, где касательная параллельна прямой
Если требуется определить точки, где касательная параллельна прямой 
, то надо искать точки, где производная равна k (числу перед иксом). А если касательная должна быть параллельна прямой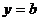 
(или оси абсцисс), то производная должна быть равна 0)
| Пример: Дан график производной функции f(x). Указать количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=x Решение: для прямой y=x угловой коэффициент равен 1, значит, производная должна быть равна 1. Таких точек на графике две. |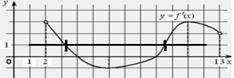 
|
Физический смысл производной
- Если функцией является перемещение тела, то произвозная от этой функции – скорость
- Если функцией является скорость, то производная от этой функции – ускорение
Пример: Материальная точка движется по закону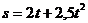 
. Найти мгновенную скорость в момент 
Скорость v – производная от перемещения s: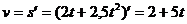 
. При t=5 
Связь графиков функции и производной
| Производная | Функция | Касательная к графику функции |
| Положительна | Возрастает | Наклонена вправо (острый угол с осью Х) |
| Отрицательна | Убывает | Наклонена влево (тупой угол с осью Х) |
| Равна нулю (с вариантами) | Стационарная точка | Горизонтальна (параллельна оси Х) |
| =0, меняет знак с мИнуса на плюс | Минимум (экстремум) | |
| =0, меняет знак с плюСа на минус | МакСимум (экстремум) | |
| =0, но знак не меняет | Точка перегиба |
Дата добавления: 2018-06-01; просмотров: 4736; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!