Расчет сечения нижней части колонны

Стр 1 из 2Следующая ⇒

Расчет и конструирование колонн производственных зданий

Расчет и конструирование надкрановой части внецентренно сжатой колонны сплошного сечения.

Согласно приложению И1 для определения расчетных длин вычисляем:

F₂ =101,889-20,700-11,595·0,9=70,754 т

F₁ = 20,700+11,595·0,9=31,136 т – сумма нагрузок в сечении 1-1.

Отношение принимаем 0,1

По таблице И.3 СП 16.13330.2011 интерполяцией определяем коэффициент

Коэффициент расчетной длины μ₂:

μ₂ = μ₁/α₁ = 2,24/0,525= 4,27>3

Принимаем μ₂ = 3

Расчетная длина участков колонны:

в плоскости действия момента

l_x₁ = μ₁·l₁= 2,24 ·12,58 = 28,18 м

l_x₂ = μ₂·l₂ = 3 · 3,82 =11,46 м

из плоскости действия момента

l_у1 = l₁=12,58 м

l_е_fy2 = 3,82 -0,60 = 3,22 м – из Н_t вычитаем высоту подкрановой балки.

Расчет верхней части колонны

Для колонны принимаем сталь С 255 с R_у = 2400 кг/см².

При: N₂ =40,662т = 40662 кг;

М₂ = -13,293 т^.м = 13293 кг^.м

Предварительно находим значения:

е = М₂/N₂ =13,293/40,662 = 0,326 м = 32,6 см

i_x = 0,42·h₁ = 0,42·45 = 18,9 см

ρ_x ≈ 0,35·h₁ = 0,35· 45 = 15,75 см

λ_х = l_x₂/ i_x = 11,46/0,189=60,6

Условная гибкость стержня

Относительный эксцентриситет

m = e/ρ_х = 32,6/15,75= 2,07< 5

Коэффициент влияния формы сечения табл. Д.2 [СП 16.13330.2011]

η = (1,9 - 0,1m) - 0,02·(6 - m)·λ_х = (1,9 – 0,1·2,07) – 0,02·(6 –2,07)·2,07 = 1,86

Приведенный относительный эксцентриситет (п. 9.22 [1])

m_ef = η·m =1,86 · 2,07 = 3,85

При m_ef = 3,85 и λ_ef =2,07 по интерполяции вычисляем φ_е = 0,265 (табл. Д.3 [1])

Требуемая площадь сечения

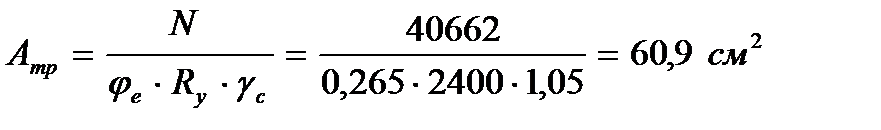
Намечаем минимальную ширину сечения колонны

Принимаем

A_w =

A_f_,тр = 0,5 (A_тр - A_w) = 0,5 ∙ (60,9 – 25,8) = 17,6 см²

Ширина полки:

- из условия обеспечения устойчивости в плоскости действия момента:

- из условия обеспечения местной устойчивости полки, согласно п. 7.3.6 и табл. 10[1]:

- из условия обеспечения устойчивости колонны из плоскости действия момента:

16,1÷10,7 см

b_f₁= 17,6 см <b_f<b_f₂=15,1 см

b_f≥ b_f₃=16,1 см

Условие не выполняется.

Принимаем

A_w =

A_f_,тр = 0,5 (A_тр - A_w) = 0,5 (60,9 – 25,6) = 17,7 см²

Ширина полки:

- из условия обеспечения устойчивости в плоскости действия момента:

- из условия обеспечения местной устойчивости полки:

- из условия обеспечения устойчивости колонны из плоскости действия момента:

16,1÷10,7 см

b_f₁= 14,8 см <b_f<b_f₂=18,1 см

b_f≥ b_f₃=16,1 см

Условие выполняется

Принимаемb_f =18,0 см, при t_f= 1,2 см и h_w =42,6 см, при t_w= 0,6 см

Фактическая площадь сечения надкрановой части колонны:

А = 42,6·0,6+2·18·1,2 = 68,8см²

После назначения размеров полок и стенки сечения колонны вычисляем фактические значения: J_x, J_y,W_x, i_x, i_y, ρ, λ_x, m и m_ef, а затем проверяем расчетное напряжение σ, которое не должно превосходить расчетное сопротивление стали R_y, последовательно определяем:

моменты инерции

момент сопротивления

радиусы инерции и гибкости

Проверяем устойчивость верхней части колонны в плоскости действия момента

По табл. Д2 [1] определяем коэффициент влияния формы сечения ηпри:

При А_f/A_w=0,5:

При А_f/A_w≥ 1,0:

Интерполяцией находим коэффициент η при А_f/A_w=0,798:

А_f/A_w=0,5 → η=1,42;

А_f/A_w=1,0 → η=1,53;

∆А_f/A_w=0,5 → ∆ η=0,11;

m_ef= η∙m_х= 1,5∙2,05 = 3,08

По табл. Д.3 СП 16.13330.2011 интерполяцией определяем коэффициент φ_е:

При λ_х = 2,07 и m_ef= 3,08 → φ_е= 0,307

Фактическое напряжение в сечении

Проверяем устойчивость из плоскости действия момента

По таблице Д.1 приложения Д (СП 16.13330.2011) определяем коэффициент устойчивости при центральном сжатии φ. По таблице 7 (СП 16.13330.2011) определяем тип сечения – b.

Тогда: при 2,6φ= 0,722

при 2,8φ = 0,683

при ∆φ = 0,039

при 2,67

При М_в = 0,

Условие выполнено.

Проверяем местную устойчивость стенки согласно п. 9.4.2. и табл. 22 СП 16.13330.2011:

Для определения предельной условной гибкости необходимо определить следующие параметры:

Исходя из этого, предельную условную гибкость необходимо определять по формуле 126 таблицы 22 СП 16.13330.2011.

- условие не выполняется.

Согласно п. 9.4.3 СП 16.13330.2011 предельную условную гибкость ,вычисленную по формулам (125) и (126)таблицы 22, допускается увеличивать путем определения ее по формуле

гдезначение , вычисляется по формулам (125), (126), а значение , вычисляется по формуле(127)таблицы 22.

При этом должно выполняться условие:

Для проверки данного условия определяем следующие параметры:

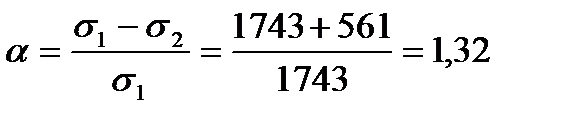
Так как условие выполняется, то:

- то предельная условная гибкость принимаем равной

Тогда:

- условие выполнено, значит,местная устойчивость стенки обеспечена.

Расчет сечения нижней части колонны

Предварительно задаемся типом сечения нижней части колонны. Шатровую ветвь принимаем из уголков и листа, а подкрановую из двутавра. Ветви соединяются решеткой из одиночных уголков, располагаемых под углом 45 – 50 ⁰ к горизонтали. Высоту сечения ранее приняли h₂=1,5м

z₁ – расстояние от центра тяжести сечения колонны до ветви, противоположной рассматриваемой (в несимметричных сечениях z₁ = (0,4…0,5)∙h – до наиболее нагруженной ветви).

z₁ = 0,5·h₂ = 0,5·1,5 = 0,75 м

z₂ = h₂ – z₁ = 1,5 – 0,75 = 0,75 м

Определяем максимальное усилие в ветвях

Для расчета подкрановой ветви

Сечение 3 – 3

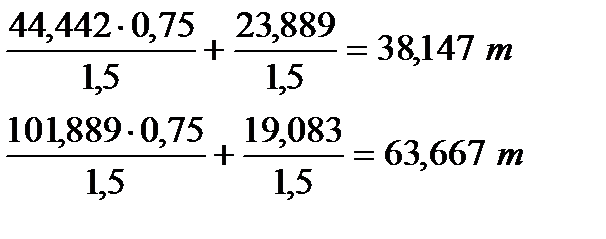
Сечение 4 – 4

Для расчета наружной ветви

Сечение 3 – 3

Сечение 4 – 4

Принимаем:

- для расчета подкрановой ветви 80,418 т = 80418 кг

- для расчета шатровой ветви 101,176 т = 101176 кг

Расчет подкрановой ветви

При l_y₁ = l₁ = 1258см

Высота двутавра назначается в пределах (1/20…1/30)∙l₁ = (1/20…1/30)∙1258=62,9…41,9 см,

Назначаем двутавр № 36 с характеристиками:

А = 61,9см²; i_x = 14,7см; i_y = 2,89см; b_f = 145 мм; h = 360мм

J_x = 13380см⁴; J_y = 516см⁴; W_x = 743см³;

Определяем гибкость подкрановой ветви:

Определяем предельную гибкость. Так как , то:

Тогда: при 2,8φ = 0,683

при 3,0φ = 0,643

при ∆φ = 0,040

при 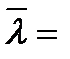2,92

Проверяем устойчивость ветви

, условие выполняется.

Запас прочности большой, уменьшаем площадь поперечного сечения двутавра.

Назначаем двутавр №33 с характеристиками:

А = 53,8см²; i_x = 13,5см; i_y = 2,79см;

J_x = 9840см⁴; J_y = 419см⁴; W_x = 597см³;

Гибкость

Определяем предельную гибкость:

при 3,0φ = 0,643

при 3,2φ = 0,602

при ∆φ = 0,041

при 3,18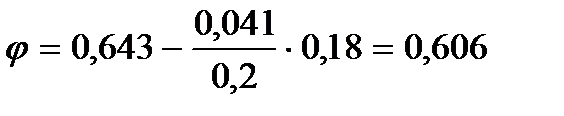

Проверяем устойчивость ветви

, условие выполняется.

Расчет наружной ветви

Задаемся гибкостью λ_х = 60. Определяем предельную гибкость:

при 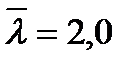φ = 0,744

при φ = 0,709

при ∆φ = 0,035

при

Ориентировочная площадь сечения наружной ветви:

Принимаем b_л = h – 40мм = 330-40 = 290мм

Назначаем толщину листа от 10 до 20 мм, кратно 2 мм: t_л = 10 мм

Требуемая площадь уголка:

Проектируем сечение из двух уголков ∟125х12листа t_л = 10 мм

А_уг = 28,9см²; i_x = 3,82см;

J_x =422 см⁴; z_o = 3,53 см;

Фактическая площадь наружной ветви:

А_нв =1,0·29+28,9·2 = 86,8 см².

Общая площадь сечения

Σ А = А_пв + A_нв = 53,8 + 86,8 = 140,6 см²

Расстояние от наружной грани шатровой ветви до центра ее тяжести:

Расстояние от центра тяжести всего сечения до центра тяжести ветвей:

Уточняем усилия в ветвях

Гибкость подкрановой ветви

Определяем предельную гибкость:

при 3,0φ = 0,643

при 3,2φ = 0,602

при ∆φ = 0,041

при 3,18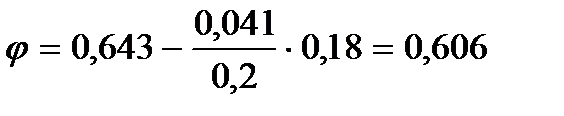

Напряжение в сечении двутавра № 33

Проверка выполняется.

Момент инерции наружной ветви из плоскости действия момента:

Момент инерции наружной ветви в плоскости действия момента:

Определяем радиус инерции наружной ветви колонны из плоскости действия момента:

То же, в плоскости действия момента:

Гибкость всей ветви:

Гибкость ветви между узлами решетки:

Определяем предельную гибкость:

при 3,4φ = 0,562

при 3,6φ = 0,524

при ∆φ = 0,038

при 3,55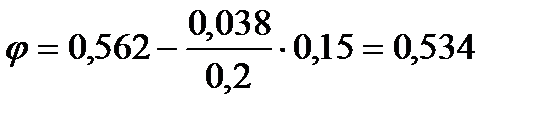

Напряжение в сечении наружной ветви:

, условие выполняется.

Геометрические характеристики всего сечения колонны:

Гибкость нижней части колонны

Принимаем предварительно раскосы из уголков 70х5мм: А_d = 6,86см²; i_min= 2,16см.

А_d1 = 2·A_d = 2·6,86 = 13,72см² – площадь сечения раскосов по двум граням сечения колонны.

Определяем приведенную гибкость по формуле 15 табл.8 [1]:

где α = 28 при α = 45 ⁰;

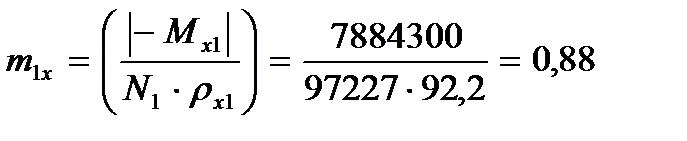
По табл. Д.4приложения Д (СП 16.13330.2011) определяем

при m₁_x = 0,88 и = 1,46 находим φ_e1 = 0,487

при m₂_x = 2,58 и = 1,46 находим φ_e2 = 0,267

Проверяем устойчивость колонны

- условие выполняется.

-условие выполняется.

Дата добавления: 2018-06-01; просмотров: 452; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!