Полученный регрессионный анализ

Рис.2 Нормальный вероятностный график

 

 

Таблица №5

Предсказанные значения и остатки

Зависимая перемен.: P2O5

	Наблюд. Значение	Предск. Значение	Остатки	Станд. предск.	Станд. Остатки	Стд.Ош. предск.	Махалан. расст.	Удален. остатки	Кука расст.
1	0,10	0,05	0,05	-0,43	1,34	0,01	0,19	0,05	0,03
2	0,09	0,05	0,04	-0,48	1,08	0,01	0,23	0,04	0,02
3	0,08	0,05	0,03	-0,48	0,80	0,01	0,23	0,03	0,01
4	0,04	0,05	-0,01	-0,54	-0,27	0,01	0,29	-0,01	0,00
5	0,09	0,05	0,04	-0,49	1,08	0,01	0,24	0,04	0,02
6	0,10	0,05	0,05	-0,32	1,32	0,01	0,10	0,05	0,03
7	0,05	0,08	-0,03	3,79	-0,70	0,03	14,34	-0,05	0,40
8	0,08	0,06	0,02	0,42	0,66	0,01	0,17	0,03	0,01
9	0,05	0,05	0,00	-0,41	-0,02	0,01	0,16	0,00	0,00
10	0,05	0,05	0,00	-0,49	-0,01	0,01	0,24	0,00	0,00
11	0,01	0,05	-0,04	-0,54	-1,09	0,01	0,29	-0,04	0,02
12	0,00	0,05	-0,05	-0,52	-1,36	0,01	0,27	-0,05	0,04
13	0,13	0,05	0,08	-0,50	2,17	0,01	0,25	0,08	0,09
14	0,07	0,06	0,01	1,02	0,29	0,01	1,04	0,01	0,00
15	0,04	0,05	-0,01	-0,57	-0,27	0,01	0,32	-0,01	0,00
16	0,02	0,05	-0,03	-0,57	-0,81	0,01	0,33	-0,03	0,01
17	0,07	0,07	0,00	1,99	0,13	0,01	3,96	0,01	0,00
18	0,02	0,05	-0,03	-0,60	-0,81	0,01	0,36	-0,03	0,01
19	0,10	0,06	0,04	1,77	0,98	0,01	3,13	0,04	0,08
20	0,03	0,05	-0,02	-0,56	-0,54	0,01	0,32	-0,02	0,01
21	0,09	0,05	0,04	0,05	0,99	0,01	0,00	0,04	0,02
22	0,09	0,06	0,03	0,53	0,91	0,01	0,28	0,03	0,02
23	0,03	0,05	-0,02	-0,47	-0,55	0,01	0,22	-0,02	0,01
24	0,11	0,05	0,06	-0,46	1,62	0,01	0,21	0,06	0,05
25	0,02	0,05	-0,03	-0,58	-0,81	0,01	0,34	-0,03	0,01
26	0,02	0,06	-0,04	0,97	-1,06	0,01	0,95	-0,04	0,04
27	0,00	0,05	-0,05	-0,55	-1,36	0,01	0,30	-0,05	0,04
28	0,01	0,05	-0,04	-0,64	-1,07	0,01	0,41	-0,04	0,03
29	0,01	0,05	-0,04	-0,69	-1,06	0,01	0,48	-0,04	0,03
30	0,03	0,06	-0,03	1,63	-0,90	0,01	2,67	-0,04	0,06
31	0,00	0,05	-0,05	-0,60	-1,35	0,01	0,36	-0,05	0,04
32	0,04	0,05	-0,01	-0,31	-0,31	0,01	0,10	-0,01	0,00
33	0,08	0,05	0,03	-0,46	0,80	0,01	0,21	0,03	0,01
34	0,06	0,05	0,01	0,09	0,17	0,01	0,01	0,01	0,00
Минимум	0,00	0,05	-0,05	-0,69	-1,36	0,01	0,00	-0,05	0,00
Максим.	0,13	0,08	0,08	3,79	2,17	0,03	14,34	0,08	0,40
Среднее	0,05	0,05	0,00	0,00	0,00	0,01	0,97	0,00	0,03
Медиана	0,05	0,05	-0,01	-0,48	-0,14	0,01	0,28	-0,01	0,02

 

Нелинейная регрессия

 

Различают два класса нелинейных регрессий:

§ регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

§ регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:

§ полиномы разных степеней:

§ равносторонняя гипербола: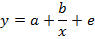  

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

§ степенная:                               

§ показательная:                       

§ экспоненциальная:                

Параметры нелинейной регрессии по включенным переменным оцениваются, как и в линейной регрессии, методом наименьших квадратов, поскольку эти функции линейны по параметрам.

Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.

Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем к нулю первую производную параболы второй степени. Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.

Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу:

Иначе обстоит дело с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях широко используется степенная функция:

Данная модель нелинейна относительно оцениваемых параметров, ибо включает параметры и неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду. Соответственно оценки параметров и могут быть найдены с помощью МНК.

В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель , поскольку логарифмируя ее по натуральному основанию, получим линейную форму модели: .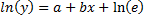

Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

 

 

Кластерный анализ

 

Кластерный анализ — это общий термин для целого ряда методов, используемых для группировки объектов, событий или индивидов в классы (кластеры) на основе сходства их характерных признаков. Несмотря на отсутствие единого определения кластера, во всех его определениях особо подчеркиваются такие условия, как сходство, однородность и близость. Если воспользоваться специальной терминологией, то кластеры можно определить, как однородные подгруппы, формируемые методом, который минимизирует дисперсию внутри групп (кластеров) и максимизирует дисперсию между группами.

Методики кластеризации используются для установления сходных подгрупп объектов или индивидов и для построения таксономии. Таким образом, они помогают исследователю в описании структуры совокупности объектов и отношений между ними, а также в формулировании законов и утверждений относительно классов объектов.

Если обобщить различные классификации методов кластеризации, то можно выделить ряд групп (некоторые методы можно отнести сразу к нескольким группам и потому предлагается рассматривать данную типизацию как некоторое приближение к реальной классификации методов кластеризации):[1]

Вероятностный подход. Предполагается, что каждый рассматриваемый объект относится к одному из k классов.

K-средних (K-means)

K-medians

EM-алгоритм

Алгоритмы семейства FOREL

Дискриминантный анализ

Подходы на основе систем искусственного интеллекта.

Весьма условная группа, так как методов AI очень много и методически они весьма различны.

Метод нечеткой кластеризации C-средних (C-means)

Нейронная сеть Кохонена

Генетический алгоритм

Логический подход. Построение дендрограммы осуществляется с помощью дерева решений.

Теоретико-графовый подход.

Графовые алгоритмы кластеризации

Иерархический подход. Предполагается наличие вложенных групп (кластеров различного порядка). Алгоритмы в свою очередь подразделяются на агломеративные (объединительные) и дивизивные (разделяющие). По количеству признаков иногда выделяют монотетические и политетические методы классификации.

Иерархическая дивизивная кластеризация или таксономия. Задачи кластеризации рассматриваются в количественной таксономии.

---

Дата добавления: 2018-06-27; просмотров: 350; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!