Оптимальный выбор в условиях противоборства: теория игр в задачах принятия решений

⇐ ПредыдущаяСтр 9 из 17Следующая ⇒

Теория игр помогает вырабатывать оптимальные управленческие решения в ситуациях игрового характера. Формализуя конкретные ситуации математически, их можно представить как игру двух или более игроков, каждый из которых преследует цель максимизации своей выгоды, своего выигрыша за счет другого.

Решение подобных задач требует определенности в формировании их условий: установления количества "игроков" и правил игры, выявления возможных стратегий игроков, возможных выигрышей (отрицательный выигрыш понимается как проигрыш). Важным элементом в условии задачи является стратегия, т.е. совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор данного игрока. Количество стратегий у каждого игрока может быть конечным и бесконечным, отсюда и игры подразделяются на конечные и бесконечные. При исследовании конечных игр задаются матрицы выигрышей, а при бесконечных – функции выигрышей. Для решения задач применяются алгебраические методы, основанные на системе линейных уравнений и неравенств, итерационные методы, а также сведение задачи к некоторой системе дифференциальных уравнений.

При принятии решения для игровой ситуации составляется матрица игры, содержащая выигрыши a_ij игрока, выбравшего i-ю стратегию при j-м состоянии рыночной среды (Природы).

a₁₁	a₁₂	p₁	Нижнюю цену игры находят из выражения a = max_i min_j a_ij .
a₂₁	a₂₂	p₂	Затем определяют верхнюю цену игры b = min_j max_i a_ij .

Если нижняя цена игры не равна верхней, т.е. a ¹ b, тогда решение игры находят в смешанных стратегиях. В этом случае вероятности применения различных стратегий р₁ и р₂ в игре два на два (2 х 2) и цену игры V определяют исходя из следующих соотношений.

а₁₁ _* р₁ + а_{21 *} р₂ = V ;

а₁₂ _* р₁ + а_{22 *} р₂ = V ;

р₁ + р₂ = 1.

; р₂ ₌ 1 – р₁ ; .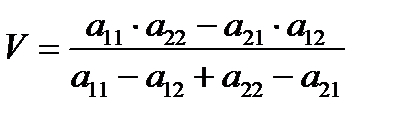

Пример. Допустим, руководство предприятия рассматривает два альтернативных варианта решения (А₁ и А₂) при двух возможных сценариях (В₁ и В₂) развития ситуации во внешней среде. Оценки последствий решений в виде ожидаемой прибыли (в млн. ден.ед) представлены следующей матрицей игры

	В₁	В₂
А₁	5	3
А₂	1	7

Определим нижнюю a и верхнюю β цену игры:

	В₁	В₂	a_i = min_j a_ij
А₁	5	3	3	a = max_i a_i
А₂	1	7	1
β_j = max_i a_ij	5	7
	β = min_j β_j			a ¹ β

Поскольку нижняя цена игры не равняется верхней, игра решается в смешанных стратегиях.

р₂ ₌ 1 – р₁ = 1 – 0,75 = 0,25

Таким образом, для получения гарантированной прибыли, равной 4 млн. ден.ед., необходимо чередовать возможные решения с частотой ( вероятностью) 0,75 для С₁ и 0,25 для С₂. Или распределить свои ресурсы между решениями С₁ и С₂ в пропорции 3:1 (0,75:0,25 = 3:1).

В игре с Природой решение принимается с учётом полезности возможного результата при различных сценариях развития ситуаций во внешней среде (например, конъюнктура рынка или условия погоды) и оценок их вероятности.

Пусть имеется m возможных стратегий (линий поведения) - С₁, …, С_i,…, С_m ; n состояний Природы П₁, …, П_j,…П_n, оценки вероятности которых равны q₁, …, q_j,…q_n, результат игры а_ij при каждом сочетании стратегий задан матрицей игры:

	П₁	…	П_j	…	П_n
С₁	а₁₁	…	а₁_j	…	а_1n
…	…	…	…	…	…
С_i	а_i₁	…	а_ij	…	а_in
…	…	…	…	…	…
С_m	а_m₁	…	а_mj	…	а_m_n

Необходимо выбрать наилучшую стратегию поведения, которая по сравнению с другими наиболее выгодна.

Допустим, руководство предприятия должно выбрать вариант планового решения об уровне выпуска и реализации продукции с учётом конъюнктуры рынка:

План производства и реализации продукции	Конъюнктура рынка
	П₁	П₂	П₃
	Вероятности состояния спроса
	q₁ = 0,2	q₂ = 0,5	q₃ = 0,3
	Размер прибыли а_ij , млн. ден.ед.
С₁	7,2	8,7	6,5
С₂	8,8	7,3	9,4
С₃	6,4	5,4	7,4

Критерии выбора стратегии

Проведем анализ стратегий производства при неопределенной рыночной конъюнктуре. Для выбора наилучшей стратегии поведения на рынке товаров и услуг существуют различные критерии, среди которых можно назвать критерии: Байеса, Лапласа, Вальда, Сэвиджа, Гурвица и максимакса. Предпочтительнее будет выбрать то решение, которое будет оценено как наиболее полезное по нескольким критериям.

Критерий Байеса используется, если в результате исследований известны вероятности всех состояний Природы (q_j). При этом, если учтены все из n возможных состояний, тогда

= 1.

В этом случае в качестве показателя, который необходимо максимизировать, берется среднее значение выигрыша

B = × q_j.

Определим наилучшую стратегию по критерию Байеса:

7,2 × 0,2 + 8,7 × 0,5 + 6,5 × 0,3 = 7,74 ,

8,8 × 0,2 + 7,3 × 0,5 + 9,4 × 0,3 = 8,23 ,

6,4 × 0,2 + 5,4 × 0,4 + 7,4 × 0,3 = 6,2.

Наилучшая стратегия С₂ дает максимальный средний «выигрыш» в размере 8,23 млн. ден.ед.

Критерий Лапласа применяется в случае наибольшей неопределенности обстановки. При этом все n состояний Природы принимаются равновероятными, т.е. вероятность каждого из состояний q_j = . Согласно этому критерию «недостаточного основания» находится максимальный «средний» выигрыш.

L = .

Определим наилучшую стратегию по критерию Лапласа:

(7,2 + 8,7 + 6,5) /4 = 7,5,

(8,8 + 7,3 + 9,4) /4 = 8,5,

(6,4 + 5,4 + 7,4) /4 = 6,4.

Наилучшая стратегия С₂ дает максимальный средний «выигрыш» в размере 8,5 млн. ден.ед.

Критерий Вальда – это максиминный критерий крайнего пессимизма, или наибольшей осторожности, перестраховки. В этом случае оптимальной гарантированной стратегией для игрока С будет чистая стратегия С_i, при которой наименьший «выигрыш» будет максимальным:

V = а_ij.

Используя матрицу игры, определяем минимальный выигрыш для всех стратегий

a₁ = 6,5; a₂ = 7,3; a₃ = 5,4.

Наилучшая стратегия С₂ даёт максимальный (из минимальных) «выигрыш» в размере 7,3 млн. ден.ед.

Критерий Сэвиджа сводится к тому, чтобы любыми путями избежать большого риска при принятии решения. Оптимальной будет стратегия С_i, при которой минимизируется величина максимального риска в наихудших условиях:

S = r_ij.

Риск рассчитывается как разность между ожидаемым результатом действий при наличии точных данных об обстановке и результатом, который может быть достигнут, если эти данные точно не известны. Величины риска определяются из следующего выражения:

r_ij = а_ij – а_ij = b_j – a_ij,

где а_ij – размер «выигрыша» при выборе i–й стратегии при j–м состоянии Природы; b_j - максимальный «выигрыш» для j–й обстановки; r_ij - величина риска при выборе i–й стратегии при j–й обстановке. Составим матрицу рисков

	П₁	П₂	П₃
С₁	1,6	0	2,9
С₂	0	1,4	0
С₃	2,4	3,3	2

Используя матрицу рисков, находим максимальные риски для всех стратегий

r_i = r_ij

r₁ = 2,9, r₂ = 1,4, r₃ = 3,3.

Наилучшая стратегия С₂ допускает минимальный риск (из максимальных) в размере 1,4 млн. ден.ед.

Критерий Гурвица является линейной комбинацией пессимистической и оптимистической позиций. Стратегия выбирается из условия

G = {k × а_ij + (1 – k) × а_ij},

где k – коэффициент «пессимизма».

Коэффициент k меняется от 0 до 1, не принимая этих граничных значений (0 < k < 1). Коэффициент k выбирается на основании опыта или из субъективных соображений. Чем опаснее ситуация, тем менее мы склонны к риску, тем больше мы хотим подстраховаться, а значит, тем ближе к единице выбирается k. Примем k = 0,4, тогда

0,4 × 6,5 + 0,6 × 8,7 = 7,82,

0,4 × 7,3 + 0,6 × 9,4 = 8,56,

0,4 × 5,4 + 0,6 × 7,4 = 6,6.

Наилучшая стратегия С₂ дает «выигрыш» в размере 8,56 млн. ден.ед. По большинству критериев наилучшей стратегией является С₂.

Критерий крайнего оптимизма (максимакса) предполагает выбор стратегии, при которой из самых больших «выигрышей» для каждой стратегии выбирается наибольший. Этот критерий характерен для легкомысленного руководителя, полагающегося в принятии решений на «авось»:

M = а_ij.

х₁ = 8,7, х₂ = 9,4, х₃ = 7,4.

Наивыгоднейшая стратегия С₂ может дать «выигрыш» в размере 9,4 млн. ден.ед..

Дата добавления: 2018-06-27; просмотров: 281; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Мы поможем в написании ваших работ!